Método deductivo de las ciencias formales: Matemáticas.
De Wikillerato
| (5 ediciones intermedias no se muestran.) | |||
| Línea 30: | Línea 30: | ||
<h5>Estructura de un sistema formal axiomático</h5> | <h5>Estructura de un sistema formal axiomático</h5> | ||
| - | <li>Parte morfológica | + | <ul> |
| + | <li>Parte morfológica | ||
#Un conjunto de componentes primitivos. | #Un conjunto de componentes primitivos. | ||
#Un conjunto de operaciones relativas a tales componentes. | #Un conjunto de operaciones relativas a tales componentes. | ||
#Un conjunto de reglas de formación expresivas de cómo a partir de los componentes primitivos se pueden construir nuevos componentes llamados derivados. | #Un conjunto de reglas de formación expresivas de cómo a partir de los componentes primitivos se pueden construir nuevos componentes llamados derivados. | ||
| - | <li>Parte axiomática | + | <li>Parte axiomática |
#Un conjunto de axiomas. | #Un conjunto de axiomas. | ||
#Un conjunto de definiciones. | #Un conjunto de definiciones. | ||
#Un conjunto de reglas o criterios de deducción. | #Un conjunto de reglas o criterios de deducción. | ||
#Un conjunto de teoremas demostrados, que se basan en los tres conjuntos anteriores. | #Un conjunto de teoremas demostrados, que se basan en los tres conjuntos anteriores. | ||
| + | </ul> | ||
Lo que se refiere a la parte morfológica, lo hemos estudiado en la [[Lógica proposicional]]. En cuanto a la parte axiomática, se han formulado diferentes grupos de axiomas como los de [[Lukasiewicz]], los de [[Frege]] – [[Lukasiewicz]], y los de [[Hilbert]] – [[Ackermann]], que pasamos a exponer. | Lo que se refiere a la parte morfológica, lo hemos estudiado en la [[Lógica proposicional]]. En cuanto a la parte axiomática, se han formulado diferentes grupos de axiomas como los de [[Lukasiewicz]], los de [[Frege]] – [[Lukasiewicz]], y los de [[Hilbert]] – [[Ackermann]], que pasamos a exponer. | ||
| Línea 44: | Línea 46: | ||
<h5>Axiomas</h5> | <h5>Axiomas</h5> | ||
| - | <li><b>A 1:</b> <math>( p \lor p ) \to p</math | + | <ul> |
| - | <li><b>A 2:</b> <math> p \to (p \lor q)</math | + | <li><b>A 1:</b> <math>( p \lor p ) \to p</math> |
| - | <li><b>A 3:</b> <math>(p \lor q) \to q \lor p</math | + | <li><b>A 2:</b> <math> p \to (p \lor q)</math> |
| - | <li><b>A 4:</b> <math>(p \to q) \to [(r \lor p) \to (r \lor q)] </math> </ | + | <li><b>A 3:</b> <math>(p \lor q) \to q \lor p</math> |
| + | <li><b>A 4:</b> <math>(p \to q) \to [(r \lor p) \to (r \lor q)] </math> | ||
| + | </ul> | ||
| Línea 53: | Línea 57: | ||
Tienen como fin establecer el significado de los operadores no primitivos o derivados. | Tienen como fin establecer el significado de los operadores no primitivos o derivados. | ||
| - | <li><b>Df, 1:</b> <math>p \to q = df \bar{p} v q</math | + | <ul> |
| - | <li><b>Df, 2:</b> <math>p \land q = df \overline {\bar p \lor \bar q}</math | + | <li><b>Df, 1:</b> <math>p \to q = df \bar{p} v q</math> |
| - | <li><b>Df. 3:</b> <math>p \underline{\lor } q = df \overline { p \to q} \lor \overline {(q \to p)}</math | + | <li><b>Df, 2:</b> <math>p \land q = df \overline {\bar p \lor \bar q}</math> |
| - | <li><b>Df. 4:</b> <math>p \leftrightarrow q = df (p \to q) \land (q \to p)</math></ | + | <li><b>Df. 3:</b> <math>p \underline{\lor } q = df \overline { p \to q} \lor \overline {(q \to p)}</math> |
| + | <li><b>Df. 4:</b> <math>p \leftrightarrow q = df (p \to q) \land (q \to p)</math> | ||
| + | </ul> | ||
<h5>Criterios de deducción</h5> | <h5>Criterios de deducción</h5> | ||
| - | <li>D 1: A 1, A 2, A 3, A 4 son tesis. | + | <ul> |
| - | <li>D 2: Si <math>p</math> es una tesis y si <math>p \to q</math> es una tesis, entonces <math>q</math> es una tesis (modus ponendo ponens). | + | <li>D 1: A 1, A 2, A 3, A 4 son tesis. |
| - | <li>D 3: Si una expresión lógica es una tesis y sustituimos en ella una proposición atómica por otra cualquiera, el resultado es una tesis. | + | <li>D 2: Si <math>p</math> es una tesis y si <math>p \to q</math> es una tesis, entonces <math>q</math> es una tesis (modus ponendo ponens). |
| - | <li>D 4: Si <math>p \to q</math> es una tesis, y si <math>q \to p</math> es una tesis, entonces <math>q \to r</math> es una tesis. | + | <li>D 3: Si una expresión lógica es una tesis y sustituimos en ella una proposición atómica por otra cualquiera, el resultado es una tesis. |
| - | <li>D 5: Nada es tesis si no es mediante los criterios: D 1, D 2, D 3 y D 4.</ | + | <li>D 4: Si <math>p \to q</math> es una tesis, y si <math>q \to p</math> es una tesis, entonces <math>q \to r</math> es una tesis. |
| + | <li>D 5: Nada es tesis si no es mediante los criterios: D 1, D 2, D 3 y D 4. | ||
| + | </ul> | ||
A partir de estos axiomas, definiciones y criterios de deducción se pueden ir demostrando los teoremas de la [[lógica proposicional]]. Por ejemplo: | A partir de estos axiomas, definiciones y criterios de deducción se pueden ir demostrando los teoremas de la [[lógica proposicional]]. Por ejemplo: | ||
| - | <li>A partir de A 2, D 1, D 3, se obtiene: <math>p \to ( p \lor p)</math> <b> T1.</b | + | <ul> |
| - | <li>A partir de A 1, T 1, D 1, D 4: <math>p \to p</math> <b> T2.</b | + | <li>A partir de A 2, D 1, D 3, se obtiene: <math>p \to ( p \lor p)</math> <b> T1.</b> |
| - | <li>A partir de T 2, Df 1: <math>\overline {p} \lor p</math> <b> T3.</b | + | <li>A partir de A 1, T 1, D 1, D 4: <math>p \to p</math> <b> T2.</b> |
| - | <li>A partir de A 3, D 1, D 3 : <math>(\overline{p} \lor p) \to ( p \lor \overline {p})</math> <b> T4.</b | + | <li>A partir de T 2, Df 1: <math>\overline {p} \lor p</math> <b> T3.</b> |
| - | <li>A partir de T 3, T 4, D 2 : <math>(p \lor \overline {p})</math> <b> T5.</b></ | + | <li>A partir de A 3, D 1, D 3 : <math>(\overline{p} \lor p) \to ( p \lor \overline {p})</math> <b> T4.</b> |
| - | + | <li>A partir de T 3, T 4, D 2 : <math>(p \lor \overline {p})</math> <b> T5.</b> | |
| + | </ul> | ||
En el método matemático no existe un modelo único de sistema formal axiomático para toda la matemática. Cada una de sus partes, –según el organigrama anterior–, tiene su sistema formal axiomático. | En el método matemático no existe un modelo único de sistema formal axiomático para toda la matemática. Cada una de sus partes, –según el organigrama anterior–, tiene su sistema formal axiomático. | ||
| Línea 79: | Línea 88: | ||
Finalmente, para que un conjunto de axiomas esté bien construido tiene que cumplir los siguientes requisitos: | Finalmente, para que un conjunto de axiomas esté bien construido tiene que cumplir los siguientes requisitos: | ||
| - | <li><b>Independencia:</b> Ninguno de los axiomas puede ser deducido o demostrado a partir de los demás. Cada axioma ha de ser independiente. | + | <ul> |
| - | <li><b>Consistencia:</b> Partiendo de los axiomas no debe ser posible demostrar un teorema y la negación del mismo. No se puede demostrar que 3 + 2 sea igual a 5, y que 3 + 2 sea distinto de 5. | + | <li><b>Independencia:</b> Ninguno de los axiomas puede ser deducido o demostrado a partir de los demás. Cada axioma ha de ser independiente. |
| - | <li><b>Completitud:</b> Significa que sobre cualquier proposición del sistema se pueda determinar si es verdadera o es falsa.</ | + | <li><b>Consistencia:</b> Partiendo de los axiomas no debe ser posible demostrar un teorema y la negación del mismo. No se puede demostrar que 3 + 2 sea igual a 5, y que 3 + 2 sea distinto de 5. |
| + | <li><b>Completitud:</b> Significa que sobre cualquier proposición del sistema se pueda determinar si es verdadera o es falsa. | ||
| + | </ul> | ||
Al aplicar estas condiciones necesarias, surgen las <b>limitaciones de los sistemas formales axiomáticos</b>, que fueron descubiertas por el insigne lógico – matemático <b>[[Kurt Gödel]]</b> en 1931. Gödel afirma que en todo sistema formal axiomático, hay <b>proposiciones indecidibles</b> desde el interior del sistema, es decir, que no se puede afirmar si son verdaderas o falsas, dentro de los límites del sistema. (Habría que salirse del sistema y enunciar otros axiomas, pero esto nos llevaría a un proceso indefinido). | Al aplicar estas condiciones necesarias, surgen las <b>limitaciones de los sistemas formales axiomáticos</b>, que fueron descubiertas por el insigne lógico – matemático <b>[[Kurt Gödel]]</b> en 1931. Gödel afirma que en todo sistema formal axiomático, hay <b>proposiciones indecidibles</b> desde el interior del sistema, es decir, que no se puede afirmar si son verdaderas o falsas, dentro de los límites del sistema. (Habría que salirse del sistema y enunciar otros axiomas, pero esto nos llevaría a un proceso indefinido). | ||
| - | Algunos matemáticos consideraron dentro de este tipo de proposiciones algunas que aún no habían sido demostradas como la | + | Algunos matemáticos consideraron dentro de este tipo de proposiciones algunas que aún no habían sido demostradas como la conjetura de [[Christian Goldbach|Goldbach]]. |
Finalmente, podemos preguntarnos, sobre el tipo de conocimiento y la seguridad o certeza que nos proporcionan las matemáticas, ¿son seguras sus conclusiones? | Finalmente, podemos preguntarnos, sobre el tipo de conocimiento y la seguridad o certeza que nos proporcionan las matemáticas, ¿son seguras sus conclusiones? | ||
| Línea 95: | Línea 106: | ||
Las matemáticas, nos ayudan a: | Las matemáticas, nos ayudan a: | ||
| - | <li>Codificar y descifrar la experiencia. Por ejemplo si “Juana y Pepe pueden cortar el césped de su casa trabajando juntos en 4 horas. Si trabajara Juana sola, tardaría 6 horas, ¿cuánto tardaría Pepe si trabajara solo?<br><b>Solución:</b> Juana 6h <math>\to x</math></li> | + | <ul> |
| + | <li>Codificar y descifrar la experiencia. Por ejemplo si “Juana y Pepe pueden cortar el césped de su casa trabajando juntos en 4 horas. Si trabajara Juana sola, tardaría 6 horas, ¿cuánto tardaría Pepe si trabajara solo?<br><b>Solución:</b> Juana 6h <math>\to x</math> | ||
| + | <li>Juana 4h <math>\to 2/3x</math> | ||
| + | <li>Pepe 4h <math>\to 1/3x</math> | ||
| + | Por lo tanto, Pepe 12h <math>\to 3/3x</math> | ||
| + | <li>No engañarnos con nuestros sentidos o intuiciones: Supongamos que una persona rema 2 Km, río arriba y 2Km. río abajo. Esta persona rema a 5Km. por hora en aguas tranquilas. La corriente del río es de 3 Km. por hora, ¿cuánto tiempo tardará?<br><b>Solución:</b> <math>t = s / v</math> | ||
| + | <li><math>t</math> = Tiempo | ||
| + | <li><math>s</math> = Espacio | ||
| + | <li><math>v</math> = Velocidad | ||
| + | </ul> | ||
| + | <u>Río arriba:</u> | ||
| + | <p><math>v = 5 km/h - 3 km/h = 2 km/h</math></p> | ||
| + | |||
| + | <math>s= 2 km/h</math> | ||
| + | |||
| + | <math>t = 2 km / 2 km/h = 1 h</math> | ||
| + | |||
| + | <u>Río abajo:</u> | ||
| + | <p><math>v = 5 km/h + 3 km/h = 8 km/h</math></p> | ||
| + | |||
| + | <math>s= 2 km/h</math> | ||
| + | |||
| + | <math>t = 2 km / 8 km/h = 1/4 h = 15 min</math> | ||
| + | |||
| + | <b>Total</b> = 1h 15min | ||
| + | |||
| + | A esto podemos añadir que las Matemáticas también pueden apreciarse y comprenderse como un sistema separado, un lenguaje independiente, gracias al cual traducimos y organizamos nuestra experiencia para poderla entender y racionalizar. Por eso decimos que <b>las Matemáticas son el lenguaje en el que escribimos la Física</b>. | ||
| + | |||
| + | Los científicos de la naturaleza, físicos o astrónomos, perciben una relación entre los datos que observan y los encajan en algún patrón matemático. [[Kepler]] -el famoso astrónomo que describió el viaje de la tierra alrededor del sol en órbitas elípticas, usando los datos de [[Thycho Brahe]] sobre la órbita de Marte -, observó que los planetas se movían describiendo elipses y atribuyó estas observaciones a un error de observación, pues aún en esa época se explicaban los movimientos de los astros circularmente. Gracias a sus estudios sobre elipses y cónicas y a su admiración por las matemáticas, pudo volver a la antigua idea de la filosofía pitagórica de que la naturaleza estaba escrita en un lenguaje matemático, y enunció sus tres famosas leyes en su obra fundamental, <i><b>La armonía del mundo</b></i>. | ||
| + | |||
| + | En este sentido, afirma <b>[[Bertrand Russell]]</b>: | ||
| + | |||
| + | <i>“Las matemáticas son, creo yo, la principal fuente de nuestra creencia en verdades eternas y exactas. Esto deja pensar que todo razonamiento exacto se aplica a objetos ideales en contraposición a los objetos sensibles…, que el pensamiento es más noble que los sentidos, y que el objeto del pensamiento es más real que los objetos de la percepción sensible”.</i> | ||
| + | |||
| + | Todas estas reflexiones nos llevan a formularnos varias preguntas: ¿Es inventada la matemática, es decir, consiste en un conjunto de convenciones hechas y acordadas?, o, ¿es algo que el ser humano ha descubierto observando el mundo que le rodea? | ||
| + | |||
| + | Si la matemática es pura invención, ¿cómo es que funciona tan bien?, ¿cómo es que sus aplicaciones se cumplen en el mundo exterior? | ||
| + | Si fue descubierta, ¿cómo es que parecen existir tantos sistemas axiomáticos que cumplen con el criterio de la independencia de los axiomas y que no tienen nada que ver con nuestros sentidos? | ||
| + | |||
| + | ¿Cómo se originó la matemática? Podemos contestar ingenuamente que para contar cabras u ovejas, para comerciar y no ser engañados, pero cuando surgieron los números ellos mismos cautivaron la atención y el interés de los científicos. Pitágoras y su escuela mantenían la existencia de una correspondencia biyectiva entre los números y las realidades naturales, hasta que descubrieron los números irracionales como <math>\sqrt{2}</math> , que ya no era fácil relacionar con la experiencia, con los sentidos. | ||
| + | |||
| + | El debate sigue abierto. | ||
| + | |||
| + | El método matemático, del que venimos hablando, queda resumido en el siguiente texto: | ||
| + | |||
| + | <i>“Euclides construyó su geometría, una geometría que resistió el paso de dos mil años, utilizando un método de trabajo especialmente acertado: <b>el método axiomático</b>. Euclides empezaba por enunciar una serie de verdades que le parecían evidentes por sí mismas y que aceptaba sin demostración previa. Por ejemplo que por dos puntos pasa siempre una recta, o que dos rectas no paralelas se cortan siempre en un solo punto. Una vez aceptados estos presupuestos básicos, las únicas reglas del razonamiento le proporcionaban todo lo demás. A partir de los enunciados primitivos, de los axiomas, se iban encadenando una tras otra las deducciones que se desprendían de ellos, eran los teoremas. | ||
| + | Por supuesto, la elección de los axiomas en cierto sentido arbitraria, puede partirse de un cierto conjunto de enunciados o de otro conjunto distinto. Lo que en verdad importa es que se respeten las reglas deductivas y se mantenga el entramado total en toda su complejidad. | ||
| + | |||
| + | El método de trabajo de la matemática moderna es semejante al de Euclides, sólo que más perfecto y acabado. Supongamos que queremos edificar una teoría matemática, por ejemplo la teoría de conjuntos. Empezaremos por definir una serie de axiomas que nos aclaren lo que entendemos por los conjuntos, luego nos pondremos a deducir de acuerdo con las reglas del juego, y ésta será nuestra teoría de conjuntos. Eligiendo los axiomas con cuidado no hay que temer a la antinomias; precisamente los axiomas se pensarán de tal manera que las antinomias no puedan aparecer. Ésta es la ventaja de una teoría formalizada frente a una intuitiva. Lo único que se le pide a este juego lógico es que no nos lleve a contradicciones, es decir, que no podamos probar a la vez, a partir de los axiomas un teorema y su negación. | ||
| + | |||
| + | Un sistema de axiomas es consistente cuando no es posible probar a la vez un teorema y su contrario. El sueño de Fausto de todo matemático es probar que su ciencia está libre de contradicciones, que resiste todos los asaltos, que es consistente. Y no sólo eso, su sueño incluye el que sea completa, es decir, que todo teorema que haya sido o pueda ser pensado sea susceptible de ser probado o refutado. Por desgracia este ambicioso programa, - el programa de Hilbert -, es sólo un sueño. Un sueño del que nos despertó cruelmente en 1931 Kurt Gödel… Gödel probó que se tomaba un conjunto de axiomas lo suficientemente amplio – que contenga los axiomas de la aritmética como mínimo -, no es posible probar, con las armas de deducción del sistema, que tal conjunto sea a la vez consistente y completo. Es decir, que en caso de ser completo, contendría contradicciones. Y en caso de no tener contradicciones, -es decir, en caso de ser consistente – habría siempre teoremas verdaderos que nunca podríamos demostrar. | ||
| + | |||
| + | Gödel ha demostrado en cierto modo las limitaciones de la matemática. Esta no puede probarlo todo; en particular no puede probar su propia consistencia”.</i> | ||
| + | |||
| + | Navarro, J. <i>“La nueva matemática</i>, p. 47 y ss. | ||
| + | |||
| + | |||
| + | |||
| + | [[Category:Filosofía]] | ||
Revisión actual
Tabla de contenidos |
Las Matemáticas
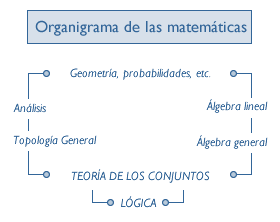
No es tarea fácil definir las Matemáticas debido al gran progreso que han experimentado en los últimos siglos. Se ha venido afirmando que las Matemáticas estudian el número y la extensión, pero esta definición ha quedado anticuada. Vamos a exponer un esquema muy simplificado de las distintas partes de esta ciencia para hacernos una idea de su contenido:
En los fundamentos de las Matemáticas, está la teoría de los conjuntos y la Lógica.
Esta fundamentación ha dado origen a la matemática moderna que ha supuesto una revolución. Esta revolución surgió para dar al conjunto de los conocimientos matemáticos una mayor consistencia y coherencia. Tal fue la intención de sus creadores, Hilbert, Cantor y Russell. También fueron importantes las aportaciones de los matemáticos franceses reunidos bajo el nombre de Nicolás Bourbaki. Para todos ellos era más importante enunciar y demostrar con el máximo rigor los principales teoremas de las Matemáticas que descubrir otros nuevos.
Este nuevo enfoque de las Matemáticas, concibe a esta ciencia como un sistema formal axiomático. Si conseguimos entender estas palabras, habremos comprendido la estructura de las Matemáticas.
Un sistema formal axiomático, está constituido por un conjunto de proposiciones llamadas tesis del sistema, de las que unas son los axiomas y otras los teoremas.
Los axiomas
Son las proposiciones básicas del sistema. Axioma viene del griego αξιωματα que significa dignidades. Son las proposiciones más dignas, las primeras. Así las bautizó Euclides en sus Elementos. Antiguamente estos axiomas eran evidentes; es decir, su verdad se imponía inmediatamente a la mente. Son los llamados axiomas materiales.
En la actualidad, sin embargo, los axiomas se enuncian como axiomas formales, como proposiciones cuya verdad no se plantea como problema, pero que se establecen como fundamento de todas las demás proposiciones del sistema formal axiomático.
Para hacernos una idea adecuada del sistema formal axiomático, pondremos como ejemplo, el del juego de ajedrez. Los axiomas son las reglas del juego, de las que no se pueden salir los jugadores, y, por tanto, en los sistemas formales axiomáticos, los axiomas deben quedar bien establecidos para que se puedan deducir los teoremas con ausencia de contradicción.
Los teoremas
Son las proposiciones o tesis del sistema formal axiomático que se demuestran a partir de los axiomas, o a partir de otros teoremas ya demostrados.
Estructura de un sistema formal axiomático
- Parte morfológica
- Un conjunto de componentes primitivos.
- Un conjunto de operaciones relativas a tales componentes.
- Un conjunto de reglas de formación expresivas de cómo a partir de los componentes primitivos se pueden construir nuevos componentes llamados derivados.
- Parte axiomática
- Un conjunto de axiomas.
- Un conjunto de definiciones.
- Un conjunto de reglas o criterios de deducción.
- Un conjunto de teoremas demostrados, que se basan en los tres conjuntos anteriores.
Lo que se refiere a la parte morfológica, lo hemos estudiado en la Lógica proposicional. En cuanto a la parte axiomática, se han formulado diferentes grupos de axiomas como los de Lukasiewicz, los de Frege – Lukasiewicz, y los de Hilbert – Ackermann, que pasamos a exponer.
Axiomas
- A 1:
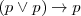
- A 2:
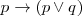
- A 3:

- A 4:
![(p \to q) \to [(r \lor p) \to (r \lor q)] (p \to q) \to [(r \lor p) \to (r \lor q)]](/images/math/math-2fb5a3e73dc79b19d27895f072d3230d.png)
Definiciones
Tienen como fin establecer el significado de los operadores no primitivos o derivados.
- Df, 1:
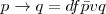
- Df, 2:
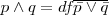
- Df. 3:
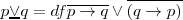
- Df. 4:
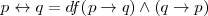
Criterios de deducción
- D 1: A 1, A 2, A 3, A 4 son tesis.
- D 2: Si
 es una tesis y si
es una tesis y si 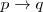 es una tesis, entonces
es una tesis, entonces 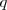 es una tesis (modus ponendo ponens).
es una tesis (modus ponendo ponens).
- D 3: Si una expresión lógica es una tesis y sustituimos en ella una proposición atómica por otra cualquiera, el resultado es una tesis.
- D 4: Si
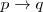 es una tesis, y si
es una tesis, y si 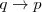 es una tesis, entonces
es una tesis, entonces 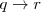 es una tesis.
es una tesis.
- D 5: Nada es tesis si no es mediante los criterios: D 1, D 2, D 3 y D 4.
A partir de estos axiomas, definiciones y criterios de deducción se pueden ir demostrando los teoremas de la lógica proposicional. Por ejemplo:
- A partir de A 2, D 1, D 3, se obtiene:
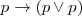 T1.
T1.
- A partir de A 1, T 1, D 1, D 4:
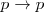 T2.
T2.
- A partir de T 2, Df 1:
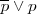 T3.
T3.
- A partir de A 3, D 1, D 3 :
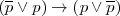 T4.
T4.
- A partir de T 3, T 4, D 2 :
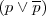 T5.
T5.
En el método matemático no existe un modelo único de sistema formal axiomático para toda la matemática. Cada una de sus partes, –según el organigrama anterior–, tiene su sistema formal axiomático.
La teoría de los conjuntos utiliza los axiomas de Zermelo – Faenkel, o los de Neumann – Bernays – Gödel. La aritmética usa los de Peano, La geometría euclídea los de Hilbert, etc.
Finalmente, para que un conjunto de axiomas esté bien construido tiene que cumplir los siguientes requisitos:
- Independencia: Ninguno de los axiomas puede ser deducido o demostrado a partir de los demás. Cada axioma ha de ser independiente.
- Consistencia: Partiendo de los axiomas no debe ser posible demostrar un teorema y la negación del mismo. No se puede demostrar que 3 + 2 sea igual a 5, y que 3 + 2 sea distinto de 5.
- Completitud: Significa que sobre cualquier proposición del sistema se pueda determinar si es verdadera o es falsa.
Al aplicar estas condiciones necesarias, surgen las limitaciones de los sistemas formales axiomáticos, que fueron descubiertas por el insigne lógico – matemático Kurt Gödel en 1931. Gödel afirma que en todo sistema formal axiomático, hay proposiciones indecidibles desde el interior del sistema, es decir, que no se puede afirmar si son verdaderas o falsas, dentro de los límites del sistema. (Habría que salirse del sistema y enunciar otros axiomas, pero esto nos llevaría a un proceso indefinido).
Algunos matemáticos consideraron dentro de este tipo de proposiciones algunas que aún no habían sido demostradas como la conjetura de Goldbach.
Finalmente, podemos preguntarnos, sobre el tipo de conocimiento y la seguridad o certeza que nos proporcionan las matemáticas, ¿son seguras sus conclusiones?
La autonomía del sistema formal axiomático es la raíz de la seguridad de sus conclusiones. Dados los axiomas, los teoremas se van deduciendo necesariamente. Volvemos a encontrar la noción de verdad lógica o validez, matemáticamente verdadero significa verdadero dentro del sistema axiomático en el que se trabaja.
Sin embargo lo interesante de las matemáticas es que también se pueden aplicar como herramienta para consolidar descubrimientos en los campos de otras ciencias como la física, la química o la astronomía.
Las matemáticas, nos ayudan a:
- Codificar y descifrar la experiencia. Por ejemplo si “Juana y Pepe pueden cortar el césped de su casa trabajando juntos en 4 horas. Si trabajara Juana sola, tardaría 6 horas, ¿cuánto tardaría Pepe si trabajara solo?
Solución: Juana 6h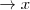
- Juana 4h
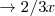
- Pepe 4h
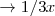 Por lo tanto, Pepe 12h
Por lo tanto, Pepe 12h 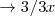
- No engañarnos con nuestros sentidos o intuiciones: Supongamos que una persona rema 2 Km, río arriba y 2Km. río abajo. Esta persona rema a 5Km. por hora en aguas tranquilas. La corriente del río es de 3 Km. por hora, ¿cuánto tiempo tardará?
Solución: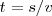
 = Tiempo
= Tiempo
 = Espacio
= Espacio
 = Velocidad
= Velocidad
Río arriba:
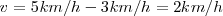
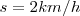
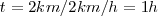
Río abajo:
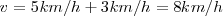
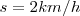
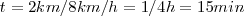
Total = 1h 15min
A esto podemos añadir que las Matemáticas también pueden apreciarse y comprenderse como un sistema separado, un lenguaje independiente, gracias al cual traducimos y organizamos nuestra experiencia para poderla entender y racionalizar. Por eso decimos que las Matemáticas son el lenguaje en el que escribimos la Física.
Los científicos de la naturaleza, físicos o astrónomos, perciben una relación entre los datos que observan y los encajan en algún patrón matemático. Kepler -el famoso astrónomo que describió el viaje de la tierra alrededor del sol en órbitas elípticas, usando los datos de Thycho Brahe sobre la órbita de Marte -, observó que los planetas se movían describiendo elipses y atribuyó estas observaciones a un error de observación, pues aún en esa época se explicaban los movimientos de los astros circularmente. Gracias a sus estudios sobre elipses y cónicas y a su admiración por las matemáticas, pudo volver a la antigua idea de la filosofía pitagórica de que la naturaleza estaba escrita en un lenguaje matemático, y enunció sus tres famosas leyes en su obra fundamental, La armonía del mundo.
En este sentido, afirma Bertrand Russell:
“Las matemáticas son, creo yo, la principal fuente de nuestra creencia en verdades eternas y exactas. Esto deja pensar que todo razonamiento exacto se aplica a objetos ideales en contraposición a los objetos sensibles…, que el pensamiento es más noble que los sentidos, y que el objeto del pensamiento es más real que los objetos de la percepción sensible”.
Todas estas reflexiones nos llevan a formularnos varias preguntas: ¿Es inventada la matemática, es decir, consiste en un conjunto de convenciones hechas y acordadas?, o, ¿es algo que el ser humano ha descubierto observando el mundo que le rodea?
Si la matemática es pura invención, ¿cómo es que funciona tan bien?, ¿cómo es que sus aplicaciones se cumplen en el mundo exterior? Si fue descubierta, ¿cómo es que parecen existir tantos sistemas axiomáticos que cumplen con el criterio de la independencia de los axiomas y que no tienen nada que ver con nuestros sentidos?
¿Cómo se originó la matemática? Podemos contestar ingenuamente que para contar cabras u ovejas, para comerciar y no ser engañados, pero cuando surgieron los números ellos mismos cautivaron la atención y el interés de los científicos. Pitágoras y su escuela mantenían la existencia de una correspondencia biyectiva entre los números y las realidades naturales, hasta que descubrieron los números irracionales como 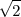 , que ya no era fácil relacionar con la experiencia, con los sentidos.
, que ya no era fácil relacionar con la experiencia, con los sentidos.
El debate sigue abierto.
El método matemático, del que venimos hablando, queda resumido en el siguiente texto:
“Euclides construyó su geometría, una geometría que resistió el paso de dos mil años, utilizando un método de trabajo especialmente acertado: el método axiomático. Euclides empezaba por enunciar una serie de verdades que le parecían evidentes por sí mismas y que aceptaba sin demostración previa. Por ejemplo que por dos puntos pasa siempre una recta, o que dos rectas no paralelas se cortan siempre en un solo punto. Una vez aceptados estos presupuestos básicos, las únicas reglas del razonamiento le proporcionaban todo lo demás. A partir de los enunciados primitivos, de los axiomas, se iban encadenando una tras otra las deducciones que se desprendían de ellos, eran los teoremas. Por supuesto, la elección de los axiomas en cierto sentido arbitraria, puede partirse de un cierto conjunto de enunciados o de otro conjunto distinto. Lo que en verdad importa es que se respeten las reglas deductivas y se mantenga el entramado total en toda su complejidad.
El método de trabajo de la matemática moderna es semejante al de Euclides, sólo que más perfecto y acabado. Supongamos que queremos edificar una teoría matemática, por ejemplo la teoría de conjuntos. Empezaremos por definir una serie de axiomas que nos aclaren lo que entendemos por los conjuntos, luego nos pondremos a deducir de acuerdo con las reglas del juego, y ésta será nuestra teoría de conjuntos. Eligiendo los axiomas con cuidado no hay que temer a la antinomias; precisamente los axiomas se pensarán de tal manera que las antinomias no puedan aparecer. Ésta es la ventaja de una teoría formalizada frente a una intuitiva. Lo único que se le pide a este juego lógico es que no nos lleve a contradicciones, es decir, que no podamos probar a la vez, a partir de los axiomas un teorema y su negación.
Un sistema de axiomas es consistente cuando no es posible probar a la vez un teorema y su contrario. El sueño de Fausto de todo matemático es probar que su ciencia está libre de contradicciones, que resiste todos los asaltos, que es consistente. Y no sólo eso, su sueño incluye el que sea completa, es decir, que todo teorema que haya sido o pueda ser pensado sea susceptible de ser probado o refutado. Por desgracia este ambicioso programa, - el programa de Hilbert -, es sólo un sueño. Un sueño del que nos despertó cruelmente en 1931 Kurt Gödel… Gödel probó que se tomaba un conjunto de axiomas lo suficientemente amplio – que contenga los axiomas de la aritmética como mínimo -, no es posible probar, con las armas de deducción del sistema, que tal conjunto sea a la vez consistente y completo. Es decir, que en caso de ser completo, contendría contradicciones. Y en caso de no tener contradicciones, -es decir, en caso de ser consistente – habría siempre teoremas verdaderos que nunca podríamos demostrar.
Gödel ha demostrado en cierto modo las limitaciones de la matemática. Esta no puede probarlo todo; en particular no puede probar su propia consistencia”.
Navarro, J. “La nueva matemática, p. 47 y ss.
Tweet