Perpendicularidad
De Wikillerato
(→Mediatriz de un segmento) |
(→Cómo se dibuja la mediatriz de un segmento AB) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 15: | Línea 15: | ||
==== Cómo se dibuja la mediatriz de un segmento AB ==== | ==== Cómo se dibuja la mediatriz de un segmento AB ==== | ||
| - | Dibujamos dos | + | Dibujamos dos puntos '''P y Q''' que equidisten de los extremos '''A y B''' del segmento. Para ello trazamos dos arcos con igual radio y centros en '''A y B'''. Su intersección son los puntos '''P y Q'''. La mediatriz '''m''' es la recta '''PQ'''. |
| + | |||
| + | [[Imagen:DibujoTecnico I-1 2.gif]] | ||
=== Trazado de la recta p perpendicular a la recta r por un punto P perteneciente a r === | === Trazado de la recta p perpendicular a la recta r por un punto P perteneciente a r === | ||
Revisión actual
Tabla de contenidos |
Definición
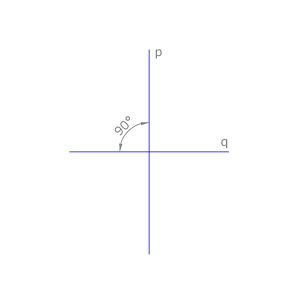
Dos rectas p y q son perpendiculares cuando se cortan formando ángulos iguales, que se llaman ángulos rectos.
Mediatriz de un segmento
La mediatriz m del segmento AB es la recta perpendicular al segmento que pasa por su punto medio.
Todo punto P perteneciente a la mediatriz equidista de los extremos A y B del segmento: PA=PB, lo que indica que el lugar geométrico de los puntos del plano que equidistan de dos puntos fijos A y B es la recta m, mediatriz del segmento AB definido por tales puntos.
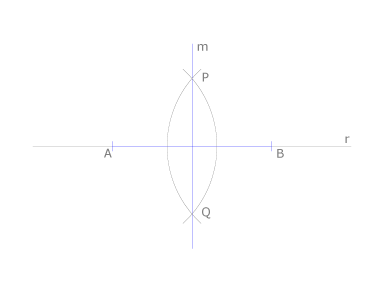
Cómo se dibuja la mediatriz de un segmento AB
Dibujamos dos puntos P y Q que equidisten de los extremos A y B del segmento. Para ello trazamos dos arcos con igual radio y centros en A y B. Su intersección son los puntos P y Q. La mediatriz m es la recta PQ.
Trazado de la recta p perpendicular a la recta r por un punto P perteneciente a r
Vamos a resolver este problema por distintos métodos:
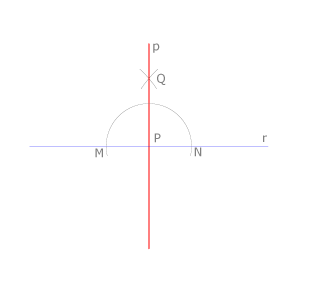
Aplicando el concepto de mediatriz
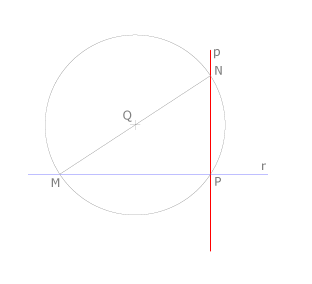
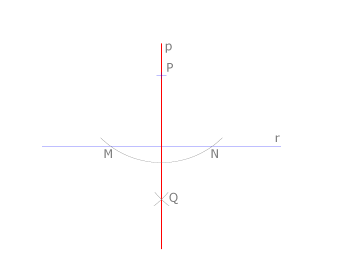
Trazamos una circunferencia de centro en P y radio arbitrario, que corta a la recta en los puntos M y N. La recta p es la mediatriz de MN.
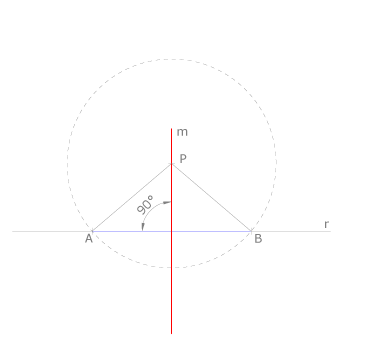
Aplicando el concepto de arco capaz
Consideramos un punto arbitrario Q y, con centro en él, trazamos una circunferencia de radio QP que corta a la recta en otro punto, M. La recta MQ corta a la circunferencia en el punto N. La recta perpendicular buscada es la definida por P y N, ya que el ángulo MPN es recto porque abarca un arco de 180º.
Aplicando el Teorema de Pitágoras
Recordamos que tres números que cumplan el teorema de Pitágoras se llaman pitagóricos. La terna de números pitagóricos más sencilla es 3,4 5, ya que
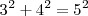
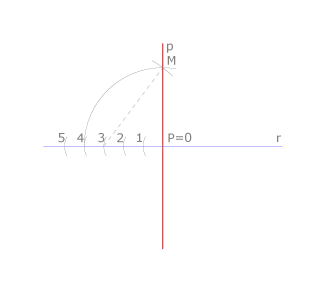
A partir del punto P=0 trazamos un arco de radio arbitrario 01 al que consideramos la unidad. Así trazamos cinco unidades que numeramos 1, 2, 3, 4, 5. Con centro en P dibujamos un arco de radio P4, con centro en 3 trazamos un arco de radio igual a cinco unidades. Los arcos se cortarán en el punto M. La recta PM es la perpendicular buscada, ya que el triángulo de vértices 3PM es rectángulo, pues sus lados miden 3, 4 y 5 unidades.
Construcción particular para trazar una perpendicular por el extremo de un segmento o de una semirrecta
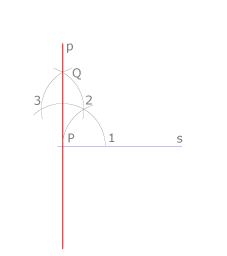
Esta construcción es una variante de la nº 1, en la que aplicábamos el concepto de mediatriz. Trazamos un arco de radio arbitrario con centro en P. Este arco corta a la recta en el punto 1. Con centro en 1 y con el mismo radio obtenemos el punto 2 sobre el arco anterior y con centro en 2, siempre con el mismo radio, obtenemos 3 sobre el mismo arco. Con centro en 3 y con el mismo radio obtenemos el punto Q.
PQ es la recta buscada. Comprobamos que PQ es la mediatriz del segmento de extremos 2 y 3.
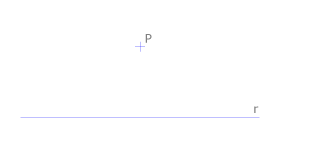
Trazado de la recta p perpendicular a la recta r por un punto P que no pertenece a r
Esta construcción es una aplicación del concepto de mediatriz. Se traza un arco de radio arbitrario y centro en P que corte a la recta r en dos puntos M y N. La mediatriz de MN es la recta p buscada.
Tweet