Reducción de las razones trigonometricas
De Wikillerato
| Línea 88: | Línea 88: | ||
<br/> | <br/> | ||
| + | |||
| + | Otra manera de obtener las relaciones que muestran la tabla es representando ambos | ||
| + | angulos en la circunferencia goniometrica. Por ejemplo, si representamos en la | ||
| + | circunferencia goniometrica | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | 180^\circ \, - \, \alpha | ||
| + | </math>: | ||
| + | |||
| + | <center> | ||
| + | [[Imagen:circulo2.png]] | ||
| + | </center> | ||
| + | |||
| + | se observa facilmente que el coseno de | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | , la abcisa ( x ) del punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | coincide con el opuesto del coseno de | ||
| + | se observa facilmente que el coseno de | ||
| + | <math> | ||
| + | 180^\circ \, - \, \alpha | ||
| + | </math> | ||
| + | , la abcisa del punto | ||
| + | <math> | ||
| + | P^\prime | ||
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
==Ejemplo== | ==Ejemplo== | ||
Revisión de 12:32 10 ene 2007
En este apartado veremos que las razones trigonométricas de cualquier angulo son
calculables a partir de las de ángulos comprendidos entre
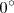 y
y 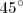 .
.
Para ello utilizaremos la siguiente tabla:
Por ejemplo, para conocer cual es la relación entre el coseno de
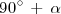 y las razones trigonometricas de
y las razones trigonometricas de
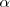 , mirariamos a la celda situada en la quinta columna y segunda fila, para encontrar que:
, mirariamos a la celda situada en la quinta columna y segunda fila, para encontrar que:
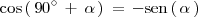
Las relaciones que muestran la tabla se pueden obtener a partir de la formulas del coseno y del seno de la suma y de la diferencia de dos angulos. Por ejemplo:
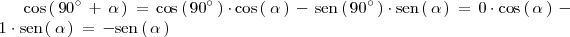
Otra manera de obtener las relaciones que muestran la tabla es representando ambos
angulos en la circunferencia goniometrica. Por ejemplo, si representamos en la
circunferencia goniometrica
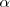 y
y
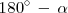 :
:
se observa facilmente que el coseno de
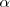 , la abcisa ( x ) del punto
, la abcisa ( x ) del punto
 coincide con el opuesto del coseno de
se observa facilmente que el coseno de
coincide con el opuesto del coseno de
se observa facilmente que el coseno de
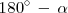 , la abcisa del punto
, la abcisa del punto
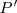 :
:
Ejemplo
Veamos un ejemplo de como se puede utilizar la tabla de arriba para calcular la tangente de
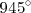 :
:
Si dividimos
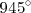 entre
entre
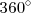 obtenemos como cociente
obtenemos como cociente
 y como resto
y como resto
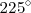 . Es decir:
. Es decir:
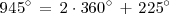
Utilizando la segunda columna de la tabla anterior, con
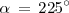 y
y
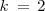 , tenemos que:
, tenemos que:
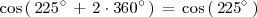
y
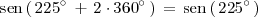
Así
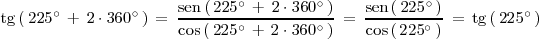
Por otra parte
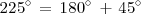
A partir de la cuarta fila de la tabla deducimos que:
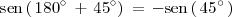
y
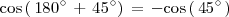
Por lo tanto,
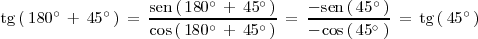
con lo cual