Trazados generales y particulares
De Wikillerato
(→Cuando el dato es el radio) |
(→Método general) |
||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
Vamos a ver dos: la construcción general a partir del '''radio''' y la construcción general a partir del '''lado.''' | Vamos a ver dos: la construcción general a partir del '''radio''' y la construcción general a partir del '''lado.''' | ||
| - | ==== | + | ====Método general==== |
| - | Se dibuja en primer lugar la circunferencia correspondiente. El problema se basa en dividir dicha circunferencia en tantas partes iguales como lados tenga el polígono que queremos trazar. | + | Se dibuja en primer lugar la circunferencia correspondiente. El problema se basa en dividir dicha circunferencia en tantas partes iguales como lados tenga el polígono que queremos trazar. Esta es una solución gráfica que no tiene solución general exacta. |
Dividimos un diámetro de la circunferencia en tantas partes iguales como lados tenga el polígono, aplicando el teorema de Tales. | Dividimos un diámetro de la circunferencia en tantas partes iguales como lados tenga el polígono, aplicando el teorema de Tales. | ||
| Línea 18: | Línea 18: | ||
Numeramos de 0 a n. En nuestro ejemplo '''n=9''', porque vamos a trazar un '''eneágono. ''' | Numeramos de 0 a n. En nuestro ejemplo '''n=9''', porque vamos a trazar un '''eneágono. ''' | ||
| - | Trazamos dos arcos con centro en '''0''' y en '''9''' y radio el '''diámetro'''. Estos arcos se cortan en los puntos '''P''' y '''Q'''. | + | Trazamos dos arcos con centro en '''0''' y en '''9''' y radio el '''diámetro'''. Estos arcos se cortan en los puntos '''P''' y '''Q'''. |
| + | |||
| + | Unimos con una recta P y/o Q con el centro de la circunferencia. (Al pasar por 0 sirve de guía y resulta más exacto cuando los alumnos lo dibujan) | ||
El segmento '''P2''' corta a la circunferencia en el punto '''B'''. El arco '''0B''' es la novena parte de la circunferencia, aproximadamente. | El segmento '''P2''' corta a la circunferencia en el punto '''B'''. El arco '''0B''' es la novena parte de la circunferencia, aproximadamente. | ||
| Línea 88: | Línea 90: | ||
[[Imagen:DibujoTecnico I-4 13.gif]] | [[Imagen:DibujoTecnico I-4 13.gif]] | ||
| - | Cuando '''el dato es el radio''': Dibujamos la circunferencia circunscrita, hallamos la mediatriz de un diámetro y la de uno de los radios que contiene. Con centro en '''P''' y radio '''PA''' trazamos un arco que corta al diámetro en '''Q'''. El segmento '''PQ''' es el | + | Cuando '''el dato es el radio''': Dibujamos la circunferencia circunscrita, hallamos la mediatriz de un diámetro y la de uno de los radios que contiene. Con centro en '''P''' y radio '''PA''' trazamos un arco que corta al diámetro en '''Q'''. El segmento '''PQ''' es el lado del pentágono inscrito. |
[[Imagen:DibujoTecnico I-4 11.gif]] | [[Imagen:DibujoTecnico I-4 11.gif]] | ||
Revisión actual
Los trazados generales de los polígonos regulares nos sirven para dibujar cualquier polígono, teniendo como dato el lado o el radio. Estas construcciones no son exactas.
Los trazados particulares nos sirven para dibujar sólo un tipo de polígonos regulares, a partir del lado o del radio. Estas construcciones son exactas en su mayoría.
Tabla de contenidos |
Trazados generales
Vamos a ver dos: la construcción general a partir del radio y la construcción general a partir del lado.
Método general
Se dibuja en primer lugar la circunferencia correspondiente. El problema se basa en dividir dicha circunferencia en tantas partes iguales como lados tenga el polígono que queremos trazar. Esta es una solución gráfica que no tiene solución general exacta.
Dividimos un diámetro de la circunferencia en tantas partes iguales como lados tenga el polígono, aplicando el teorema de Tales.
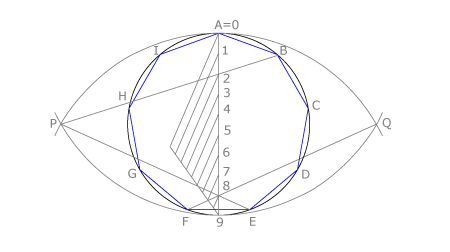
Numeramos de 0 a n. En nuestro ejemplo n=9, porque vamos a trazar un eneágono.
Trazamos dos arcos con centro en 0 y en 9 y radio el diámetro. Estos arcos se cortan en los puntos P y Q.
Unimos con una recta P y/o Q con el centro de la circunferencia. (Al pasar por 0 sirve de guía y resulta más exacto cuando los alumnos lo dibujan)
El segmento P2 corta a la circunferencia en el punto B. El arco 0B es la novena parte de la circunferencia, aproximadamente.
Obtenemos la misma medida si dibujamos el arco EF, trazando los segmentos P8 y Q8.
Trasladamos la magnitud del arco y dibujamos el polígono inscrito en la circunferencia de partida.
Para dibujar el polígono circunscrito a dicha circunferencia se trazan tangentes en cada uno de los puntos A, B, C... obtenidos.
Se realiza esta operación sea cual sea el valor de n.
Cuando el dato es el lado
Dibujamos el segmento AB, lado del polígono.
Dibujamos los arcos de radio AB con centros en A y en B. Trazamos la mediatriz y señalamos el punto 6. Con centro en 6 trazamos el arco AB de igual radio, que corta a la mediatriz en el punto 0. Dividimos 06 en seis partes iguales.
Si el polígono tiene 9 lados llevamos sobre la mediatriz, a partir del punto 6 tres unidades de las obtenidas al dividir AB y señalamos el punto 9. Con centro en 9 y radio 9A trazamos la circunferencia circunscrita al eneágono de lado AB.
Dibujamos el polígono.
Si queremos dibujar un polígono de n lados seguimos los mismos pasos y colocamos sobre la mediatriz unidades hasta alcanzar n, número de lados deseado. Así obtenemos el centro de la circunferencia circunscrita correspondiente, de radio nA.
Trazados particulares
Cuando el dato es el radio
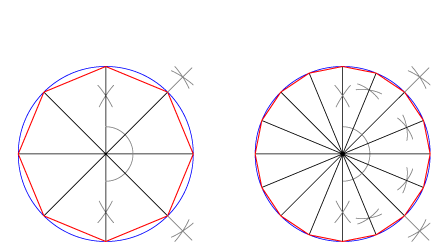
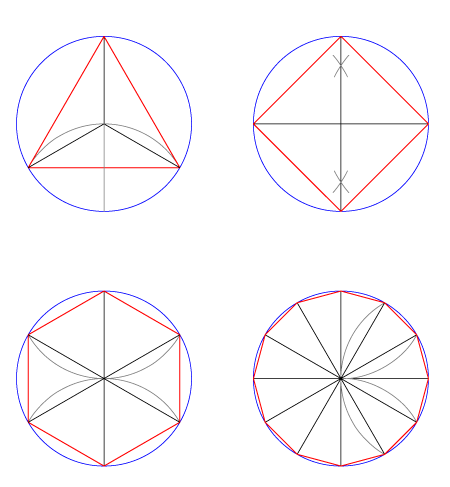
Existen varias construcciones exactas coincidentes con las posibilidades gráficas de dividir un ángulo completo en partes iguales.
Podemos dibujar así: el triángulo equilátero (360º/3), el cuadrado (360º/4), el hexágono (360º/6), el dodecágono (360º/12) o el octógono (360º/8).
Si trazamos bisectrices de los ángulos obtenidos en cada caso hallaremos polígonos con el doble de lados.
para trazos para el exagono debes hacer un circulo luego dividir en dos con una recta vertivcal y haciendo dos medias circuferencias trazando a los puntos opuestos
El heptágono regular de radio r
Existe una construcción aproximada del heptágono regular basada en que el lado del heptágono inscrito es aproximadamente igual a la altura del triángulo equilátero cuyo lado es el radio r.
Cuando el dato es el lado
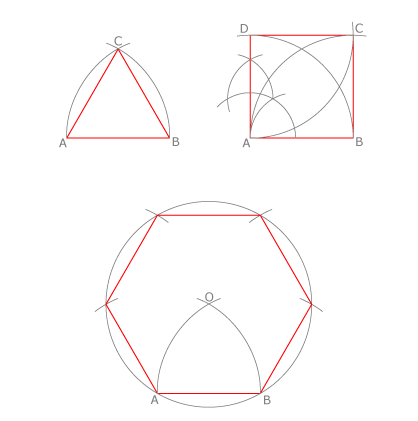
Recordamos las construcciones del triángulo equilátero, el cuadrado y el hexágono regular a partir del lado.
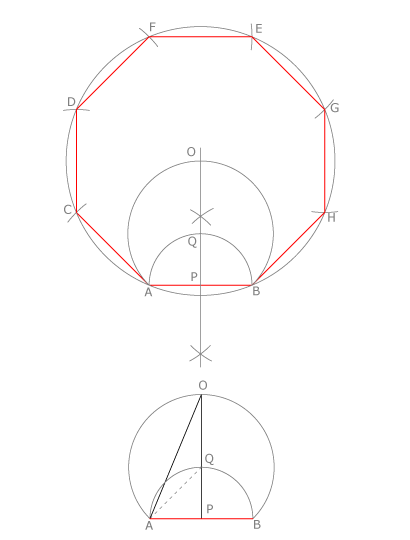
El octógono regular se dibuja trazando la mediatriz de su lado y construyendo 45º por un extremo A del mismo. Se obtiene así el centro Q de la circunscrita al cuadrado de igual lado. La circunferencia de radio QA corta a la mediatriz en el centro O del octógono.
El pentágono regular
Las construcciones exactas del pentágono regular se deben a Hipócrates y se basan en la proporción áurea pues la razón entre la diagonal y el lado del pentágono es igual a Ф: d/l=Ф.
Vamos a ver cómo se realizan las construcciones y en el próximo capítulo, dedicado a la proporcionalidad directa, veremos las demostraciones correspondientes.
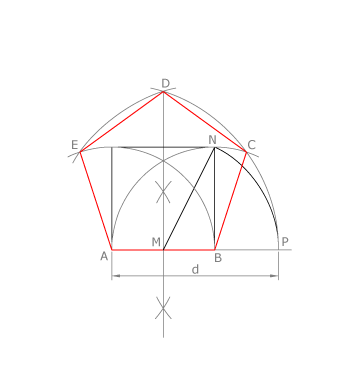
Cuando el dato es el lado AB: dibujamos el cuadrado de lado AB y la mediatriz de dicho lado. Con centro en N y radio NM trazamos un arco que corta a la prolongación de AB en el punto P. AP es la diagonal del pentágono, pues AP/AB=Ф.
Para construir el pentágono basta con realizar una triangulación colocando adecuadamente lados y diagonales.
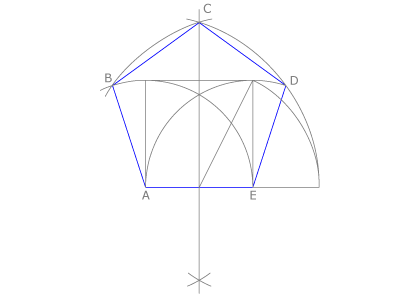
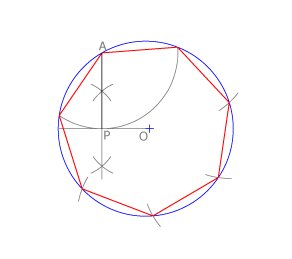
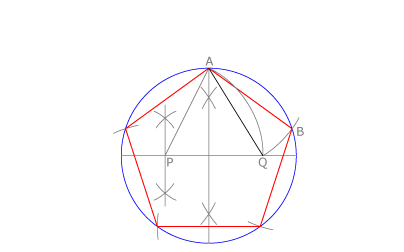
Cuando el dato es el radio: Dibujamos la circunferencia circunscrita, hallamos la mediatriz de un diámetro y la de uno de los radios que contiene. Con centro en P y radio PA trazamos un arco que corta al diámetro en Q. El segmento PQ es el lado del pentágono inscrito.
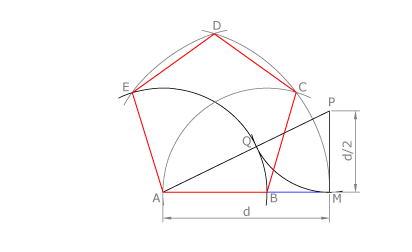
Cuando el dato es la diagonal: Utilizamos otra construcción de la segmentación áurea. Por un extremo de d trazamos un segmento perpendicular de magnitud d/2 y dibujamos el triángulo rectángulo AMP de catetos d y d/2. Con centro en P y radio PH trazamos un arco que corta a la hipotenusa en el punto Q. Con centro en A trazamos un arco de radio AQ que corta a d en el punto B.
AB es el lado del pentágono regular de diagonal d, ya que d/AB=Ф.
Otros trazados
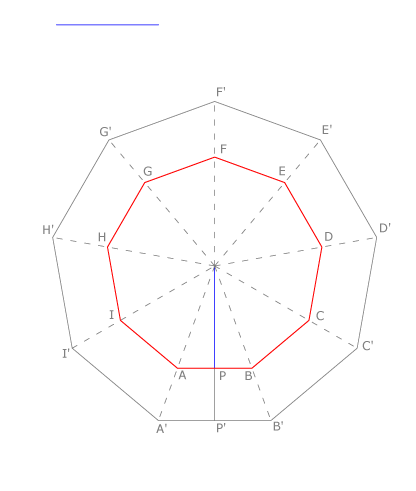
Cuando los datos son otros, como el apotema o una diagonal, suelen dibujarse los polígonos regulares aplicando una semejanza. En general, se dibuja un polígono semejante de tamaño libre y se aplica el dato.
En nuestro ejemplo dibujamos un eneágono de apotema dado. Trazamos un eneágono A’B’C’D’E’F’G’H’I’, dibujamos uno de sus apotemas y situamos sobre él el dato. Dibujamos los radios del polígono de partida y trazamos la paralela AB al lado A’B’ y las restantes paralelas a los otros lados hasta completar el polígono pedido ABCDEFGHI.
Polígonos estrellados
Si dibujamos todas las diagonales de igual tamaño de un polígono obtenemos un polígono estrellado. Si prolongamos sus lados también.
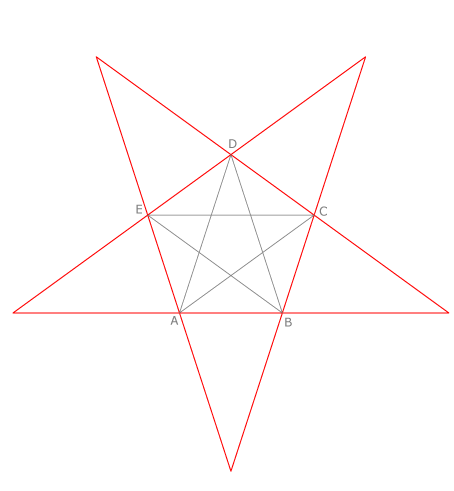
Los polígonos regulares estrellados tienen mucha aplicación en el mundo del diseño. En el ejemplo vemos un pentágono regular con el estrellado definido por sus diagonales y el obtenido prolongando sus lados.
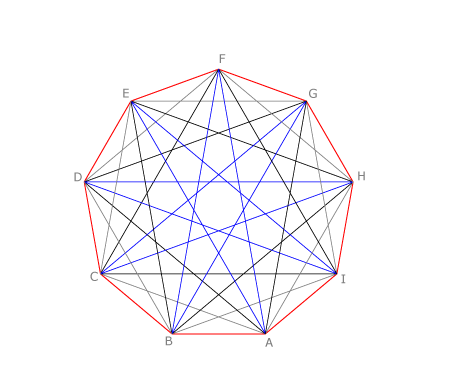
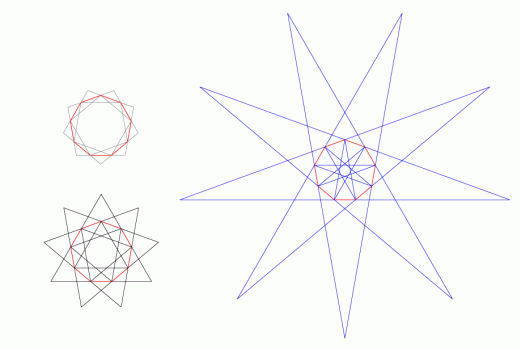
Si el polígono tiene más lados tendrá tantos estrellados inscritos como tamaños de diagonales. En el ejemplo vemos un eneágono con sus tres polígonos estrellados.
En cuanto a los obtenidos por la prolongación de los lados, podemos comprobar que son estrellados semejantes a los obtenidos con las diagonales.
Redes y teselaciones
Redes
Una red es un conjunto de polígonos iguales capaces de ensamblarse entre sí cubriendo completamente el plano.
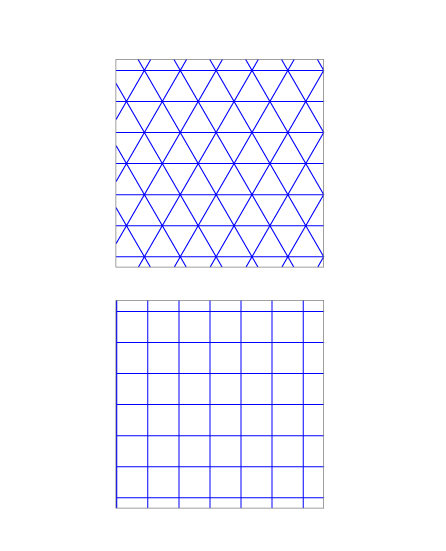
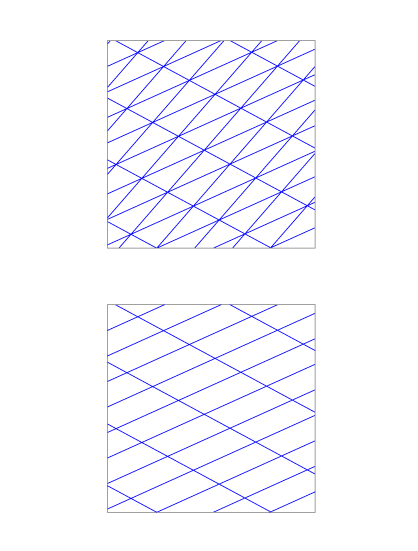
Con polígonos regulares podemos formar redes de triángulos equiláteros y de cuadrados.
La red de hexágonos puede considerarse derivada de la red de triángulos equiláteros.
Con polígonos no regulares se pueden formar redes con cualquier triángulo y con cualquier cuadrilátero.
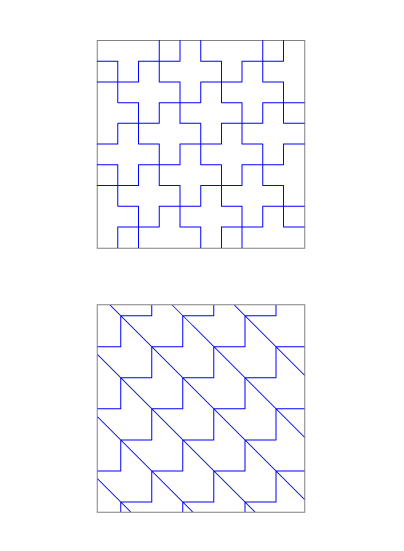
También hay muchas de redes formadas por polígonos cóncavos.
Teselaciones
Una teselación es un conjunto de polígonos de dos o más formas distintas capaces de ensamblarse entre sí cubriendo completamente el plano.
Si consideramos formas regulares, existen distintas combinaciones.
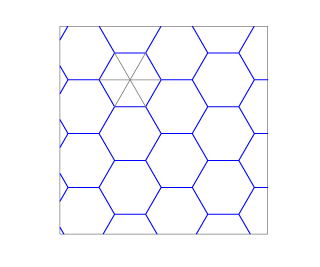
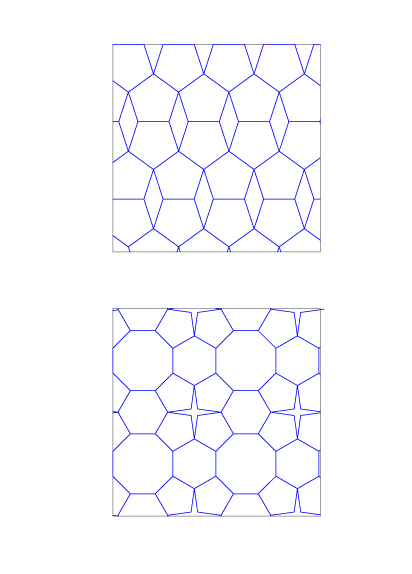
Las que vemos en el ejemplo están formadas por cuadrados, triángulos equiláteros y hexágonos.
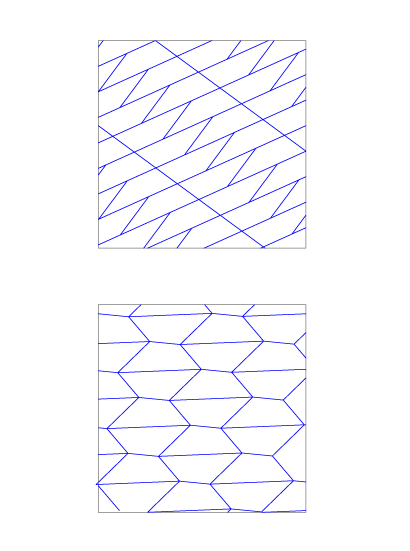
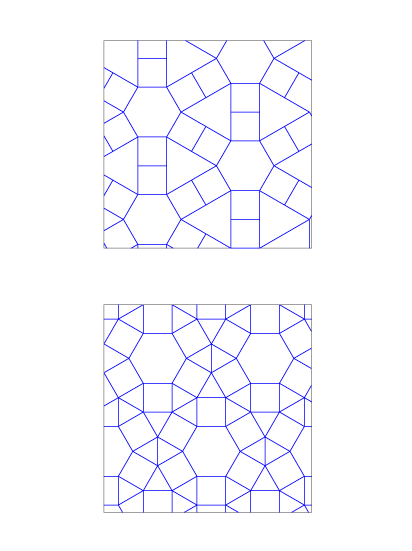
Si combinamos formas regulares con otras formas podemos conseguir teselaciones como las del siguiente ejemplo, formadas por pentágonos regulares y rombos en el primer caso y por octógonos y hexágonos regulares, pentágonos irregulares y octógonos irregulares cóncavos en el segundo.
Para comprobar que el pentágono del ejemplo es irregular basta con sumar los ángulos que confluyen en un vértice de la teselación: 120º del hexágono regular sumado a los 135º del octógono regular son 255º. Como 360º-255º= 105º el pentágono no es regular, ya que el pentágono regular tiene un ángulo de 108º.
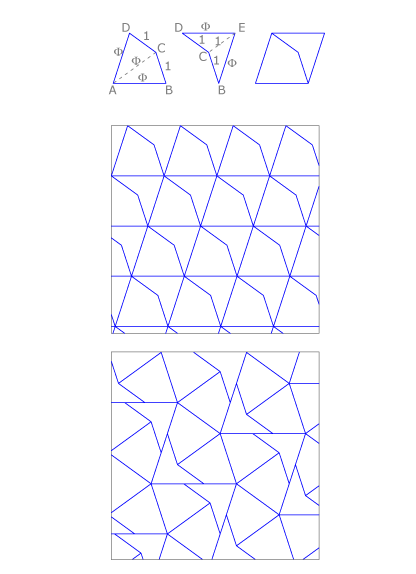
La teselación de Penrose
Es una teselación muy interesante que está formada por un cuadrilátero cóncavo y otro convexo que se ensamblan formando un rombo de lado Ф, siendo la unidad la magnitud de los otros lados, como vemos en la imagen.
Puede ensamblarse de muy distintas maneras.
Algunos problemas con polígonos regulares
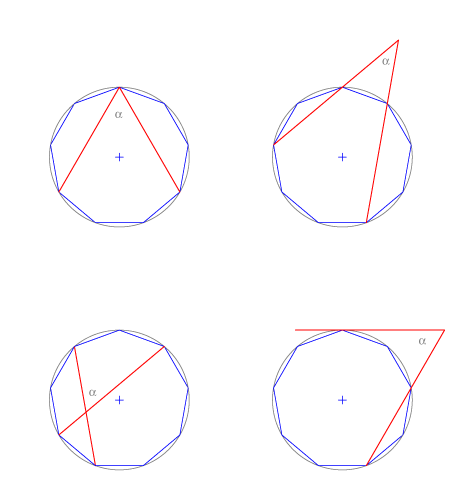
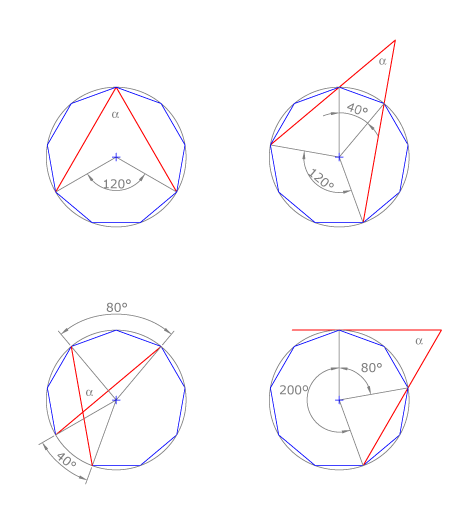
Problema I: Valor del ángulo α en cada uno de los casos expuestos.
Todos los casos están referidos a un eneágono regular inscrito. El ángulo central que abarca el arco cuya cuerda es el lado del eneágono regular vale 360º/9=40º. En el primer caso, α es un ángulo inscrito que abarca un arco que contiene tres lados del polígono y vale 40 • 3= 120º. Por lo tanto, α = 60º.
En el segundo caso, α es un ángulo exterior con los lados secantes a la circunferencia. Estos lados definen arcos de 120º y de 40º, luego el valor de α es la mitad de su diferencia: α = (120º- 40º)/2 = 40º.
En el tercer caso, α es un ángulo interior cuyos lados definen arcos de 80º y 40º, luego el valor de α es la mitad de su suma: α = (80º+40º)/2 = 60º.
En el cuarto caso, α es un ángulo exterior con un lado secante y otro tangente a la circunferencia. Estos lados definen arcos de 200º y de 80º, luego el valor de α es la mitad de su diferencia: α = (200º- 80º)/2 = 60º.
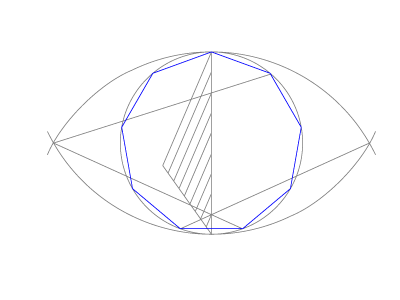
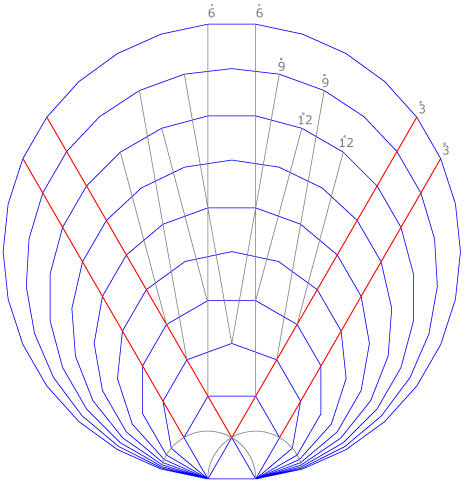
Problema II: Busca relaciones entre los polígonos de lado común AB que tengan como número de lados a los diez primeros múltiplos de tres.
Dibujamos los diez polígonos y comprobamos que todos tienen pares de lados paralelos entre sí apoyados en rectas paralelas, si su número de lados es múltiplos de tres, de seis, de nueve o de doce. Señalamos dichas rectas con el símbolo que indica múltiplo de, que es un punto sobre el número correspondiente.
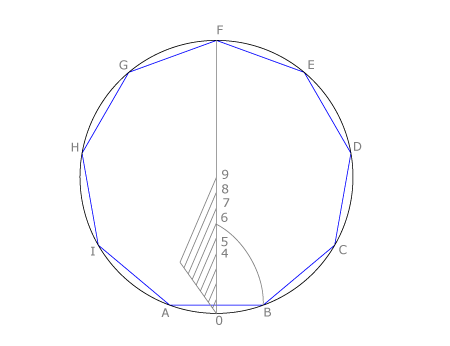
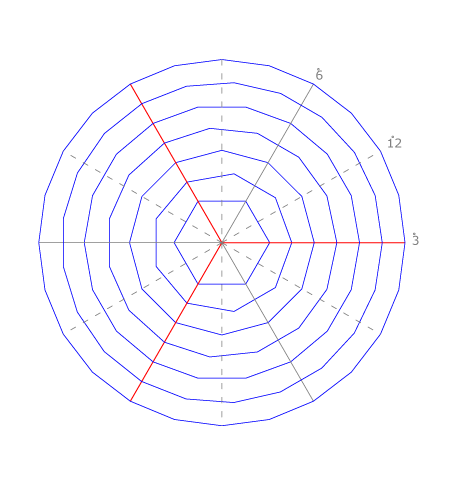
Problema III: Busca relaciones entre los polígonos concéntricos de lado dado AB que tengan como número de lados a los diez primeros múltiplos de tres.
En esta ocasión vemos que los vértices están alineados cuando los polígonos tienen número de lados múltiplo de tres, de seis y de doce.
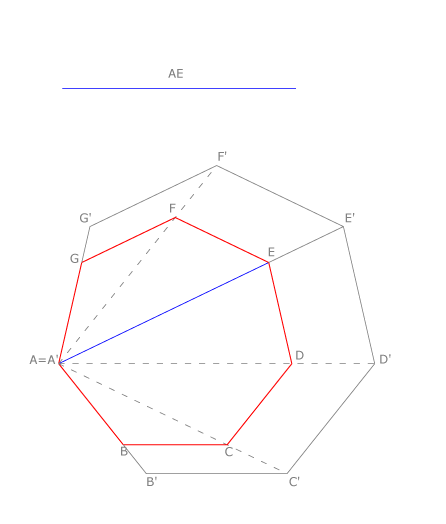
Problema IV: Heptágono regular de diagonal dada AE.
Dibujamos un heptágono regular de datos libres al que llamamos A’B’C’D’E’F’G’ y señalamos en él la diagonal A’E’. Desde el punto A’ trazamos las restantes diagonales. Superponemos a la diagonal A’E’ la diagonal AE dada, señalando el punto E.
Por E trazamos paralelas a E’F’ y a E’D’, obteniendo los lados ED y EF del heptágono solución. Trazamos ordenadamente paralelas a los restantes lados y dibujamos el polígono.
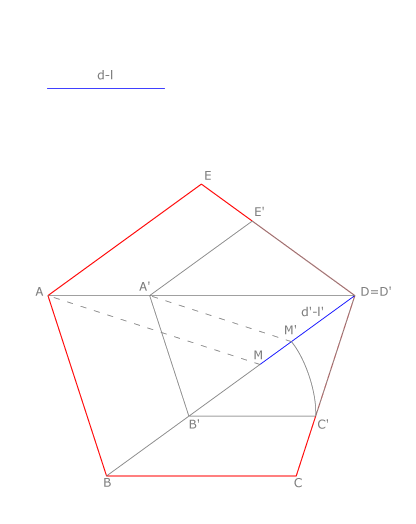
Problema V: Pentágono regular de diagonal d y lado l siendo d-l un segmento dado.
Dibujamos un pentágono A’B’C’D’E’de datos libres, dibujamos su diagonal y le restamos su lado. Obtenemos el segmento d’-l’= D’M’. Le superponemos el segmento
d-l =DM dado. Dibujamos la otra diagonal que pasa por D’, la recta A’M’ y su paralela AM. Desde A trazamos paralelas a los otros lados y construimos la solución ABCDE.
Tweet