Navegación
Discontinuidades
De Wikillerato
(Diferencias entre revisiones)
| Línea 39: | Línea 39: | ||
\mathrm{f} \left( \, x \, \right) \, = \, | \mathrm{f} \left( \, x \, \right) \, = \, | ||
\left\{ | \left\{ | ||
| - | \begin{array}[c]{ | + | \begin{array}[c]{rcl} |
| - | \frac{x^2 \, - \, 1}{x \, + \, 1}, & \qquad \makebox{si} x \neq 1 | + | \frac{x^2 \, - \, 1}{x \, + \, 1} & , & \qquad \makebox{si} x \neq 1 |
\\ | \\ | ||
| - | 0, & \qquad \makebox{si} x \, = \, 1 | + | 0 & , & \qquad \makebox{si} x \, = \, 1 |
\end{array} | \end{array} | ||
\right. | \right. | ||
Revisión de 14:11 11 ene 2007
Una función es discontinua en un punto
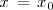si
no es continua en dicho punto.
Una función
tiene una discontinuidad evitable en un punto
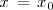cuando existe el limite de la función en dicho punto.
Ejemplo
La función
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, + \, 1} & , & \qquad \makebox{si} x \neq 1
\\
0 & , & \qquad \makebox{si} x \, = \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-0e03039bbec41714478545edd71fcc20.png "\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, + \, 1} & , & \qquad \makebox{si} x \neq 1
\\
0 & , & \qquad \makebox{si} x \, = \, 1
\end{array}
</pre>
<p>\right.")
