Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

La derivada como una tasa de variación instantánea

De Wikillerato

(Diferencias entre revisiones)
Línea 3: Línea 3:
<br/>
<br/>
-
Supongamos que un coche formula uno se mueve en una carretera totalmente recta. A
+
Supongamos que un coche de formula uno se mueve en una carretera totalmente recta. A
distintas distancias de la salida se registran los tiempos de paso, obteniendose la
distintas distancias de la salida se registran los tiempos de paso, obteniendose la
siguiente tabla:
siguiente tabla:
Línea 54: Línea 54:
<math>
<math>
\frac{\mathrm{f} \left( \, 13.4 \, \right) \, - \, \mathrm{f} \left( \, 9 \,
\frac{\mathrm{f} \left( \, 13.4 \, \right) \, - \, \mathrm{f} \left( \, 9 \,
-
\right)}{13.4 \, - \, 9} \, = \, \frac{}{4.4}
+
\right)}{6.7 \, - \, 4.5} \, = \, 2
</math>
</math>
</center>
</center>
Línea 103: Línea 103:
a
a
</math>
</math>
-
&nbsp; en la '''''tasa de variación media'''' de la función &nbsp;
+
&nbsp; en la '''''tasa de variación media''''' de la función &nbsp;
<math>
<math>
f
f
Línea 113: Línea 113:
\right]
\right]
</math>.
</math>.
-
Por tanto, la '''''tasa de variación instantánea''''' de la función &nbsp;
+
; por tanto, la '''''tasa de variación instantánea''''' de la función &nbsp;
<math>
<math>
f
f
Línea 127: Línea 127:
<center>
<center>
<math>
<math>
-
\lim_{h \to 0}\frac{\mathbf{f}\left( \, a \, + \, h \, \right) \, - \, \mathbf{f}\left( \, a \, \right)}{h}
+
\lim_{h \to 0}\frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, \mathrm{f}\left( \, a \, \right)}{h}
</math>
</math>
</center>
</center>
Línea 141: Línea 141:
x \, = \, a
x \, = \, a
</math>.
</math>.
 +
 +
<br/>
[[Category:Matemáticas]]
[[Category:Matemáticas]]

Revisión de 16:50 11 ene 2007

Tasa de variación media


Supongamos que un coche de formula uno se mueve en una carretera totalmente recta. A distintas distancias de la salida se registran los tiempos de paso, obteniendose la siguiente tabla:


Imagen:tabla7.png


En este caso, la posición,   y , se puede ver como una función,   \mathrm{f} , del tiempo,   x . Es decir:


y \, = \, \mathrm{f} \left( \, x \, \right)


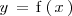
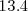La tasa de variación media de la posición en el intervalo de tiempo desde el instante   9   al instante   13.4   es:


[Unparseable or potentially dangerous latex formula. Error 3 ]


En general, la tasa de variación media de la función   \mathrm{f}   en   \left[ </p> <pre> \, a, \, b \, </pre> <p>\right]   se define como el cociente:


\frac{\mathrm{f} \left( \, b \, \right) \, - \, \mathrm{f} \left( \, a \, </p> <pre> \right)}{b \, - \, a} </pre> <p>


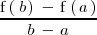
Tasa de variación instantánea


La tasa de variación instantánea de la función   f   en el punto   x \, = \, a   se obtiene haciendo tender   b   a   a   en la tasa de variación media de la función   f   en el intervalo   \left[ </p> <pre> \, a, \, b \, </pre> <p>\right] .

por tanto, la tasa de variación instantánea de la función  

f   en el punto   x \, = \, a   es


\lim_{h \to 0}\frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, \mathrm{f}\left( \, a \, \right)}{h}


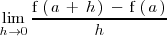
que es precisamente la derivada de la función   f   en el punto   x \, = \, a .


Obtenido de "http://wikillerato.org/La_derivada_como_una_tasa_de_variaci%C3%B3n_instant%C3%A1nea.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.