Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Función derivada de las operaciones de funciones
De Wikillerato
(Diferencias entre revisiones)
Línea 1:
Línea 1: - <math>
- \mathrm{f}
- </math>
- en el punto
- <math>
- x \, = \, a
- </math>
- ,
- <math>
- \mathrm{f}^\prime
- \left(
- \, a \,
- \right)
- </math>
- , si existe, es el valor del limite:
-
- <br/>
-
- <center>
- <math>
- \lim_{h \to 0} \frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \,
- \mathrm{f} \left( \, a \, \right)}{h}
- </math>.
- </center>
-
- <br/>
-
- Si
- <math>
- \mathrm{f}^\prime
- \left(
- \, a \,
- \right)
- </math>
- es un número real, la función
- <math>
- \mathrm{f}
- </math>
- es derivable en
- <math>
- x \, = \, a
- </math>.
- Si
- <math>
- \mathrm{f}^\prime
- \left(
- \, a \,
- \right)
- </math>
- no es un número real o el límite no existe, la función
- <math>
- \mathrm{f}
- </math>
- no es derivable en dicho punto.
-
- <br/>
-
- ==Ejemplo==
-
- <br/>
-
- Calculemos la derivada de
- <math>
- \mathrm{f}
- \left(
- \, x \,
- \right)
- \, = \, x^2
- </math>
- en
- <math>
- x \, = \, 2
- </math>:
-
- <br/>
-
- <center>
- <math>
- \mathrm{f}^\prime
- \left(
- \, 2 \,
- \right)
- \, = \, \lim_{h \to 0} \frac{\mathrm{f}\left( \, 2 \, + \, h \, \right) \, - \,
- \mathrm{f} \left( \, 2 \, \right)}{h} \, = \, \lim_{h \to 0} \frac
- {\left( \, 2 \, + \, h \, \right)^2 \, - \, 2^2}{h} \, = \,
- </math>
-
- <br/>
-
- <math>
- \, = \, \lim_{h \to 0}
- \frac {\left( \, 4 \, + \, 4h \, + \, h^2 \, \right) \, - \, 4}{h} \, = \,
- \lim_{h \to 0} \frac {4h \, + \, h^2}{h} \, = \, \lim_{h \to 0}
- \left(
- \, h \, + 4 \, \,
- \right)
- \, = \, 4
- </math>
- </center>
-
- <br/>
-
- [[Category:Matemáticas]]
- %% }}}
- %% {{{ =tasas de variación
-
- ==Tasa de variación media==
-
- <br/>
-
- Supongamos que un coche de fórmula uno se mueve en una carretera totalmente recta. A
- distintas distancias de la salida se registran los tiempos de paso, obteniendose la
- siguiente tabla:
-
- <br/>
-
- <center>
- [[Imagen:tabla7.png]]
- </center>
-
- <br/>
-
- En este caso, la posición,
- <math>
- y
- </math>
- , se puede ver como una función,
- <math>
- \mathrm{f}
- </math>
- , del tiempo,
- <math>
- x
- </math>; es decir:
-
- <br/>
-
- <center>
- <math>
- y \, = \, \mathrm{f} \left( \, x \, \right)
- </math>
- </center>
-
- <br/>
-
- La '''''tasa de variación media''''' de la posición en el intervalo de tiempo desde el
- instante
- <math>
- 9
- </math>
- al instante
- <math>
- 13.4
- </math>
- es:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f} \left( \, 13.4 \, \right) \, - \, \mathrm{f} \left( \, 9 \,
- \right)}{13.4 \, - \, 9} \, = \, \frac{6.7 \, - \, 4.5}{13.4 \, - \, 9} \, = \, 0.5
- </math>
- </center>
-
- <br/>
-
- En general, la tasa de variación media de la función
- <math>
- \mathrm{f}
- </math>
- en
- <math>
- \left[
- \, a, \, b \,
- \right]
- </math>
- se define como el cociente:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f} \left( \, b \, \right) \, - \, \mathrm{f} \left( \, a \,
- \right)}{b \, - \, a}
- </math>
- </center>
-
- <br/>
-
- ==Tasa de variación instantánea==
-
- <br/>
-
- La '''''tasa de variación instantánea''''' de la función
- <math>
- f
- </math>
- en el punto
- <math>
- x \, = \, a
- </math>
- se obtiene haciendo tender
- <math>
- b
- </math>
- a
- <math>
- a
- </math>
- en la '''''tasa de variación media''''' de la función
- <math>
- f
- </math>
- en el intervalo
- <math>
- \left[
- \, a, \, b \,
- \right]
- </math>; por tanto, la '''''tasa de variación instantánea''''' de la función
- <math>
- f
- </math>
- en el punto
- <math>
- x \, = \, a
- </math>
- es
-
- <br/>
-
- <center>
- <math>
- \lim_{h \to 0}\frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, \mathrm{f}\left( \, a \, \right)}{h}
- </math>
- </center>
-
- <br/>
-
- que es precisamente la [[Definición de derivada|derivada]] de la función
- <math>
- f
- </math>
- en el punto
- <math>
- x \, = \, a
- </math>.
-
- <br/>
-
- NOTA: En el límite anterior
- <math>
- b \, = \, a \, + \, h
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =Derivadas de las funciones elementales
-
- <center>
- [[Imagen:tablaDeDerivadas.png]]
- </center>
-
- %% }}}
- %% {{{ =función derivada
-
- Si
- <math>
- \mathrm{f}
- </math>
- es una función derivable en el intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- \subset R
- </math>
- , la '''''función derivada''''' de
- <math>
- \mathrm{f}
- </math>
- es la que a cada
- <math>
- x \in
- \left(
- \, a, \, b \,
- \right)
- </math>
- le hace corresponder la [[Definición de derivada|derivada]] de
- <math>
- \mathrm{f}
- </math>
- en dicho punto. Esta función se designa por
- <math>
- \mathrm{f}^\prime \left( \, x \, \right)
- </math>.
-
- <br/>
-
- Una función
- <math>
- \mathrm{f}
- </math>
- es '''''derivable''''' en el intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- </math>
- si lo es en cada punto del intervalo.
-
- <br/>
-
- Llamamos '''''derivada de segundo orden''''' de
- <math>
- \mathrm{f}
- </math>
- a la función derivada de
- <math>
- \mathrm{f}^\prime
- </math>.
- Esta función se denota por
- <math>
- \mathrm{f}^{\prime \prime}
- </math>.
-
- <br/>
-
- <math>
- \mathrm{f}^{\prime \prime \prime}
- </math>
- es la '''''derivada tercera''''' de
- <math>
- \mathrm{f}
- </math>
- y, en general,
- <math>
- \mathrm{f}^{\left( \, n \, \right)}
- </math>
- es la '''''derivada n-ésima''''' de
- <math>
- \mathrm{f} \left( \, x \, \right)
- </math>:
- <math>
- \mathrm{f}^{\left( \, n \, \right)}
- </math>
- es la función derivada de
- <math>
- \mathrm{f}^{\left( \, n \, - \, 1 \, \right)}
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =significado geométrico de la derivada
-
- Consideremos la grafica de una función
- <math>
- \mathrm{f}
- </math>
- . Tomemos un punto
- <math>
- A \, = \,
- \left(
- \, A_x, \, \mathrm{f} \left( \, A_x \, \right) \,
- \right)
- </math>
- en dicha grafica y consideremos una sucesión de puntos
- <math>
- A_1, \, A_2, \, A_3, \, \ldots
- </math>
- en la grafica de
- <math>
- \mathrm{f}
- </math>
- . Supongamos que todos estos puntos estan a la derecha de
- <math>
- A
- </math>
- y que cuando
- <math>
- n \to \infty
- </math>
- ,
- <math>
- A_n \to A
- </math>.
-
- <br/>
-
- La recta que pasa por los puntos
- <math>
- A
- </math>
- y
- <math>
- A_n
- </math>
- es una secante a la grafica de la función
- <math>
- \mathrm{f}
- </math>. De esta forma, hay una secante para cada punto
- <math>
- A_n
- </math>. Sea
- <math>
- s_n
- </math>
- la recta que pasa por
- <math>
- A
- </math>
- y por
- <math>
- A_n
- </math>
- .
-
- <br/>
-
- <center>
- [[Imagen:tangente.png]]
- </center>
-
- <br/>
-
- Cuando
- <math>
- n
- </math>
- tiende a
- <math>
- \infty
- </math>
- ,
- <math>
- s_n
- </math>
- tiende a la tangente a la grafica de la función
- <math>
- \mathrm{f}
- </math>
- en el punto
- <math>
- A
- </math>,
- <math>
- t
- </math>:
-
- <br/>
-
- <center>
- <math>
- s_n \to t
- </math>
- </center>
-
- <br/>
-
- Habria de esperar, pues, que la pendiente de
- <math>
- s_n
- </math>
- tienda a la pendiente de
- <math>
- t
- </math>
- cuando
- <math>
- n
- </math>
- tiende a
- <math>
- \infty
- </math>. Como la pendiente de
- <math>
- s_n
- </math>
- es una [[La derivada como una tasa de variación instantánea|tasa de variación
- media]]:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f} \left( \, A_{n,x} \, \right) \, - \, \mathrm{f} \left( \, A_x \,
- \right)}{A_{n,x} \, - \, A_x}
- </math>
-
- <br/>
-
- (<math>
- A_{n,x} \, =
- </math>
- abcisa de
- <math>
- A_n
- </math>)
- </center>
-
- <br/>
-
- su limite cuando
- <math>
- n \to \infty
- </math>
- es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de
- <math>
- \mathrm{f}
- </math>
- en
- <math>
- A_x
- </math>; es decir la pendiente de
- <math>
- t
- </math>
- es la derivada de
- <math>
- \mathrm{f}
- </math>
- en
- <math>
- A_x
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =función derivada de las operaciones de funciones
-
__TOC__
__TOC__
Revisión de 16:25 12 ene 2007
Derivada de la suma
La derivada de la suma de dos funciones es
igual a la suma de las derivadas de dichas funciones:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Este resultado, se puede ampliar a cualquier número de funciones.
Derivada de la diferencia
La derivada de la diferencia de dos funciones es
igual a la diferencia de las derivadas de dichas funciones:
[Unparseable or potentially dangerous latex formula. Error 3 ]
=Derivada del producto
La derivada del producto de dos funciones,
[Unparseable or potentially dangerous latex formula. Error 3 ]
Derivada del cociente
La derivada del cociente
[Unparseable or potentially dangerous latex formula. Error 3 ]
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
 y
y
 , viene dado por la fórmula:
, viene dado por la fórmula:
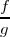 viene dado por la fórmula:
viene dado por la fórmula:



