Arco capaz
De Wikillerato
| (21 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | '''Definición''' | |
| - | + | ||
| - | + | El arco capaz es el lugar geométrico de los puntos que unidos con los extremos de un segmento forman siempre un mismo ángulo. | |
| - | + | ===Trazado del arco capaz=== | |
| - | + | Vamos a realizar dos trazados del arco capaz, del ángulo <math>\alpha</math> para un segmento <math>AB \ </math>. | |
| - | + | ||
| - | + | [[Imagen:DibujoTecnico I-1 47.gif]] | |
| + | |||
| + | Consideramos los siguientes datos: | ||
| + | |||
| + | [[Imen:DibujoT I-1 48.gif]] | ||
| + | |||
| + | '''Trazado I:''' | ||
| + | |||
| + | Dibujamos la mediatriz del segmento <math>AB \ </math>, pues el centro del arco estará sobre ella, al ser equidistante de <math>A</math> y de <math>B</math>. | ||
| + | |||
| + | Dibujamos el ángulo <math>90^\circ - \alpha</math> ,complementario del dado, con vértice en <math>A</math>. El lado de este ángulo cortará a la mediatriz en el punto <math>C</math>, centro del arco buscado. | ||
| + | |||
| + | Comprobamos que el ángulo central que abarca el arco <math>AB \ </math> mide <math> \ 2 \alpha</math>, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán <math>\alpha</math>. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 49.gif]] | ||
| + | |||
| + | '''Trazado II:''' | ||
| + | |||
| + | Dibujamos la mediatriz del segmento <math>AB \ </math>, pues el centro del arco estará sobre ella, al ser equidistante de <math>A</math> y de <math>B</math>. | ||
| + | |||
| + | Dibujamos el ángulo <math>\alpha</math> con vértice en <math>A</math>, como se ve en la figura. Trazamos por <math>A</math> la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto <math>C</math>, centro del arco buscado. | ||
| + | |||
| + | Comprobamos que el ángulo central que abarca el arco <math>AB \ </math> mide <math> \ 2 \alpha</math>, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán <math>\alpha</math>. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 50.gif]] | ||
| + | |||
| + | <h3>Enlaces externos</h3> | ||
| + | |||
| + | * [http://trazoide.com/circunferencias_y_arcos.html TRAZOIDE. Teoría y ejercicios resueltos de ARCOS en Dibujo Técnico] | ||
| + | * [http://dtaitor2.blogspot.com/2009/09/video-clases-trazados-fundamentales.html Blog de aula de Aitor Echevarría, profesor del IES Ortega y Gasset en Madrid]. Los trazados están resueltos paso a paso en formato .swf o como video clases alojadas en Youtube y embebidas en el blog. | ||
| + | |||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Definición
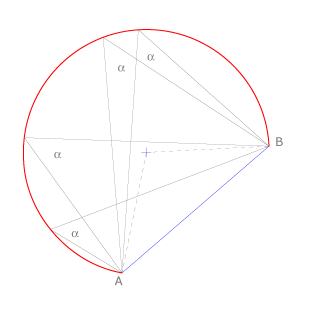
El arco capaz es el lugar geométrico de los puntos que unidos con los extremos de un segmento forman siempre un mismo ángulo.
Trazado del arco capaz
Vamos a realizar dos trazados del arco capaz, del ángulo 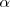 para un segmento
para un segmento 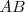 .
.
Consideramos los siguientes datos:
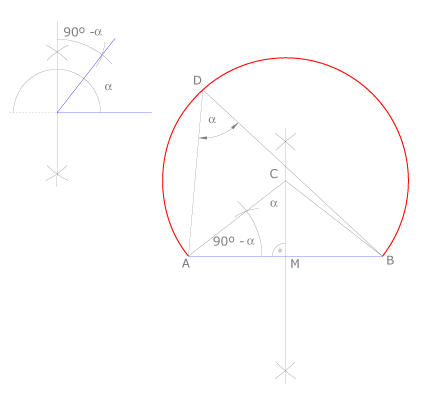
Trazado I:
Dibujamos la mediatriz del segmento 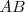 , pues el centro del arco estará sobre ella, al ser equidistante de
, pues el centro del arco estará sobre ella, al ser equidistante de  y de
y de 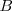 .
.
Dibujamos el ángulo 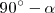 ,complementario del dado, con vértice en
,complementario del dado, con vértice en  . El lado de este ángulo cortará a la mediatriz en el punto
. El lado de este ángulo cortará a la mediatriz en el punto  , centro del arco buscado.
, centro del arco buscado.
Comprobamos que el ángulo central que abarca el arco 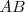 mide
mide 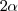 , lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán
, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán 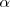 .
.
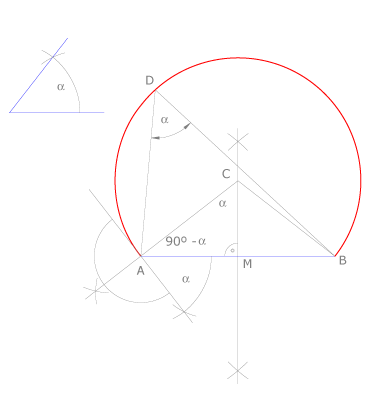
Trazado II:
Dibujamos la mediatriz del segmento 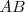 , pues el centro del arco estará sobre ella, al ser equidistante de
, pues el centro del arco estará sobre ella, al ser equidistante de  y de
y de 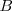 .
.
Dibujamos el ángulo 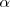 con vértice en
con vértice en  , como se ve en la figura. Trazamos por
, como se ve en la figura. Trazamos por  la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto
la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto  , centro del arco buscado.
, centro del arco buscado.
Comprobamos que el ángulo central que abarca el arco 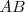 mide
mide 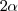 , lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán
, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán 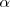 .
.
Enlaces externos
- TRAZOIDE. Teoría y ejercicios resueltos de ARCOS en Dibujo Técnico
- Blog de aula de Aitor Echevarría, profesor del IES Ortega y Gasset en Madrid. Los trazados están resueltos paso a paso en formato .swf o como video clases alojadas en Youtube y embebidas en el blog.