Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Extremos relativos
De Wikillerato
(Diferencias entre revisiones)
Línea 1:
Línea 1: - ==Función estrictamente creciente en un intervalo==
+ ==Máximo relativo ==
<br/>
<br/>
Línea 5:
Línea 5: Una función
Una función
<math>
<math>
- \mathrm{f} \left( \, x \, \right)
+ \mathrm{f}
</math>
</math>
- es '''''estrictamente creciente''''' en un intervalo
+ alcanza un '''''máximo relativo ''''' en el punto de abcisa
<math>
<math>
- \left(
+ x_0
- \, a, \, b \,
+
- \right)
+
</math>
</math>
- , si para dos valores cualesquiera del intervalo,
+ si existe un numero positivo
<math>
<math>
- x_1
+ h
</math>
</math>
- y
+ de forma que
<math>
<math>
- x_2
+ \mathrm{f} \left( \, x_0 \, \right) > \mathrm{f} \left( \, x \, \right)
</math>
</math>
- , se cumple que:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2
- \, - \, x_1} > 0
- </math>
- </center>
-
- <br/>
-
-
+ para todos los puntos
- <br/>
+
-
+
- <center>
+
- [[Imagen:funcion4.png]]
+
- </center>
+
-
+
- <br/>
+
-
+
- Cuando en la grafica de una función estrictamente creciente nos movemos hacia la derecha
+
- tambien nos movemos hacia arriba:
+
-
+
- <br/>
+
-
+
- <center>
+
<math>
<math>
- x_2 > x_1 \Rightarrow
+ x
- \mathrm{f} \left( \, x_2 \, \right) > \mathrm{f} \left( \, x_1 \, \right)
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- Una función
+
- <math>
+
- f
+
- </math>
+
- es estrictamente creciente en el punto de abcisa
+
- <math>
+
- x \, = \, a
+
- </math>
+
- si existe algun número positivo
+
- <math>
+
- h
+
- </math>
+
- tal que
+
- <math>
+
- \mathrm{f}
+
-
+
</math>
</math>
- es estrictamente creciente en el intervalo
+ del intervalo
<math>
<math>
\left(
\left(
- \, x \, - \, h, \, x \, + \, h \,
+ \, x_0 \, - \, h, \, x_0 \, + \, h \,
\right)
\right)
</math>.
</math>.
Línea 84:
Línea 33: <br/>
<br/>
- De esta esta definición se deduce que si
+ ==Mínimo relativo ==
- <math>
+
- \mathrm{f}
+
- </math>
+
- es [[Definición de derivada|derivable]] en
+
- <math>
+
- x \, = \, a
+
- </math>
+
- y
+
- <math>
+
- f
+
- </math>
+
- es estrictamente creciente en el punto de abcisa
+
- <math>
+
- x \, = \, a
+
- </math>
+
- , entonces
+
- <math>
+
- \mathrm{f}^\prime \left( \, a \, \right) \le 0
+
- </math>.
+
-
+
- <br/>
+
-
+
- ==Función creciente en un intervalo==
+
<br/>
<br/>
Línea 113:
Línea 39: Una función
Una función
<math>
<math>
- \mathrm{f} \left( \, x \, \right)
+ \mathrm{f}
</math>
</math>
- es '''''creciente''''' en un intervalo
+ alcanza un '''''mínimo relativo ''''' en el punto de abcisa
<math>
<math>
- \left(
+ x_0
- \, a, \, b \,
+
- \right)
+
</math>
</math>
- , si para dos valores cualesquiera del intervalo,
+ si existe un numero positivo
<math>
<math>
- x_1
+ h
</math>
</math>
- y
+ de forma que
<math>
<math>
- x_2
+ \mathrm{f} \left( \, x \, \right) > \mathrm{f} \left( \, x_0 \, \right)
</math>
</math>
- , se cumple que:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2
- \, - \, x_1} \ge 0
- </math>
- </center>
-
- <br/>
-
- ==Función estrictamente decreciente en un intervalo==
-
- <br/>
-
- Una función
- <math>
- \mathrm{f} \left( \, x \, \right)
- </math>
- es '''''estrictamente decreciente''''' en un intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- </math>
- , si para dos valores cualesquiera del intervalo,
- <math>
- x_1
- </math>
- y
- <math>
- x_2
- </math>
- , se cumple que:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2
- \, - \, x_1} < 0
- </math>
- </center>
-
- <br/>
-
-
+ para todos los puntos
- <br/>
+
-
+
- <center>
+
- [[Imagen:funcion5.png]]
+
- </center>
+
-
+
- <br/>
+
-
+
- Cuando en la grafica de una función estrictamente decreciente nos movemos hacia la derecha
+
- tambien nos movemos hacia abajo:
+
-
+
- <center>
+
<math>
<math>
- x_2 > x_1 \Rightarrow
+ x
- \mathrm{f} \left( \, x_2 \, \right) < \mathrm{f} \left( \, x_1 \, \right)
+
</math>
</math>
- </center>
+ del intervalo
-
+
- <br/>
+
-
+
- Una función
+
- <math>
+
- f
+
- </math>
+
- es estrictamente decreciente en el punto de abcisa
+
- <math>
+
- x \, = \, a
+
- </math>
+
- si existe algun número positivo
+
- <math>
+
- h
+
- </math>
+
- tal que
+
- <math>
+
- \mathrm{f}
+
-
+
- </math>
+
- es estrictamente decreciente en el intervalo
+
<math>
<math>
\left(
\left(
- \, x \, - \, h, \, x \, + \, h \,
+ \, x_0 \, - \, h, \, x_0 \, + \, h \,
\right)
\right)
</math>.
</math>.
-
- <br/>
-
- De esta esta definición se deduce que si
- <math>
- \mathrm{f}
- </math>
- es [[Definición de derivada|derivable]] en
- <math>
- x \, = \, a
- </math>
- y
- <math>
- f
- </math>
- es estrictamente decreciente en el punto de abcisa
- <math>
- x \, = \, a
- </math>
- , entonces
- <math>
- \mathrm{f}^\prime \left( \, a \, \right) \le 0
- </math>.
-
- <br/>
-
- ==Función decreciente en un intervalo==
-
- <br/>
-
- Una función
- <math>
- \mathrm{f} \left( \, x \, \right)
- </math>
- es '''''decreciente''''' en un intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- </math>
- , si para dos valores cualesquiera del intervalo,
- <math>
- x_1
- </math>
- y
- <math>
- x_2
- </math>
- , se cumple que:
-
- <br/>
-
- <center>
- <math>
- \frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2
- \, - \, x_1} \le 0
- </math>
- </center>
<br/>
<br/>
[[Category:Matemáticas]]
[[Category:Matemáticas]]
Revisión de 01:49 15 ene 2007
Máximo relativo
Una función
máximo relativo
Mínimo relativo
Una función
mínimo relativo
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
 alcanza un máximo relativo en el punto de abcisa
alcanza un máximo relativo en el punto de abcisa
 si existe un numero positivo
si existe un numero positivo
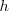 de forma que
de forma que
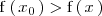 para todos los puntos
para todos los puntos
 del intervalo
del intervalo
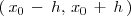 .
.
 alcanza un mínimo relativo en el punto de abcisa
alcanza un mínimo relativo en el punto de abcisa
 si existe un numero positivo
si existe un numero positivo
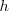 de forma que
de forma que
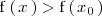 para todos los puntos
para todos los puntos
 del intervalo
del intervalo
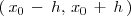 .
.



