Ley de Hooke
De Wikillerato
(Diferencias entre revisiones)
| Línea 4: | Línea 4: | ||
<flash>file=leyhooke.swf|width=390|height=195|quality=best</flash> | <flash>file=leyhooke.swf|width=390|height=195|quality=best</flash> | ||
| + | |||
| + | |||
| Línea 13: | Línea 15: | ||
Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir: | Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir: | ||
| - | <math>\vec F = - k (x - x_0) \,</math> | + | <math>\vec F = - k (\vec x - \vec x_0) \,</math> |
| + | |||
Donde <math> F</math> es la fuerza recuperadora que ejerce el resorte debido a la deformación <math>\Delta x = x - x_o </math> y <math>k</math> es la constante de elasticidad del resorte. | Donde <math> F</math> es la fuerza recuperadora que ejerce el resorte debido a la deformación <math>\Delta x = x - x_o </math> y <math>k</math> es la constante de elasticidad del resorte. | ||
| + | |||
La constante de elasticidad <math>k</math>, es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de <math>F</math>, como se ve en la ilustración, será siempre el opuesto al de la deformación <math>\Delta x</math>. | La constante de elasticidad <math>k</math>, es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de <math>F</math>, como se ve en la ilustración, será siempre el opuesto al de la deformación <math>\Delta x</math>. | ||
[[Categoría:Física|Hooke]] | [[Categoría:Física|Hooke]] | ||
Revisión de 08:53 19 sep 2007
Recordemos brevemente la Ley de Hooke, que sirve, por ejemplo, para hacer el calibrado de un dinamómetro.
Si suspendemos de un resorte una masa 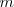 y la soltamos, ésta comienza a oscilar hasta que alcanza el equilibrio. Es decir, la masa se detiene cuando la suma de las fuerzas aplicadas sobre la masa es cero.
y la soltamos, ésta comienza a oscilar hasta que alcanza el equilibrio. Es decir, la masa se detiene cuando la suma de las fuerzas aplicadas sobre la masa es cero.
 será una fuerza de módulo igual al peso,
será una fuerza de módulo igual al peso, 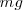 , pero tendrá sentido contrario.
, pero tendrá sentido contrario.
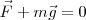 Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir:
Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir:
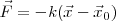 Donde
Donde 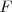 es la fuerza recuperadora que ejerce el resorte debido a la deformación
es la fuerza recuperadora que ejerce el resorte debido a la deformación 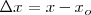 y
y 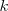 es la constante de elasticidad del resorte.
La constante de elasticidad
es la constante de elasticidad del resorte.
La constante de elasticidad 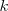 , es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de
, es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de  , como se ve en la ilustración, será siempre el opuesto al de la deformación
, como se ve en la ilustración, será siempre el opuesto al de la deformación 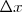 .
.



