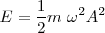Navegación
Energía e intensidad de las ondas
De Wikillerato
| Línea 7: | Línea 7: | ||
Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda | Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda | ||
| - | <math> v = \frac{dy}{dt} = \frac{d | + | <math> v = \frac{dy} {dt} = \frac{d (A \mbox { } sen ( \omega t- k x))}{dt} = \omega A \mbox { } cos ( \omega t - kz)</math> |
Dado que el valor máximo de un cos es 1, la velocidad máxima será <math>v = \omega A</math> | Dado que el valor máximo de un cos es 1, la velocidad máxima será <math>v = \omega A</math> | ||
| - | <math> E = \frac{1}{2}m \omega^2 A^2 = \frac{1}{2}m (2 \pi f)^2 A^2</math> | + | <math> E = \frac {1} {2} m \mbox { } \omega^2 A^2 = \frac{1}{2}m (2 \pi f)^2 A^2</math> |
De dónde obtenemos que la energía total que se transmite es: | De dónde obtenemos que la energía total que se transmite es: | ||
| - | <math> E = | + | <math> E = 2 \pi^2 m A^2 f^2 </math> o también |
| - | <math> E = \frac{1}{2}m \omega^2 A^2</math> | + | <math> E = \frac {1} {2} m \mbox{ } \omega ^ 2 A ^ 2 </math> |
Revisión de 12:17 7 dic 2007
Se han definido las ondas como un fenómeno de transmisión de energía sin que haya transporte de materia ¿Ahora bien, cuál es la energía que se propaga? Es evidente que la que contiene el foco emisor. Si nos atenemos a alguno de los ejemplos sencillos que se han descrito, ondas sobre una cuerda, sobre la superficie del agua, en ambos casos será la energía del oscilador, siendo la energía del oscilador igual a la energía potencial elástica que será
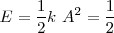
De tal modo que cuando la masa del punto M que hemos considerado en las ondas, alcanza la elongación máxima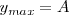 
, es decir igual a la amplitud, toda su energía será potencial, y cuando pase por las posiciones 
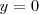toda su energía será cinética, es decir, pasará a la velocidad máxima.
Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda
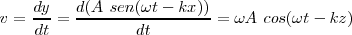
Dado que el valor máximo de un cos es 1, la velocidad máxima será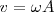 
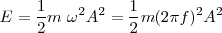
De dónde obtenemos que la energía total que se transmite es:
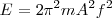o también
