Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Funciones y gráficas

De Wikillerato

(Diferencias entre revisiones)
(→Definición)
Línea 1: Línea 1:
-
==Definición==
+
y=1
-
 
+
----
-
<br/>
+
x-2
-
 
+
-
Una '''''función real de variable real''''' es toda correspondencia &nbsp;
+
-
<math>
+
-
\mathrm{f}
+
-
</math>
+
-
&nbsp; que asocia a cada elemento &nbsp;
+
-
<math>
+
-
x
+
-
</math>
+
-
&nbsp; de un subconjunto no vacio &nbsp;
+
-
<math>
+
-
D
+
-
</math>
+
-
&nbsp; de &nbsp;
+
-
<math>
+
-
R
+
-
</math>
+
-
&nbsp; un único número real. La expresamos como:
+
-
 
+
-
<br/>
+
-
 
+
-
<center>
+
-
<math>
+
-
\mathrm{f}: D \subset R \longrightarrow R
+
-
</math>
+
-
 
+
-
<br/>
+
-
 
+
-
<math>
+
-
x \longrightarrow y \, = \, \mathrm{f} \left( \, x \, \right)
+
-
</math>
+
-
</center>
+
-
 
+
-
<br/>
+
-
 
+
-
&nbsp;
+
-
<math>
+
-
x
+
-
</math>
+
-
&nbsp; es la '''''variable independiente''''' &nbsp; e &nbsp;
+
-
<math>
+
-
y
+
-
</math>
+
-
&nbsp; la '''''variable dependiente.'''''
+
-
 
+
-
<br/>
+
-
 
+
-
Al conjunto, &nbsp;
+
-
<math>
+
-
D
+
-
</math>
+
-
, de valores que toma la variable independiente &nbsp;
+
-
<math>
+
-
x
+
-
</math>
+
-
&nbsp; se le llama '''''dominio''''' de la función.
+
-
 
+
-
<br/>
+
-
 
+
-
Al conjunto de valores que toma la variable dependiente &nbsp;
+
-
<math>
+
-
y
+
-
</math>
+
-
&nbsp; se le llama '''''recorrido''''' de la función.
+
-
 
+
-
<br/>
+
-
 
+
-
Una función se define '''''explicitamente''''' si viene dada como &nbsp;
+
-
<math>
+
-
y \, = \, \mathrm{f} \left( \, x \, \right)
+
-
</math>
+
-
, es decir, si la variable dependiente, &nbsp;
+
-
<math>
+
-
y
+
-
</math>
+
-
, esta despejada.
+
-
 
+
-
<br/>
+
-
 
+
-
Una función se define '''''implícitamente''''' si viene dada en la forma &nbsp;
+
-
<math>
+
-
\mathrm{f}
+
-
\left(
+
-
\, x, \, y \,
+
-
\right)
+
-
\, = \, 0
+
-
</math>
+
-
, esto es, si la función se expone como una expresión algebraica igualada a cero.
+
-
 
+
-
<br/>
+
-
 
+
-
===Ejemplo===
+
-
 
+
-
<br/>
+
-
 
+
-
La función &nbsp;
+
-
<math>
+
-
y \, = \, \cos \left( \, x \, \right)
+
-
</math>
+
-
&nbsp; está expresada en forma explícita.
+
-
 
+
-
<br/>
+
-
 
+
-
La función &nbsp;
+
-
<math>
+
-
\log y \, - \, x \, = \, 0
+
-
</math>
+
-
&nbsp; está expresada en forma implícita.
+
-
 
+
-
<br/>
+
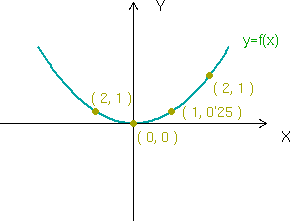
==Gráfica==
==Gráfica==

Revisión de 00:16 28 ene 2008

y=1

x-2

Gráfica


La gráfica de una función   \mathrm{f}   es el conjunto de puntos del plano definido de la siguiente forma:


\left\{ </p> <pre> \left( \, x, \, y \, \right) \in R^2 \, \left| \, y \, = \, \mathrm{f} \left( \, x \, \right) \right. </pre> <p>\right\}


Ejemplo


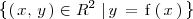
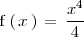La figura de abajo muestra la gráfica de la funcion   \mathrm{f} \left( \, x \, \right) \, = \, \frac{x^4}{4}   y cuatro puntos de la misma:


 


Imagen:funcion.png


Obtenido de "http://wikillerato.org/Funciones_y_gr%C3%A1ficas.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.