Concepto de velocidad
De Wikillerato
(→Velocidad instantánea) |
|||
| Línea 1: | Línea 1: | ||
| - | + | ==Velocidad media== | |
La velocidad se puede se puede definir como la variación temporal de la posición del punto material | La velocidad se puede se puede definir como la variación temporal de la posición del punto material | ||
| Línea 16: | Línea 16: | ||
<math> \vec v = \frac { \vec r (t + \Delta t) - \vec r (t)}{ \Delta t}</math> | <math> \vec v = \frac { \vec r (t + \Delta t) - \vec r (t)}{ \Delta t}</math> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==Velocidad instantánea== | ==Velocidad instantánea== | ||
| Línea 72: | Línea 66: | ||
[[Category:Física]] | [[Category:Física]] | ||
| - | |||
| - | |||
Revisión de 18:50 24 abr 2008
Tabla de contenidos |
Velocidad media
La velocidad se puede se puede definir como la variación temporal de la posición del punto material
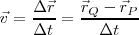
Este cociente nos define lo que llamamos velocidad media. Si consideramos que
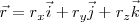
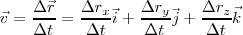
Si pretendemos calcular la velocidad entre dos instantes definidos por 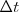 , obtenemos:
, obtenemos:
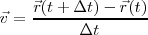
Velocidad instantánea
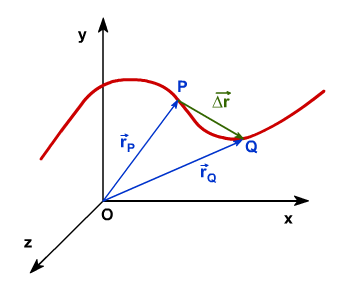
Hemos definido la velocidad media, y la hemos definido intuitivamente. Hemos trazado el vector que va desde la posición inicial a la posición final, cuya dirección siempre coincide con la cuerda que une esos dos puntos. Si hacemos cada vez más breves los intervalos de tiempo, la dirección de las cuerdas, y en consecuencia las de los vectores desplazamiento, se van aproximando a la dirección de la tangente a la trayectoria. Si pretendemos determinar la velocidad del móvil en un instante preciso, que denominaremos velocidad instantánea en el instante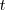 , observamos que su dirección coincidirá con la de la tangente a la trayectoria en cada instante.
, observamos que su dirección coincidirá con la de la tangente a la trayectoria en cada instante.
Y podremos calcular la velocidad en un instante t:
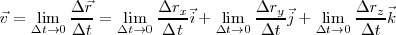
y en consecuencia:
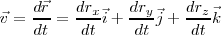
o lo que es igual :
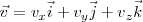
La velocidad instantánea es una magnitud vectorial cuya dirección coincide siempre con la de la tangente a la trayectoria y su sentido el del movimiento. Al módulo se le llama rapidez, que es una magnitud escalar.
En el S.I. el módulo se mide en 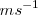 , aunque en la práctica en la Europa continental se hable más frecuentemente de
, aunque en la práctica en la Europa continental se hable más frecuentemente de 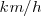 .
.
Ese módulo se obtendrá hallando la raíz cuadrada de la suma de los cuadrados de sus componentes, es decir:
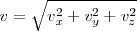
Podremos particularizar para los movimientos más estudiados en este curso, que son los movimientos sobre la recta o sobre un plano.
Movimiento sobre una recta
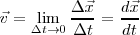
Sin embargo, dado que tanto el 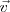 como el
como el 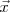 tienen la misma dirección, se podrá dar al problema un tratamiento escalar, es decir:
tienen la misma dirección, se podrá dar al problema un tratamiento escalar, es decir:
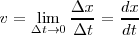
de tal modo que el sentido positivo del movimiento sobre la recta nos vendrá dado por el signo que adquiera 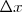 o la velocidad en la ecuación.
o la velocidad en la ecuación.
Movimiento sobre un plano
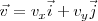
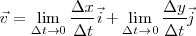
Como se verá en su momento, el moviendo sobre el plano, podrá estudiarse analizando de modo independiente las variaciones de las componentes 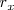 y
y 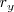 del vector posición de la partícula
del vector posición de la partícula 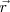 , que nos informarán acerca de las componentes
, que nos informarán acerca de las componentes 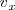 y
y 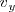 vector velocidad
vector velocidad 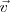 .
.
Ir a Aceleración.