|
|
| Línea 17: |
Línea 17: |
| | <math> \vec v = \frac { \vec r (t + \Delta t) - \vec r (t)}{ \Delta t}</math> | | <math> \vec v = \frac { \vec r (t + \Delta t) - \vec r (t)}{ \Delta t}</math> |
| | | | |
| - | ==Velocidad instantánea==
| + | LJKDFN V,F'''No''' ''Texto en cursiva''[[Título del enlace]][http://www.ejemplo.com Título del enlace] |
| - | | + | == Texto de titular == |
| - | Hemos definido la velocidad media, y la hemos definido intuitivamente. Hemos trazado el vector que va desde la posición inicial a la posición final, cuya dirección siempre coincide con la cuerda que une esos dos puntos. Si hacemos cada vez más breves los intervalos de tiempo, la dirección de las cuerdas, y en consecuencia las de los vectores desplazamiento, se van aproximando a la dirección de la tangente a la trayectoria. Si pretendemos determinar la velocidad del móvil en un instante preciso, que denominaremos '''velocidad instantánea en el instante'''<math> t</math>, observamos que su dirección coincidirá con la de la tangente a la trayectoria en cada instante.
| + | AA[[Imagen:Ejemplo.jpg]]AA[[Media:Ejemplo.ogg]]AA<math>Escribe aquí una fórmula</math><nowiki>Aquí inserta texto sin formato</nowiki>--[[Usuario:200.121.198.207|200.121.198.207]] 23:30 13 ago 2008 (CEST) |
| - | | + | ---- |
| - | Y podremos calcular la velocidad en un instante t:
| + | ---- |
| - |
| + | ---- |
| - | <math>\vec v= \lim_{\Delta t\to 0} \frac{\Delta \vec r }{\Delta t } = \lim_{\Delta t\to 0} \frac {\Delta r_x }{\Delta t}\vec i + \lim_{\Delta t\to 0} \frac {\Delta r_y }{\Delta t}\vec j + \lim_{\Delta t\to 0} \frac {\Delta r_z }{\Delta t}\vec k</math>
| + | ---- |
| - |
| + | ---- |
| - | y en consecuencia:
| + | ---- |
| - | | + | |
| - | <math> \vec v = \frac{ d \vec r}{ dt } = \frac{d r_x}{ dt }\vec i + \frac {d r_y}{ dt } \vec j + \frac {d r_z}{ dt }\vec k</math>
| + | |
| - | | + | |
| - | o lo que es igual :
| + | |
| - | | + | |
| - | <math> \vec v = v_x\vec i + v_y\vec j + v_z\vec k</math>
| + | |
| - | | + | |
| - | La velocidad instantánea es una magnitud vectorial cuya dirección coincide siempre con la de la tangente a la trayectoria y su sentido el del movimiento. Al módulo se le llama rapidez, que es una magnitud escalar.
| + | |
| - | | + | |
| - | En el '''S.I.''' el módulo se mide en <math>m s^{-1}</math>, aunque en la práctica en la Europa continental se hable más frecuentemente de <math>km/h</math>.
| + | |
| - | | + | |
| - | Ese módulo se obtendrá hallando la raíz cuadrada de la suma de los cuadrados de sus componentes, es decir:
| + | |
| - | | + | |
| - | <math> v = \sqrt{ v_x^2 + v_y^2 + v_z^2}</math>
| + | |
| - | | + | |
| - | Podremos particularizar para los movimientos más estudiados en este curso, que son los movimientos sobre la recta o sobre un plano.
| + | |
| - | | + | |
| - | ====Movimiento sobre una recta==== | + | |
| - | | + | |
| - | <math>\vec v = \lim_{\Delta t\to 0} \frac{\Delta\vec x}{\Delta t} =\frac{d\vec x}{dt}</math> | + | |
| - | | + | |
| - | Sin embargo, dado que tanto el <math>\vec v </math> como el <math>\vec x </math> tienen la misma dirección, se podrá dar al problema un tratamiento escalar, es decir:
| + | |
| - | | + | |
| - | <math> v = \lim_{\Delta t\to 0} \frac{\Delta x}{\Delta t} =\frac{dx}{dt}</math>
| + | |
| - |
| + | |
| - | de tal modo que el sentido positivo del movimiento sobre la recta nos vendrá dado por el signo que adquiera <math>\Delta x</math> o la velocidad en la ecuación.
| + | |
| - | | + | |
| - | ====Movimiento sobre un plano====
| + | |
| - | | + | |
| - | <math>\vec v = v_x\vec i + v_y\vec j</math>
| + | |
| - | | + | |
| - | <math>\vec v = \lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t} \vec i + \lim_{\Delta t\to 0}\frac{\Delta y}{\Delta t} \vec j</math>
| + | |
| - | | + | |
| - | Como se verá en su momento, el moviendo sobre el plano, podrá estudiarse analizando de modo independiente las variaciones de las componentes <math>r_x</math> y <math>r_y</math> del vector posición de la partícula <math>\vec r</math>, que nos informarán acerca de las componentes <math>v_x</math> y <math>v_y</math> vector velocidad <math>\vec v</math>.
| + | |
| - | | + | |
| - | | + | |
| - | Ir a [[Aceleración]].
| + | |
| - | | + | |
| - | [[Category:Física]]
| + | |
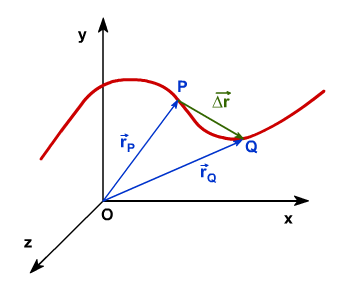
La velocidad se puede definir como la variación temporal de la posición del punto material
Este cociente nos define lo que llamamos velocidad media. Si consideramos que
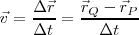
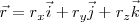
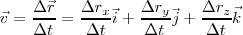
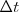 , obtenemos:
, obtenemos:
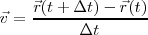
Aquí inserta texto sin formato--200.121.198.207 23:30 13 ago 2008 (CEST)