Navegación
Curvas cónicas
De Wikillerato
(Inserción de ejercicios resueltos en "Enlaces Externos") |
|||
| Línea 29: | Línea 29: | ||
[[Imagen:40Curvasconicas.gif]] | [[Imagen:40Curvasconicas.gif]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Enlaces Externos== | ||
| + | |||
| + | ;Problemas de Selectividad resueltos: | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=573 Asintotas de una hipérbola definida por sus focos y un punto P de la misma] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=574 Asíntotas de una hipérbola definida por sus focos y una tangente t] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=901 Circunferencia tangente a una recta] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=882 Circunferencias tangentes comunes a una recta y a otra circunferencia, conociendo el punto de tangencia T] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=201 Intersección de una recta con una elipse] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=200 Intersección recta-parábola] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=198 Parábola definida por la directriz y dos rectas tangentes] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=728 Parábola definida por su foco, una tangente y el eje] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=575 Parábola definida por su foco, una tangente y el punto de tangencia] | ||
| + | :[http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=5&idProblema=199 Rectas tangentes a una elipse desde un punto exterior a la curva] | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión de 11:43 5 sep 2008
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Características generales
Las curvas cónicas son las secciones planas de un cono de revolución.
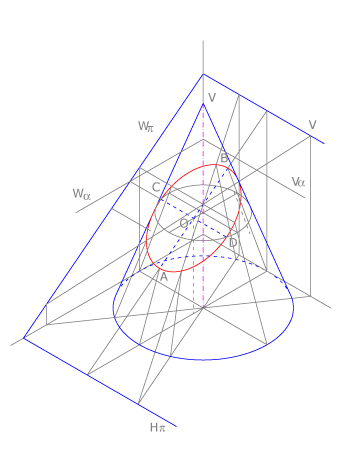
Elipses
La elipse es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es oblicuo al eje y a las generatrices.
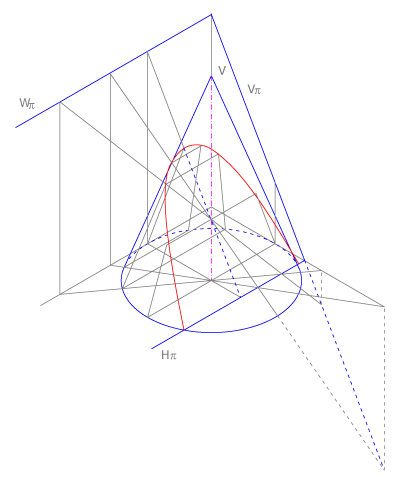
Parábolas
La parábola es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es paralelo a una de las generatrices.
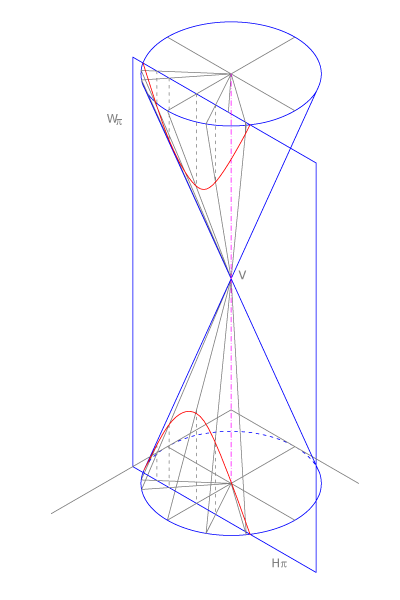
Hipérbolas
La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono.
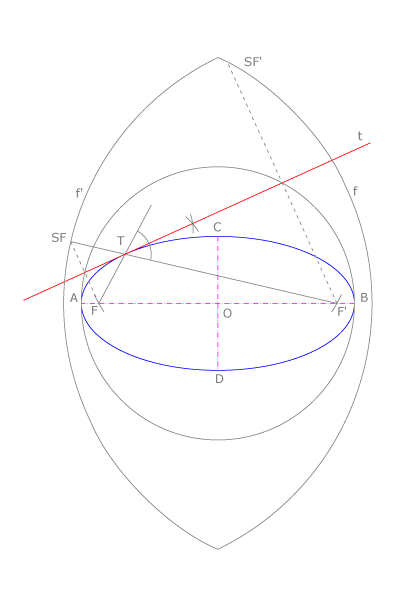
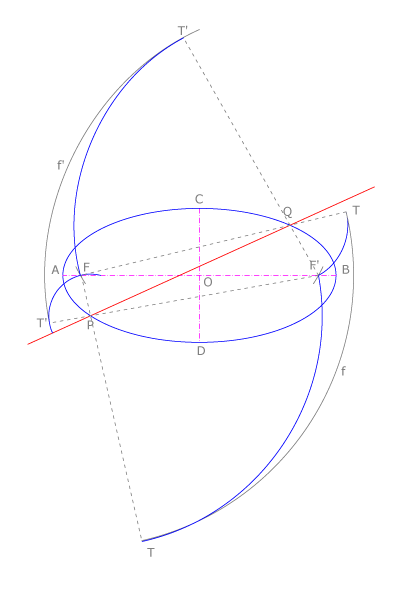
Rectas tangentes a las cónicas
La recta 
tangente a una cónica en un punto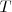 
de la misma es bisectriz del ángulo 
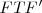, siendo 
y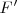 
los focos de la curva. El punto 
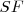, simétrico del foco respecto está sobre la circunferencia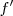 
, focal de 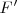. Del mismo modo, 
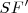está sobre 
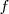, focal de .
Intersecciones de rectas y cónicas
Los puntos 
y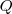 
, intersección de la recta 
con una cónica, son los centros de las circunferencias que pasan por uno de los focos y son tangentes a la focal del otro foco.
En la figura vemos que es centro de dos circunferencias: la que pasa por y es tangente en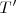 
a la focal de 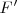y la que pasa por 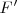y es tangente en 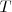a la focal de . Sucede otro tanto con .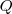
Enlaces Externos
- Problemas de Selectividad resueltos
- Asintotas de una hipérbola definida por sus focos y un punto P de la misma
- Asíntotas de una hipérbola definida por sus focos y una tangente t
- Circunferencia tangente a una recta
- Circunferencias tangentes comunes a una recta y a otra circunferencia, conociendo el punto de tangencia T
- Intersección de una recta con una elipse
- Intersección recta-parábola
- Parábola definida por la directriz y dos rectas tangentes
- Parábola definida por su foco, una tangente y el eje
- Parábola definida por su foco, una tangente y el punto de tangencia
- Rectas tangentes a una elipse desde un punto exterior a la curva
