Paralelismo
De Wikillerato
(→Trazado de las rectas paralelas a la recta s a la distancia d) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | ===Definición=== | ||
| + | |||
Dos rectas coplanarias r y s que no tengan ningún punto en común se llaman paralelas. | Dos rectas coplanarias r y s que no tengan ningún punto en común se llaman paralelas. | ||
| Línea 10: | Línea 12: | ||
Recordamos que la distancia en geometría es siempre la distancia menor. La distancia entre dos rectas paralelas se mide sobre una recta perpendicular a ambas. | Recordamos que la distancia en geometría es siempre la distancia menor. La distancia entre dos rectas paralelas se mide sobre una recta perpendicular a ambas. | ||
| - | Por dos puntos arbitrarios de la recta s trazamos dos rectas perpendiculares a ella y llevamos sobre cada una la magnitud '''d'''. Unimos los puntos obtenidos y así tenemos las rectas '''r y | + | Por dos puntos arbitrarios de la recta s trazamos dos rectas perpendiculares a ella y llevamos sobre cada una la magnitud '''d'''. Unimos los puntos obtenidos y así tenemos las rectas '''r y p''' buscadas. |
[[Imagen:DibujoTecnico I-1 13.gif]] | [[Imagen:DibujoTecnico I-1 13.gif]] | ||
| Línea 37: | Línea 39: | ||
[[Imagen:DibujoTecnico I-1 18.gif]] | [[Imagen:DibujoTecnico I-1 18.gif]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Tabla de contenidos |
Definición
Dos rectas coplanarias r y s que no tengan ningún punto en común se llaman paralelas.
Vamos a ver varios métodos de trazar rectas paralelas entre sí. Más adelante, en los capítulos dedicados a la historia del dibujo técnico, veremos que el quinto postulado de Euclides, referente a las paralelas, tiene una gran importancia pues es la clave para el nacimiento de otras geometrías.
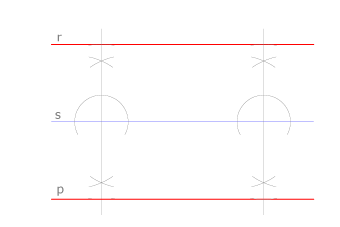
Trazado de las rectas paralelas a la recta s a la distancia d
Recordamos que la distancia en geometría es siempre la distancia menor. La distancia entre dos rectas paralelas se mide sobre una recta perpendicular a ambas. Por dos puntos arbitrarios de la recta s trazamos dos rectas perpendiculares a ella y llevamos sobre cada una la magnitud d. Unimos los puntos obtenidos y así tenemos las rectas r y p buscadas.
Trazado de la recta p paralela a r que pase por un punto P
Vamos a resolver este problema por dos métodos:
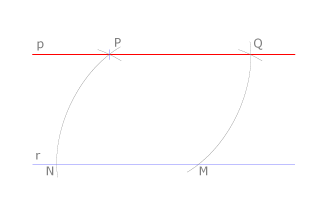
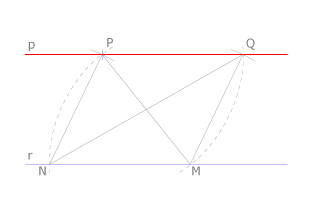
Aplicando el concepto de paralelogramo
Con centro en M, punto arbitrario de la recta dada, se traza un arco de radio MP que corta a la recta en el punto N. Con centro en P se traza un arco de igual radio, que pasará por M. Se mide con el compás la magnitud NP, trazando un arco de centro N y radio NP. Se traslada dicha magnitud al arco que pasa por M, trazando un arco de radio NP y centro M, que lo corta en el punto Q. La recta PQ es la recta p buscada, ya que MNPQ es un paralelogramo.
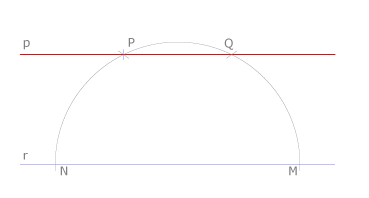
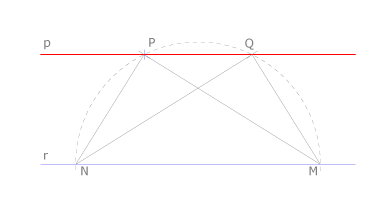
Aplicando el concepto de trapecio isósceles
Por un punto arbitrario de la recta r dada se traza una semicircunferencia que pase por P y que corta a dicha recta en M y N.
Se mide la magnitud NP trazando un arco de centro N y radio P. Con radio NP se traza otro arco con centro en M que corta a la semicircunferencia en Q. PQ es la recta p buscada, ya que MNPQ es un trapecio isósceles, único tipo de trapecio que puede inscribirse en una circunferencia y que tiene los lados no paralelos iguales.
Tweet