Ángulos
De Wikillerato
(→Con regla y compás) |
(→Dibujo de ángulos) |
||
| (80 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | ===Definición=== | ||
| + | |||
Un ángulo <math>\alpha</math> es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo. | Un ángulo <math>\alpha</math> es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo. | ||
| Línea 5: | Línea 7: | ||
===Nomenclatura de los ángulos=== | ===Nomenclatura de los ángulos=== | ||
Cuando un ángulo es menor de 90º se llama '''agudo''', si es mayor de 90º se llama '''obtuso''' y si mide 90º se llama '''recto'''. | Cuando un ángulo es menor de 90º se llama '''agudo''', si es mayor de 90º se llama '''obtuso''' y si mide 90º se llama '''recto'''. | ||
| - | El ángulo '''llano''' mide 180º, el ángulo completo 360º y el ángulo '''nulo''' 0º. | + | El ángulo '''llano''' o '''extendido''' mide 180º, el ángulo completo 360º y el ángulo '''nulo''' 0º. |
Dos ángulos se llaman '''suplementarios''' si suman 180º y '''complementarios''' si suman 90º. | Dos ángulos se llaman '''suplementarios''' si suman 180º y '''complementarios''' si suman 90º. | ||
| Línea 35: | Línea 37: | ||
[[Imagen:DibujoTecnico I-1 22.gif]] | [[Imagen:DibujoTecnico I-1 22.gif]] | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
===Bisectriz de un ángulo=== | ===Bisectriz de un ángulo=== | ||
| Línea 70: | Línea 65: | ||
[[Imagen:DibujoTecnico I-1 27.gif]] | [[Imagen:DibujoTecnico I-1 27.gif]] | ||
| - | = | + | aq6GPX <a href="http://bulodqmzdzua.com/">bulodqmzdzua</a>, [url=http://ywacussuaxgi.com/]ywacussuaxgi[/url], [link=http://qynuzkywybwf.com/]qynuzkywybwf[/link], http://pmznnzyairof.com/ |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
===Ángulo formado por dos circunferencias=== | ===Ángulo formado por dos circunferencias=== | ||
| - | Es el formado por las tangentes t y g en uno de los puntos de intersección, M o N. | + | Es el formado por las tangentes '''t y g''' en uno de los puntos de intersección, '''M o N'''. |
[[Imagen:DibujoTecnico I-1 34.gif]] | [[Imagen:DibujoTecnico I-1 34.gif]] | ||
| - | Si el ángulo entre dos circunferencias es de 90º, las circunferencias se llaman ortogonales. | + | Si el ángulo entre dos circunferencias es de '''90º''', las circunferencias se llaman '''ortogonales'''. |
[[Imagen:DibujoTecnico I-1 35.gif]] | [[Imagen:DibujoTecnico I-1 35.gif]] | ||
| Línea 126: | Línea 79: | ||
===La circunferencia. Nomenclatura=== | ===La circunferencia. Nomenclatura=== | ||
| - | La circunferencia c con centro en C es el lugar geométrico de los puntos del plano que equidistan del punto C. La distancia es el radio r de la circunferencia y se dibuja uniendo cualquier punto de ella con su centro C. | + | La '''circunferencia c''' con '''centro''' en '''C''' es el lugar geométrico de los puntos del plano que equidistan del punto '''C'''. La distancia es el '''radio r''' de la circunferencia y se dibuja uniendo cualquier punto de ella con su centro '''C'''. |
| - | Cuando dos circunferencias tienen el mismo centro se llaman concéntricas. | + | Cuando dos circunferencias tienen el mismo centro se llaman [[Circunferencias concéntricas|concéntricas]]. |
| - | Dos circunferencias pueden ser exteriores, secantes o tangentes. En el primer caso no tienen ningún punto común, en el segundo se cortan en dos puntos y en el tercero en un punto que se considera un punto doble. | + | Dos circunferencias pueden ser '''exteriores, secantes o tangentes'''. En el primer caso no tienen ningún punto común, en el segundo se cortan en dos puntos y en el tercero en un punto que se considera un punto doble. |
| - | Con respecto a una circunferencia c, con centro en C, una recta puede ser exterior, como e, secante como s y tangente como t. | + | Con respecto a una circunferencia '''c''', con centro en '''C''', una recta puede ser '''exterior''', como '''e, secante''' como '''s''' y '''tangente''' como '''t'''. |
| - | La recta t es tangente en el punto de tangencia T y el radio CT será perpendicular a t. | + | |
| - | Dos puntos M y N de la circunferencia definen sobre ella dos arcos, MHN y MTN. | + | La recta '''t''' es tangente en el '''punto de tangencia T''' y el radio '''CT''' será perpendicular a '''t'''. |
| - | M y N también definen un segmento rectilíneo MN interior a la circunferencia, que se llama cuerda. El radio CN que pasa por el punto medio F de una cuerda es perpendicular a ella y define el segmento FH que se llama flecha de una cuerda. | + | Dos puntos '''M y N''' de la circunferencia definen sobre ella dos '''arcos, MHN y MTN'''. |
| - | Cuando una cuerda pasa por C se llama diámetro de la circunferencia, como DE. | + | '''M y N''' también definen un segmento rectilíneo '''MN''' interior a la circunferencia, que se llama '''cuerda'''. El radio '''CN''' que pasa por el punto medio '''F''' de una cuerda es perpendicular a ella y define el segmento '''FH''' que se llama '''flecha''' de una cuerda. |
| + | Cuando una cuerda pasa por C se llama '''diámetro''' de la circunferencia, como '''DE'''. | ||
[[Imagen:DibujoTecnico I-1 36.gif]] | [[Imagen:DibujoTecnico I-1 36.gif]] | ||
| - | = | + | 7WUSZp <a href="http://xmkvapsfjett.com/">xmkvapsfjett</a>, [url=http://eamwpyucdfiw.com/]eamwpyucdfiw[/url], [link=http://knhojgahrmda.com/]knhojgahrmda[/link], http://ayfylqdhegyq.com/ |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[ | + | |
Revisión actual
Tabla de contenidos |
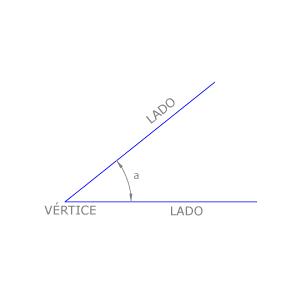
Definición
Un ángulo 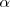 es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo.
es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo.
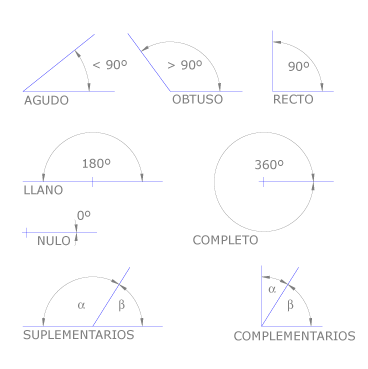
Nomenclatura de los ángulos
Cuando un ángulo es menor de 90º se llama agudo, si es mayor de 90º se llama obtuso y si mide 90º se llama recto. El ángulo llano o extendido mide 180º, el ángulo completo 360º y el ángulo nulo 0º. Dos ángulos se llaman suplementarios si suman 180º y complementarios si suman 90º.
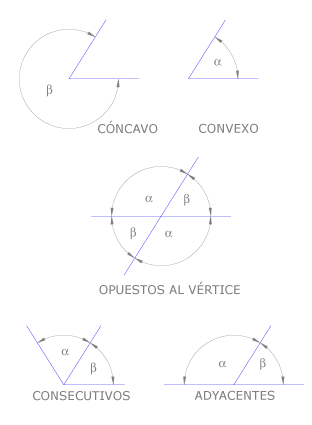
Un ángulo cóncavo mide más de 180º grados. Si se prolonga el lado de un ángulo cóncavo la prolongación divide al ángulo. Un ángulo convexo mide menos de 180º. Aunque se prolonguen sus lados las prolongaciones no dividen el ángulo. Cuando dos rectas se cortan forman cuatro ángulos iguales dos a dos y suplementarios dos a dos. Los que son iguales son opuestos al vértice. Dos ángulos son consecutivos cuando tienen un lado común. Dos ángulos son adyacentes cuando son consecutivos y suplementarios.
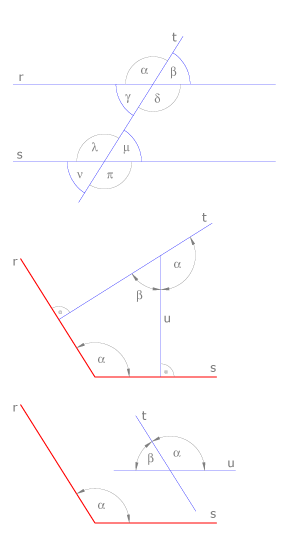
Cuando una recta corta a dos rectas paralelas se forman ángulos que tienen las siguientes características:
Todos tienen un lado común y otro lado en rectas paralelas entre sí.
Hay ángulos que son iguales por ser opuestos al vértice, como 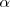 y
y 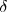 ; otros ángulos iguales se llaman alternos internos, como
; otros ángulos iguales se llaman alternos internos, como 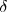 y
y 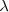 o alternos externos, como
o alternos externos, como 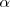 y
y  .
.
Propiedad relativa a los ángulos
Si se trazan dos rectas perpendiculares a los lados de un ángulo, éstas forman un ángulo igual al dado y otro suplementario. Si se trazan dos rectas paralelas a los lados de un ángulo éstas forman un ángulo igual al dado y otro suplementario.
Traslado de un ángulo
Si queremos dibujar un ángulo igual a uno dado con vértice en un punto dado A, dibujamos un arco de radio arbitrario con centro en el vértice del ángulo dado y otro arco igual con centro en A. Medimos con el compás el arco limitado por los lados del ángulo dado y llevamos tal medida con el compás sobre el arco de centro en A.
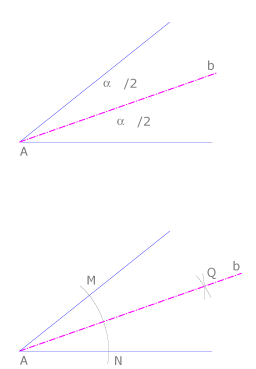
Bisectriz de un ángulo
Es la recta que divide un ángulo en dos partes iguales. La propiedad de cada uno de los puntos de una bisectriz es que equidista de los lados del ángulo. Para trazar una bisectriz se dibuja un arco de radio arbitrario con centro en el vértice. Este arco corta a los lados en los puntos M y N. La bisectriz b es la mediatriz de la cuerda MN.
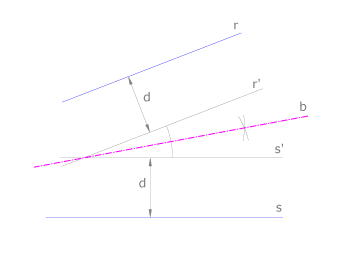
Bisectriz de dos rectas que se cortan fuera del dibujo. Vamos a resolver este problema por dos métodos:
1. Dibujamos dos rectas r’ y s’ paralelas a las dadas, r y s, de modo que la distancia d entre los dos pares de paralelas sea la misma.
La bisectriz b buscada es la bisectriz de r’ y s’.
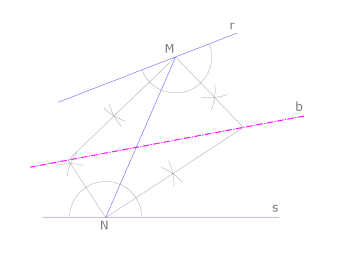
2. Dibujamos un segmento arbitrario MN que tenga un extremo en cada una de las rectas dadas, r y s. Trazamos las bisectrices de los ángulos en M y N. Estas bisectrices se cortan en puntos de la bisectriz b buscada, porque, por ser intersección de las bisectrices, cada uno de ellos es equidistante de las tres rectas.
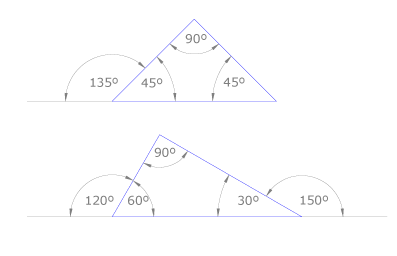
Ángulos de la escuadra y el cartabón
La escuadra es un triángulo rectángulo isósceles. Sus ángulos interiores son uno de 90º y dos de 45º. El cartabón es un triángulo rectángulo escaleno. Sus ángulos miden 90º, 60º y 30º.
aq6GPX <a href="http://bulodqmzdzua.com/">bulodqmzdzua</a>, [url=http://ywacussuaxgi.com/]ywacussuaxgi[/url], [link=http://qynuzkywybwf.com/]qynuzkywybwf[/link], http://pmznnzyairof.com/
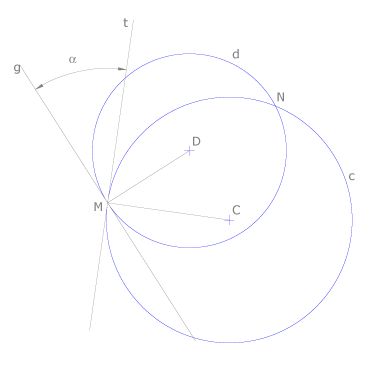
Ángulo formado por dos circunferencias
Es el formado por las tangentes t y g en uno de los puntos de intersección, M o N.
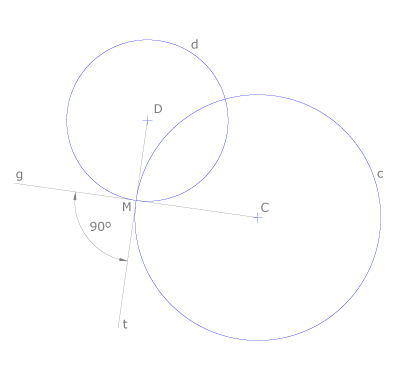
Si el ángulo entre dos circunferencias es de 90º, las circunferencias se llaman ortogonales.
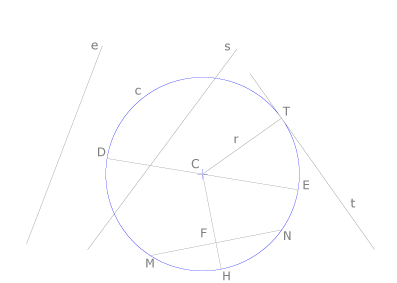
La circunferencia. Nomenclatura
La circunferencia c con centro en C es el lugar geométrico de los puntos del plano que equidistan del punto C. La distancia es el radio r de la circunferencia y se dibuja uniendo cualquier punto de ella con su centro C. Cuando dos circunferencias tienen el mismo centro se llaman concéntricas. Dos circunferencias pueden ser exteriores, secantes o tangentes. En el primer caso no tienen ningún punto común, en el segundo se cortan en dos puntos y en el tercero en un punto que se considera un punto doble. Con respecto a una circunferencia c, con centro en C, una recta puede ser exterior, como e, secante como s y tangente como t.
La recta t es tangente en el punto de tangencia T y el radio CT será perpendicular a t. Dos puntos M y N de la circunferencia definen sobre ella dos arcos, MHN y MTN. M y N también definen un segmento rectilíneo MN interior a la circunferencia, que se llama cuerda. El radio CN que pasa por el punto medio F de una cuerda es perpendicular a ella y define el segmento FH que se llama flecha de una cuerda. Cuando una cuerda pasa por C se llama diámetro de la circunferencia, como DE.
7WUSZp <a href="http://xmkvapsfjett.com/">xmkvapsfjett</a>, [url=http://eamwpyucdfiw.com/]eamwpyucdfiw[/url], [link=http://knhojgahrmda.com/]knhojgahrmda[/link], http://ayfylqdhegyq.com/
Tweet