Puntos y rectas notables de los triángulos
De Wikillerato
(→Las bisectrices) |
|||
| (55 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Puntos y rectas notables de los triángulos== | ==Puntos y rectas notables de los triángulos== | ||
| - | Las rectas y puntos notables de un triángulo <math>ABC</math> son: | + | Las rectas y puntos notables de un [[Triángulos| triángulo]] <math>ABC</math> son: |
las mediatrices, <math>m_{AB}, \ m_{AC}, \ m_{BC}</math>, que se cortan en un punto llamado circuncentro <math>C</math> ,centro de la circunferencia circunscrita al triángulo; | las mediatrices, <math>m_{AB}, \ m_{AC}, \ m_{BC}</math>, que se cortan en un punto llamado circuncentro <math>C</math> ,centro de la circunferencia circunscrita al triángulo; | ||
| - | las medianas, <math>n_A ,n_B , n_C</math>, que se cortan en el baricentro, <math>B</math>, centro de gravedad del triángulo; | + | las [[Mediana| medianas]], <math>n_A ,n_B , n_C</math>, que se cortan en el baricentro, <math>B</math>, centro de gravedad del triángulo; |
las bisectrices, <math>b_A ,b_B , b_C</math>, que se cortan en el incentro <math>I</math>, centro de la circunferencia inscrita del triángulo; | las bisectrices, <math>b_A ,b_B , b_C</math>, que se cortan en el incentro <math>I</math>, centro de la circunferencia inscrita del triángulo; | ||
| Línea 64: | Línea 64: | ||
[[Imagen:DibujoTecnico_I-2_21.gif]] | [[Imagen:DibujoTecnico_I-2_21.gif]] | ||
| - | + | ===Las bisectrices=== | |
| - | + | ||
Las bisectrices de los ángulos interiores de un triángulo <math>ABC</math> se cortan en un punto llamado '''incentro''' que siempre es interior al triángulo. Como el '''incentro''' <math>I</math> pertenece a las tres bisectrices equidista de los tres lados y es el centro de la circunferencia inscrita a <math>ABC</math>. | Las bisectrices de los ángulos interiores de un triángulo <math>ABC</math> se cortan en un punto llamado '''incentro''' que siempre es interior al triángulo. Como el '''incentro''' <math>I</math> pertenece a las tres bisectrices equidista de los tres lados y es el centro de la circunferencia inscrita a <math>ABC</math>. | ||
Revisión actual
Tabla de contenidos |
Puntos y rectas notables de los triángulos
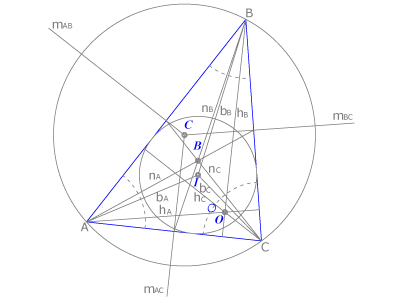
Las rectas y puntos notables de un triángulo  son:
son:
las mediatrices, 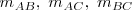 , que se cortan en un punto llamado circuncentro
, que se cortan en un punto llamado circuncentro  ,centro de la circunferencia circunscrita al triángulo;
,centro de la circunferencia circunscrita al triángulo;
las medianas, 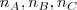 , que se cortan en el baricentro,
, que se cortan en el baricentro, 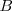 , centro de gravedad del triángulo;
, centro de gravedad del triángulo;
las bisectrices, 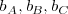 , que se cortan en el incentro
, que se cortan en el incentro 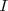 , centro de la circunferencia inscrita del triángulo;
, centro de la circunferencia inscrita del triángulo;
las alturas, 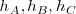 , que se cortan en el ortocentro,
, que se cortan en el ortocentro, 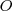 .
.
Las mediatrices
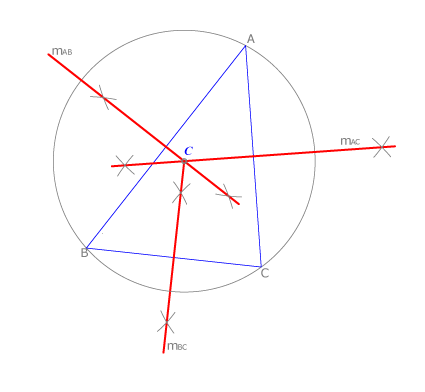
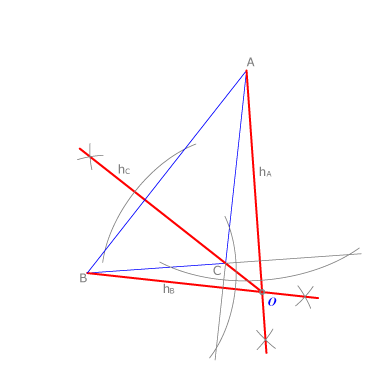
Las mediatrices de un triángulo acutángulo se cortarán siempre en un punto interior del triángulo, luego su circuncentro será interior al triángulo.
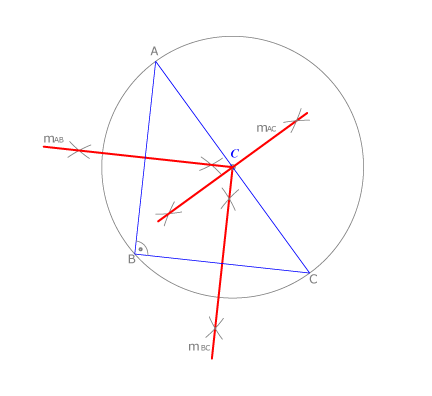
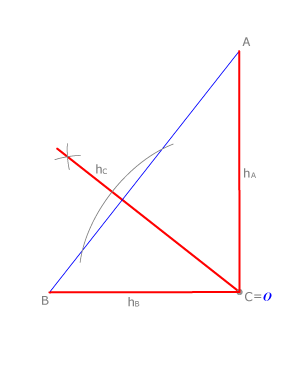
En el caso del triángulo rectángulo vemos que el circuncentro coincide con el punto medio de la hipotenusa.
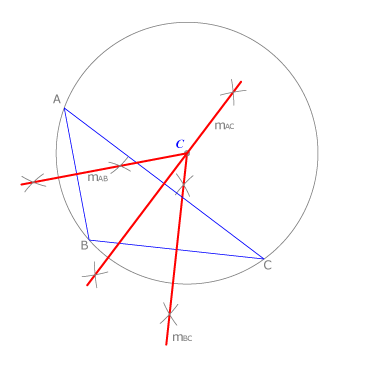
En el caso de un triángulo obtusángulo, el circuncentro es exterior al triángulo.
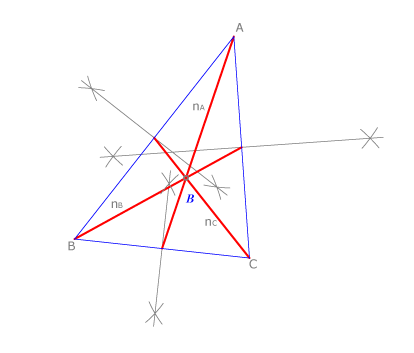
Las medianas
Las medianas se cortan siempre en un punto interior del triángulo.
El baricentro tiene una propiedad física importante: es el centro de gravedad del triángulo.
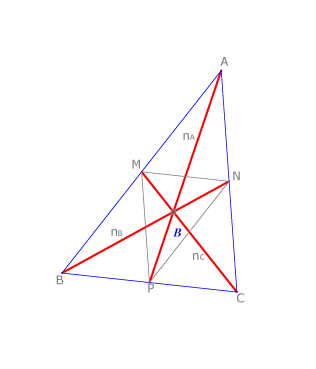
Si unimos los puntos medios de los lados del triángulo  obtenemos el triángulo
obtenemos el triángulo 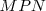 que tiene el mismo baricentro que
que tiene el mismo baricentro que  y sus medianas miden la mitad que las de
y sus medianas miden la mitad que las de  .
.
Además los lados de 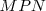 miden la mitad que los lados de
miden la mitad que los lados de  y la superficie de
y la superficie de 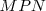 es la cuarta parte de la superficie de
es la cuarta parte de la superficie de  , pues podemos comprobar que al trazar
, pues podemos comprobar que al trazar 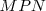 se han definido otros tres triángulos iguales:
se han definido otros tres triángulos iguales: 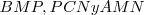 .
.
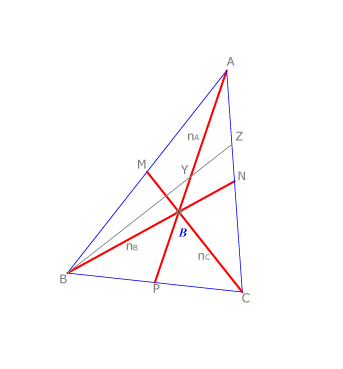
Consideramos una mediana 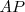 . Si
. Si 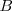 es el baricentro se cumple que
es el baricentro se cumple que 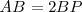 .
.
Se cumple también que si se dibuja 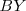 , la mediana de la mediana
, la mediana de la mediana 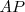 , ésta corta al lado
, ésta corta al lado 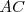 siendo:
siendo: 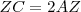 .
.
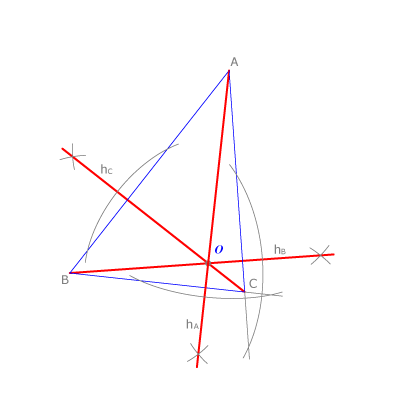
Las alturas
Las alturas de un triángulo acutángulo se cortan siempre en un punto interior del triángulo, luego su ortocentro es interior al triángulo.
En el caso de un triángulo obtusángulo, el ortocentro es exterior al triángulo.
En el caso del triángulo rectángulo vemos que el ortocentro coincide con el vértice del ángulo recto.
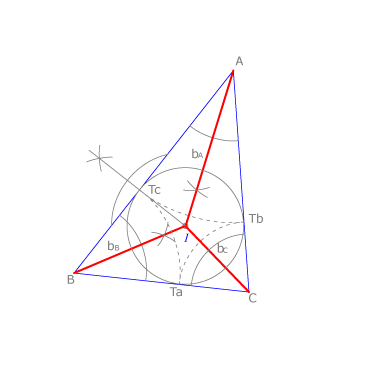
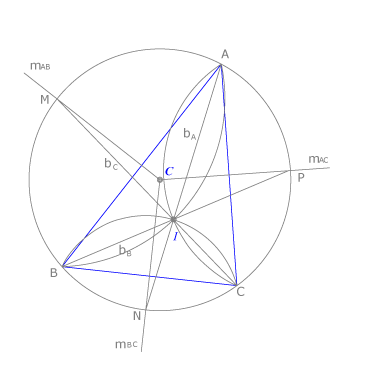
Las bisectrices
Las bisectrices de los ángulos interiores de un triángulo  se cortan en un punto llamado incentro que siempre es interior al triángulo. Como el incentro
se cortan en un punto llamado incentro que siempre es interior al triángulo. Como el incentro 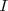 pertenece a las tres bisectrices equidista de los tres lados y es el centro de la circunferencia inscrita a
pertenece a las tres bisectrices equidista de los tres lados y es el centro de la circunferencia inscrita a  .
.
Para dibujar dicha circunferencia debemos hallar los puntos de tangencia sobre los lados. Basta con trazar una perpendicular desde 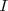 a uno de ellos, por ejemplo al lado
a uno de ellos, por ejemplo al lado  , obteniendo
, obteniendo 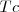 y, a continuación trasladar el resultado a cada uno de los lados del triángulo, como se ve en la figura, ya que
y, a continuación trasladar el resultado a cada uno de los lados del triángulo, como se ve en la figura, ya que 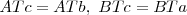 y
y 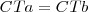 .
.
El teorema de la bisectriz dice que “la bisectriz de un ángulo interno corta al lado opuesto en partes proporcionales a los otros lados”.
Demostraremos este teorema al ocuparnos de la proporcionalidad directa.
Propiedades relativas a las rectas y puntos notables de los triángulos
Suma de vectores
En un triángulo  , cuyo circuncentro es
, cuyo circuncentro es  y su ortocentro es
y su ortocentro es 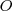 , se verifica que el vector
, se verifica que el vector 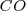 es igual a la suma de los vectores
es igual a la suma de los vectores 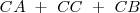 .
.
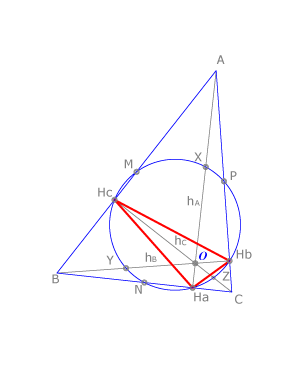
Triángulo órtico y circunferencia de Feuerbach
El triángulo 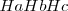 que tiene como vértices los pies de las alturas de un triángulo
que tiene como vértices los pies de las alturas de un triángulo  se llama triángulo órtico.
se llama triángulo órtico.
Las bisectrices del triángulo órtico de  están en las mismas rectas que contienen a las alturas de dicho triángulo.
están en las mismas rectas que contienen a las alturas de dicho triángulo.
La circunferencia circunscrita al órtico de  se llama circunferencia de Feuerbach o circunferencia de los nueve puntos ya que pasa también por los puntos medios de los lados de
se llama circunferencia de Feuerbach o circunferencia de los nueve puntos ya que pasa también por los puntos medios de los lados de 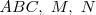 y
y  y por los puntos medios de los segmentos que unen el ortocentro con los vértices de
y por los puntos medios de los segmentos que unen el ortocentro con los vértices de 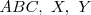 y
y 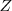 .
.
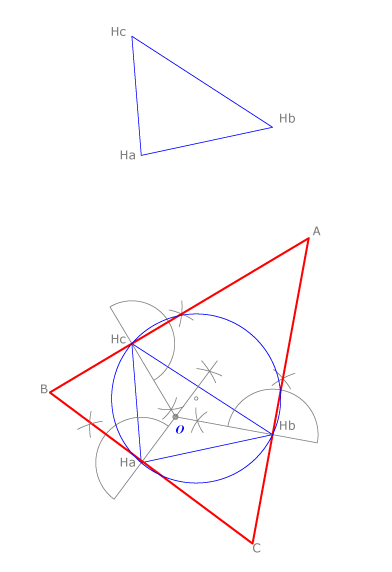
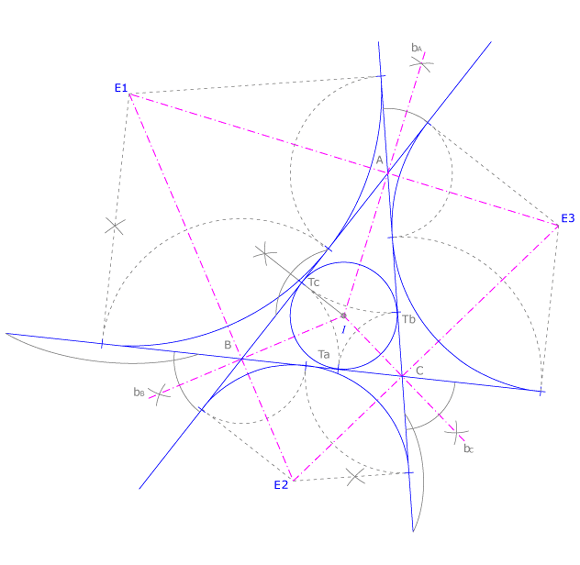
Sea 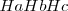 es el triángulo órtico de un triángulo desconocido
es el triángulo órtico de un triángulo desconocido  . Al hallar
. Al hallar  vamos a ver que existen cuatro soluciones, lo que indica que cada órtico y cada circunferencia de Feuerbach pueden pertenecer a cuatro triángulos distintos.
vamos a ver que existen cuatro soluciones, lo que indica que cada órtico y cada circunferencia de Feuerbach pueden pertenecer a cuatro triángulos distintos.
Dibujamos las bisectrices de  , que coinciden con las alturas de
, que coinciden con las alturas de  . Trazamos por
. Trazamos por 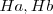 y
y 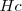 perpendiculares a tales bisectrices, que son los lados del triángulo buscado,
perpendiculares a tales bisectrices, que son los lados del triángulo buscado,  . Esta es la primera solución. Señalamos el ortocentro
. Esta es la primera solución. Señalamos el ortocentro 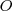 y la circunferencia de Feuerbach.
y la circunferencia de Feuerbach.
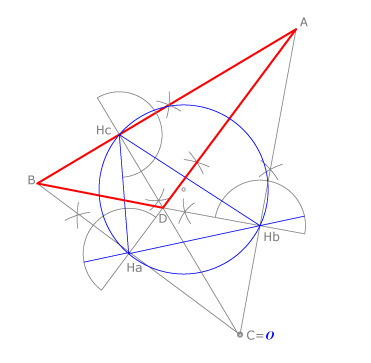
Las otras soluciones son los tres triángulos obtusángulos que obtenemos al considerar como lados las alturas de  , como
, como 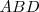 , cuyo ortocentro coincide con el vértice
, cuyo ortocentro coincide con el vértice  . Las otras soluciones serían
. Las otras soluciones serían 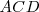 , con ortocentro en
, con ortocentro en 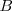 y
y 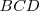 , con ortocentro en
, con ortocentro en  .
.
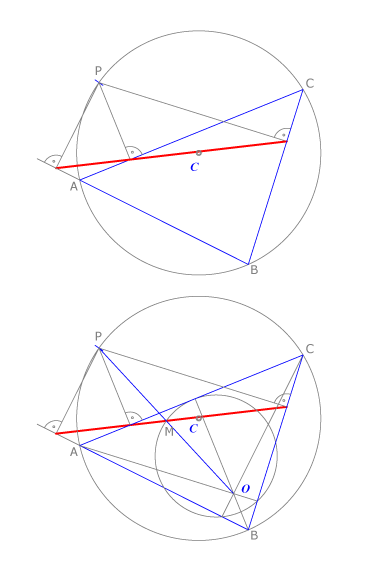
Recta de Simson
Sea un triángulo  y su circunferencia circunscrita. Si trazamos rectas perpendiculares a los lados de
y su circunferencia circunscrita. Si trazamos rectas perpendiculares a los lados de  desde un punto arbitrario
desde un punto arbitrario  de la circunferencia, los pies de dichas perpendiculares están alineados en una recta que se llama recta de Simson.
de la circunferencia, los pies de dichas perpendiculares están alineados en una recta que se llama recta de Simson.
Si unimos  con el ortocentro de
con el ortocentro de  el punto medio
el punto medio 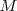 del segmento obtenido está sobre la recta de Simson y sobre la circunferencia de Feuerbach de
del segmento obtenido está sobre la recta de Simson y sobre la circunferencia de Feuerbach de  .
.
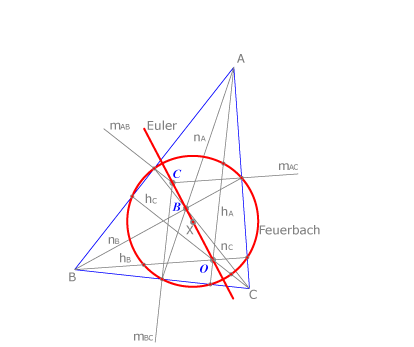
Recta de Euler
La recta definida por el circuncentro y el ortocentro de un triángulo  se llama recta de Euler. La recta de Euler contiene también al baricentro y al centro de la circunferencia de Feuerbach,
se llama recta de Euler. La recta de Euler contiene también al baricentro y al centro de la circunferencia de Feuerbach, 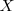 .
.
La distancia entre el baricentro y el circuncentro es la mitad de la distancia entre el baricentro y el ortocentro: 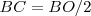 .
.
El centro de la circunferencia de Feuerbach es el punto medio de 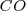 , segmento definido por el circuncentro y el ortocentro.
, segmento definido por el circuncentro y el ortocentro.
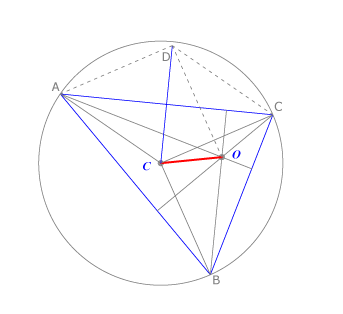
Propiedad de las mediatrices y las bisectrices
Sea un triángulo  . La bisectriz de cada ángulo se corta con la mediatriz del lado opuesto en un punto de la circunferencia circunscrita.
. La bisectriz de cada ángulo se corta con la mediatriz del lado opuesto en un punto de la circunferencia circunscrita.
Circunferencia exinscritas y exincentros de un triángulo
Trazamos las bisectrices de los ángulos exteriores de un triángulo  .
.
Estas bisectrices serán perpendiculares en cada vértice a las bisectrices del ángulo interior del mismo, ya que los ángulos son suplementarios. Se cortarán dos a dos en tres puntos llamados exincentros que son los centros de las tres circunferencias exinscritas al triángulo.
Estas circunferencias son tangentes a las tres rectas definidas por los vértices 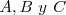 .
.
El triángulo definido por los exincentros tiene como triángulo órtico a  .
.
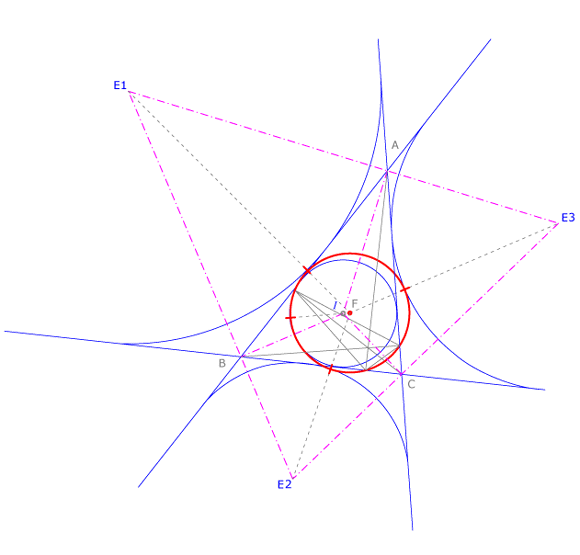
Teorema de Feuerbach
El teorema de Feuerbach dice: “La circunferencia de Feuerbach de un triángulo  es tangente común a la circunferencia inscrita y a las tres circunferencias exinscritas de
es tangente común a la circunferencia inscrita y a las tres circunferencias exinscritas de  ”.
”.
Para comprobarlo trazamos dichas circunferencias y hallamos los puntos de tangencia respectivos uniendo ordenadamente sus centros.
Tweet