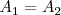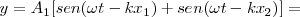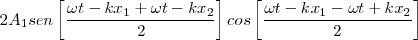Interferencias
De Wikillerato
(→Puntos de interferencia constructiva) |
|||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 27: | Línea 27: | ||
Movimientos en concordancia de fase. | Movimientos en concordancia de fase. | ||
| - | + | [[Imagen:interferencias5.gif]] | |
Movimientos en oposición de fase | Movimientos en oposición de fase | ||
| Línea 54: | Línea 54: | ||
| - | + | [[Imagen:Interferencias4.jpg]] | |
| Línea 60: | Línea 60: | ||
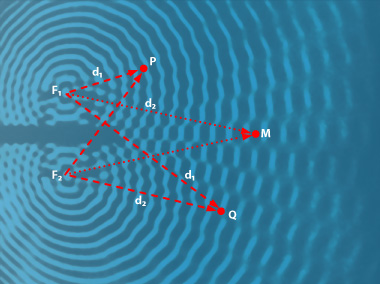
Todos los puntos de la banda central son equidistantes de <math>F_1</math> y <math>F_2</math>, es decir, <math>d1 - d2 = 0</math>, siendo <math>d1</math> y <math>d2</math> las distancias del punto <math>M</math> considerado a <math>F_1 y F_2</math> respectivamente. | Todos los puntos de la banda central son equidistantes de <math>F_1</math> y <math>F_2</math>, es decir, <math>d1 - d2 = 0</math>, siendo <math>d1</math> y <math>d2</math> las distancias del punto <math>M</math> considerado a <math>F_1 y F_2</math> respectivamente. | ||
| + | |||
| + | Los puntos de iluminación brillante, tales como <math>P</math>, se corresponderán con zonas de máxima amplitud, es decir, las crestas de las ondas resultantes. Si contamos detenidamente las circunferencias brillantes que parten de <math>F_1</math>, vemos que <math>d_1 = 7 \lambda</math> en este caso, y, contando las que parten de <math>F_2</math> , obtenemos que <math>d_2 = 11 \lambda</math>. | ||
| + | |||
| + | La diferencia de esa franja es <math>\vert d1 - d2 \vert = 4 \lambda</math>, cantidad constante. Es decir, que todas las zonas brillantes se corresponden con una diferencia que es un múltiplo entero de <math>\lambda</math>, o lo que es igual <math>\vert d1 - d2 \vert = n \lambda</math>, con <math>n</math> perteneciente a <math>N</math>. | ||
| + | |||
| + | En esas franjas, donde coinciden las crestas de los movimientos ondulatorios individuales, la amplitud resultante será la suma de las amplitudes de ambos movimientos ondulatorios, se produce una superposición constructiva. y diremos que se trata de '''interferencias constructivas'''. | ||
| + | |||
| + | Iguales consideraciones se pueden hacer para las franjas negras. En este caso, los valles de ambas ondas coinciden, la amplitud resultante será igual a la suma de la amplitud de los valles de ambos movimientos ondulatorios. Se trata también de '''interferencias constructivas'''. | ||
| + | |||
| + | Hipérbolas cuyos puntos <math>Q</math> permanecen inmóviles, en los que observamos que, como en este caso, <math>\vert d_1 - d_2 \vert = (2n - 1) \frac{\lambda}{2}</math> | ||
| + | |||
| + | con <math>n</math> perteneciente a <math>N</math>, pues | ||
| + | |||
| + | <math>d_1 = 13,5 \lambda</math> | ||
| + | |||
| + | y | ||
| + | |||
| + | <math>d_2 = 12 \lambda</math>, | ||
| + | |||
| + | con lo cual | ||
| + | |||
| + | |||
| + | <math>\vert d1 - d2 \vert = 1,5\lambda </math>, | ||
| + | |||
| + | o lo que es igual, <math>3 \frac{\lambda }{2}</math>. | ||
| + | |||
| + | En esos puntos coinciden exactamente las crestas de uno de los movimientos con los valles del otro, la suma de las amplitudes se hace cero, por lo cual los puntos permanecen inmóviles, se producen interferencias destructivas. | ||
| + | |||
| + | Pero veamos la demostración analítica de esas observaciones. | ||
| + | |||
| + | ===Puntos de interferencia constructiva=== | ||
| + | |||
| + | Consideremos las ecuaciones de ambos movimientos. Dado que las dos fuentes producen movimientos de igual frecuencia y en concordancia de fase, es decir, son coherentes y, además, de igual amplitud, tendremos: | ||
| + | |||
| + | <math>y_1 = A_1 sen (\omega t - k x_1) </math> | ||
| + | |||
| + | <math>y = y_1 + y_2 = A_1 sen (\omega t - k x_1) + A_2 sen (\omega t - k x_2) </math> | ||
| + | |||
| + | <math>y_2 = A_2 sen (\omega t - k x_2) </math> | ||
| + | |||
| + | pero como <math>A_1 = A_2</math> | ||
| + | |||
| + | |||
| + | |||
| + | <math> y = A_1 \lbrack sen (\omega t - k x_1) + sen (\omega t - k x_2)\rbrack =</math> | ||
| + | |||
| + | <math>2 A_1 sen \left \lbrack \frac {\omega t - k x_1 +\omega t - k x_2}{2}\right \rbrack cos \left \lbrack \frac {\omega t - k x_1 -\omega t + k x_2}{2}\right \rbrack</math> | ||
| + | |||
| + | |||
| + | [[Categoría: Física]] | ||
Revisión actual
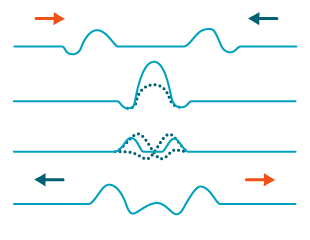
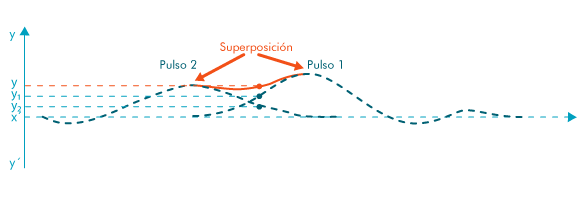
La superposición de dos pulsos
Para poder interpretar correctamente los fenómenos de propagación y de difracción de una onda progresiva, es necesario estudiar el fenómeno que resulta de la superposición de dos pulsos en un punto del medio donde se propagan. Si dos pulsos se cruzan en un medio transmisor sus efectos se superponen. La velocidad de cada uno de ellos se mantiene invariable, no queda afectada por ese encuentro y cada pulso continúa su propagación en la dirección que traía una vez que se hayan cruzado.
Esta afirmación, puede hacerse solamente para situaciones muy especiales: dos pulsos de pequeña amplitud y siempre que no se exceda el límite de elasticidad del medio. La elongación en el punto es la suma de las elongaciones que, en ese punto, tiene cada pulso y se conoce como Ley de superposición que se puede enunciar: Cuando varias ondas de pequeña amplitud, de una magnitud representada por y, se superponen en un instante dado en un punto P del medio de propagación, la variación de y en el punto es igual a la suma de las variaciones 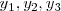 ,… que cada onda individualmente produciría en el punto.
,… que cada onda individualmente produciría en el punto.
Si producimos dos pulsos en una cubeta de ondas y estudiamos el corte vertical de la superficie del agua, se podrá observar que, después de producirse la superposición, cada pulso sigue su camino.
Interferencias en la superficie del agua
En una cubeta de ondas podremos observar la superposición de ondas que tienen dirección opuesta, observamos como en el segmento que separa ambos focos aparecen una serie de franjas brillantes y oscuras, que corresponderán a crestas y valles respectivamente. Pero fuera de ese segmento, se observan además franjas grises que corresponden a los puntos donde la superficie del agua aparece inmóvil.
El fenómeno de interferencias resulta de la superposición en un mismo punto de dos movimientos ondulatorios emitidos por dos focos coherentes, es decir, sus oscilaciones respectivas presentan entre sí una diferencia de fase constante.
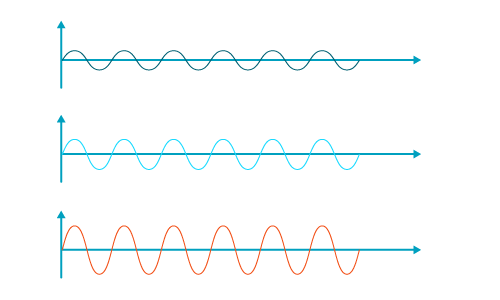
Movimientos en concordancia de fase.
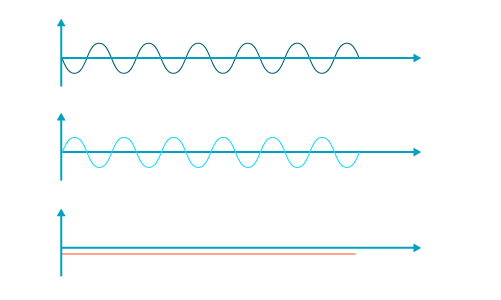
Movimientos en oposición de fase
Si en una cubeta de ondas, utilizamos un tubo que después se divide en forma de horquilla, cada punta produce sendas vibraciones. Sobre la capa de agua los movimientos ondulatorios generados por cada punta se superponen. En este caso, los movimientos son isocronos (igual frecuencia) sincronos (igualdad de fase) y, además, de igual amplitud.
En la pantalla de la cubeta de ondas, observamos una imagen estroboscópica en la que aparecen:
a) franjas muy brillantes, que se corresponderán a crestas más acentuadas que cuando sólo hay un movimiento ondulatorio sobre la capa de agua;
b) zonas muy oscuras, que se corresponderán con valles más acentuados;
c) bandas grises que se corresponden con zonas que permanecen en reposo.
Pero la forma que adoptan esas zonas es muy particular.
En primer lugar observamos una franja central, constituida por una sucesión de zonas brillantes y oscuras, que coincide con la mediatriz del segmento 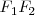 .
.
Alternándose con franjas de las mismas características, observamos además franjas inmóviles . Todas ellas tienen forma de ramas de hipérbolas, de modo que son simétricas con relación a la franja central y pasan todas ellas por el segmento 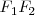 cortándolo de forma ortogonal.
cortándolo de forma ortogonal.
Debemos recordar aquí que se define una hipérbola como el lugar geométrico de los puntos cuyas distancias a dos puntos fijos se diferencian una cantidad constante.
Si queremos hallar una explicación del fenómeno debemos destacar inmediatamente:
Todos los puntos de la banda central son equidistantes de 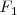 y
y 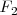 , es decir,
, es decir, 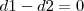 , siendo
, siendo 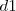 y
y 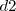 las distancias del punto
las distancias del punto 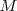 considerado a
considerado a 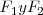 respectivamente.
respectivamente.
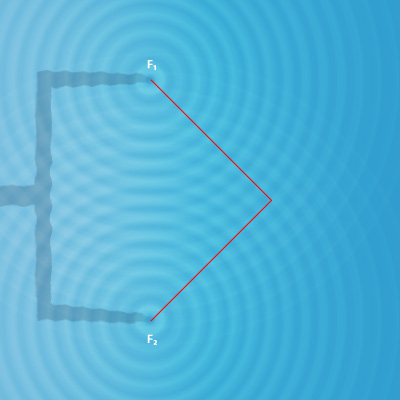
Los puntos de iluminación brillante, tales como  , se corresponderán con zonas de máxima amplitud, es decir, las crestas de las ondas resultantes. Si contamos detenidamente las circunferencias brillantes que parten de
, se corresponderán con zonas de máxima amplitud, es decir, las crestas de las ondas resultantes. Si contamos detenidamente las circunferencias brillantes que parten de 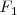 , vemos que
, vemos que 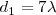 en este caso, y, contando las que parten de
en este caso, y, contando las que parten de 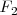 , obtenemos que
, obtenemos que 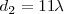 .
.
La diferencia de esa franja es 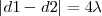 , cantidad constante. Es decir, que todas las zonas brillantes se corresponden con una diferencia que es un múltiplo entero de
, cantidad constante. Es decir, que todas las zonas brillantes se corresponden con una diferencia que es un múltiplo entero de 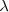 , o lo que es igual
, o lo que es igual 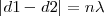 , con
, con  perteneciente a
perteneciente a 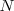 .
.
En esas franjas, donde coinciden las crestas de los movimientos ondulatorios individuales, la amplitud resultante será la suma de las amplitudes de ambos movimientos ondulatorios, se produce una superposición constructiva. y diremos que se trata de interferencias constructivas.
Iguales consideraciones se pueden hacer para las franjas negras. En este caso, los valles de ambas ondas coinciden, la amplitud resultante será igual a la suma de la amplitud de los valles de ambos movimientos ondulatorios. Se trata también de interferencias constructivas.
Hipérbolas cuyos puntos 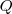 permanecen inmóviles, en los que observamos que, como en este caso,
permanecen inmóviles, en los que observamos que, como en este caso, 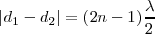
con  perteneciente a
perteneciente a 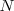 , pues
, pues
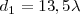
y
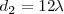 ,
,
con lo cual
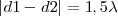 ,
,
o lo que es igual, 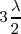 .
.
En esos puntos coinciden exactamente las crestas de uno de los movimientos con los valles del otro, la suma de las amplitudes se hace cero, por lo cual los puntos permanecen inmóviles, se producen interferencias destructivas.
Pero veamos la demostración analítica de esas observaciones.
Puntos de interferencia constructiva
Consideremos las ecuaciones de ambos movimientos. Dado que las dos fuentes producen movimientos de igual frecuencia y en concordancia de fase, es decir, son coherentes y, además, de igual amplitud, tendremos:
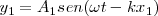

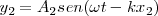
pero como