Navegación
Operaciones con sucesos
De Wikillerato
m (Revertidas las ediciones realizadas por 80.24.233.97 (Talk); a la última edición de 82.199.32.66) |
|||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Inclusión e igualdad de sucesos== | ==Inclusión e igualdad de sucesos== | ||
| - | |||
<br/> | <br/> | ||
| Línea 7: | Línea 6: | ||
A | A | ||
</math> | </math> | ||
| - | | + | está incluido (o contenido) en otro suceso |
<math> | <math> | ||
B | B | ||
</math> | </math> | ||
| - | si todo suceso elemental | + | si todo suceso elemental perteneciente a |
<math> | <math> | ||
A | A | ||
</math> | </math> | ||
| - | pertenece también a | + | , pertenece también a |
<math> | <math> | ||
B | B | ||
</math> | </math> | ||
| - | . | + | . Esta inclusión se representa por |
<math> | <math> | ||
A \subset B | A \subset B | ||
| Línea 27: | Línea 26: | ||
<br/> | <br/> | ||
| - | Dos | + | Dos sucesos |
<math> | <math> | ||
A | A | ||
| Línea 35: | Línea 34: | ||
B | B | ||
</math> | </math> | ||
| - | son iguales si están formados por los mismos sucesos elementales. Se representa | + | son iguales si están formados por los mismos sucesos elementales. Ocurre que: <math> |
| - | por | + | A \subset B |
| + | </math> y <math> | ||
| + | B \subset A | ||
| + | </math>. Se representa | ||
| + | por: | ||
<math> | <math> | ||
A = B | A = B | ||
| Línea 108: | Línea 111: | ||
B | B | ||
</math> | </math> | ||
| - | . Se representa por | + | . Este suceso intersección está formado por todos los sucesos elementales que pertenecen a |
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y a | ||
| + | <math> | ||
| + | B | ||
| + | </math>, al mismo tiempo. Se representa por | ||
<math> | <math> | ||
A \cap B | A \cap B | ||
</math> | </math> | ||
. | . | ||
| + | |||
| + | <br/> | ||
Cuando | Cuando | ||
<math> | <math> | ||
| - | A \ | + | A \cap B |
</math> | </math> | ||
| - | es el suceso imposible, decimos que los sucesos | + | es el suceso imposible, es decir, no hay ningún suceso elemental que pertenezca a A y a B al mismo tiempo, decimos que los sucesos |
<math> | <math> | ||
A | A | ||
| Línea 126: | Línea 138: | ||
B | B | ||
</math> | </math> | ||
| - | son incompatibles. | + | son incompatibles. Su intersección, como conjuntos, es igual al conjunto vacío. |
| + | (<math> A \cap B = \emptyset </math>) | ||
| + | |||
| + | En caso contrario, es decir, si la intersección es no vacía, decimos que | ||
<math> | <math> | ||
A | A | ||
| Línea 141: | Línea 156: | ||
<br/> | <br/> | ||
| - | |||
Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos | Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos | ||
| - | conjuntos da el | + | conjuntos da el suceso imposible (conjunto vacío), decimos que ambos sucesos son complementarios o |
contrarios. | contrarios. | ||
| + | |||
| + | <br/> | ||
Para un suceso cualquiera | Para un suceso cualquiera | ||
| Línea 158: | Línea 174: | ||
A | A | ||
</math> | </math> | ||
| - | , y | + | , y viceversa. Se representa por |
<math> | <math> | ||
\overline{A} | \overline{A} | ||
| Línea 166: | Línea 182: | ||
<br/> | <br/> | ||
| - | En cualquier experimento aleatorio, todo suceso que se considere tiene su contrario. Las | + | En cualquier espacio muestral, obtenido de la realización de un experimento aleatorio, todo suceso que se considere tiene su contrario. Las |
| - | propiedades | + | propiedades más significativas de los sucesos contrarios son: |
<br/> | <br/> | ||
| Línea 180: | Línea 196: | ||
<br/> | <br/> | ||
| - | + | donde <math> | |
| + | E | ||
| + | </math> | ||
| + | representa el suceso seguro, compuesto por todos los sucesos elementales del espacio muestral. | ||
| + | |||
| + | <br/> | ||
==Algebra de Boole de sucesos== | ==Algebra de Boole de sucesos== | ||
| Línea 186: | Línea 207: | ||
<br/> | <br/> | ||
| - | La | + | La unión y la intersección de sucesos verifican las propiedades siguientes: conmutativa, asociativa, |
idempotente, simplificación, distributiva, existencia de elemento neutro y absorción: | idempotente, simplificación, distributiva, existencia de elemento neutro y absorción: | ||
Revisión actual
Tabla de contenidos |
Inclusión e igualdad de sucesos
Un suceso
está incluido (o contenido) en otro suceso
si todo suceso elemental perteneciente a
, pertenece también a
. Esta inclusión se representa por
.
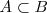Dos sucesos
y
son iguales si están formados por los mismos sucesos elementales. Ocurre que: 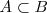y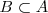 
. Se representa
por:
.
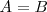Unión de sucesos
Si tenemos dos sucesos
y
de un mismo experimento aleatorio, llamamos suceso unión de
y
al suceso que se realiza cuando lo hacen
o
. Se representa por
.
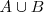Intersección de sucesos
Si tenemos dos sucesos
y
de un mismo experimento aleatorio, llamamos suceso intersección de
y
al suceso que se realiza cuando lo hacen
y
. Este suceso intersección está formado por todos los sucesos elementales que pertenecen a
y a
, al mismo tiempo. Se representa por
.
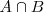Cuando
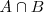es el suceso imposible, es decir, no hay ningún suceso elemental que pertenezca a A y a B al mismo tiempo, decimos que los sucesos
y
son incompatibles. Su intersección, como conjuntos, es igual al conjunto vacío.
(
)
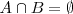En caso contrario, es decir, si la intersección es no vacía, decimos que
y
son compatibles.
Sucesos contrarios
Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos
conjuntos da el suceso imposible (conjunto vacío), decimos que ambos sucesos son complementarios o
contrarios.
Para un suceso cualquiera
de un experimento aleatorio, llamamos suceso contrario del suceso
al suceso que se verifica cuando no se verifica
, y viceversa. Se representa por
.
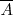En cualquier espacio muestral, obtenido de la realización de un experimento aleatorio, todo suceso que se considere tiene su contrario. Las propiedades más significativas de los sucesos contrarios son:
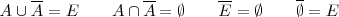
donde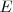 
representa el suceso seguro, compuesto por todos los sucesos elementales del espacio muestral.
Algebra de Boole de sucesos
La unión y la intersección de sucesos verifican las propiedades siguientes: conmutativa, asociativa, idempotente, simplificación, distributiva, existencia de elemento neutro y absorción:
