Curvas cónicas
De Wikillerato
(→Enlaces Externos) |
(→Enlaces Externos) |
||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
===Características generales=== | ===Características generales=== | ||
Las curvas cónicas son las secciones planas de un cono de revolución. | Las curvas cónicas son las secciones planas de un cono de revolución. | ||
| Línea 12: | Línea 10: | ||
===Elipses=== | ===Elipses=== | ||
| - | La elipse es la | + | La elipse es la curva que se obtiene al seccionar una superficie cónica mediante un plano oblicuo que corta a una sola rama. Es una curva cerrada y tiene dos ejes de simetría. Sus puntos cumplen todos ellos la propiedad de que sumadas sus distancias a otros dos puntos fijos, llamados focos y situados sobre su eje mayor, da una distancia constante e igual a la longitud de dicho eje. |
| - | + | ||
[[Imagen:36Curvasconicas.gif]] | [[Imagen:36Curvasconicas.gif]] | ||
| Línea 22: | Línea 19: | ||
===Hipérbolas=== | ===Hipérbolas=== | ||
| - | La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono. | + | La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono. Se llama hipérbola equilátera a la hipérbola cuyos semiejes son iguales. |
| - | + | ||
[[Imagen:38Curvasconicas.gif]] | [[Imagen:38Curvasconicas.gif]] | ||
| Línea 44: | Línea 40: | ||
:[http://trazoide.com/introduccion-8.html TRAZOIDE. Teoría y ejercicios resueltos sobre Dibujo Tecnico] | :[http://trazoide.com/introduccion-8.html TRAZOIDE. Teoría y ejercicios resueltos sobre Dibujo Tecnico] | ||
| - | + | {{problemas}}* [http://www.selectividad.tv/S_D_1_2_5_S_asintotas_de_una_hiperbola_definida_por_sus_focos_y_un_punto_p_de_la_misma.html Asintotas de una hipérbola definida por sus focos y un punto P de la misma] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_6_S_asintotas_de_una_hiperbola_definida_por_sus_focos_y_una_tangente_t.html Asíntotas de una hipérbola definida por sus focos y una tangente t] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_10_S_circunferencia_tangente_a_una_recta..html Circunferencia tangente a una recta] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_9_S_circunferencias_tangentes_comunes_a_una_recta_y_a_otra_circunferencia_conociendo_el_punto_de_tangencia_t.html Circunferencias tangentes comunes a una recta y a otra circunferencia, conociendo el punto de tangencia T] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_4_S_interseccion_de_una_recta_con_una_elipse.html Intersección de una recta con una elipse] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_3_S_interseccion_recta-parabola.html Intersección recta-parábola] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_1_S_parabola_definida_por_la_directriz_y_dos_rectas_tangentes.html Parábola definida por la directriz y dos rectas tangentes] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_8_S_parabola_definida_por_su_foco_una_tangente_y_el_eje..html Parábola definida por su foco, una tangente y el eje] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_7_S_parabola_definida_por_su_foco_una_tangente_y_el_punto_de_tangencia.html Parábola definida por su foco, una tangente y el punto de tangencia] | |
| - | + | * [http://www.selectividad.tv/S_D_1_2_11_S_rectas_tangentes_a_una_parabola_desde_un_punto_exterior_a_la_curva.html Rectas tangentes a una elipse desde un punto exterior a la curva] | |
| - | + | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión actual
Tabla de contenidos |
Características generales
Las curvas cónicas son las secciones planas de un cono de revolución.
Propiedades útiles en la resolución de problemas
1 - Si se une el simétrico de un foco respecto de una tangente con el punto de tangencia en esa recta esta el otro foco.
2 - La distancia desde el simétrico de un foco respecto de una tangente hasta el otro foco es el el mayor.
3 - La suma de las distancias desde un punto de la curva hasta los focos es igual al eje mayor.
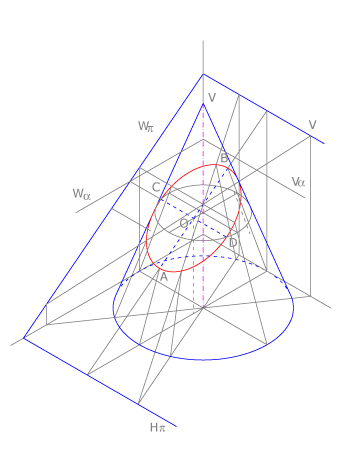
Elipses
La elipse es la curva que se obtiene al seccionar una superficie cónica mediante un plano oblicuo que corta a una sola rama. Es una curva cerrada y tiene dos ejes de simetría. Sus puntos cumplen todos ellos la propiedad de que sumadas sus distancias a otros dos puntos fijos, llamados focos y situados sobre su eje mayor, da una distancia constante e igual a la longitud de dicho eje.
Parábolas
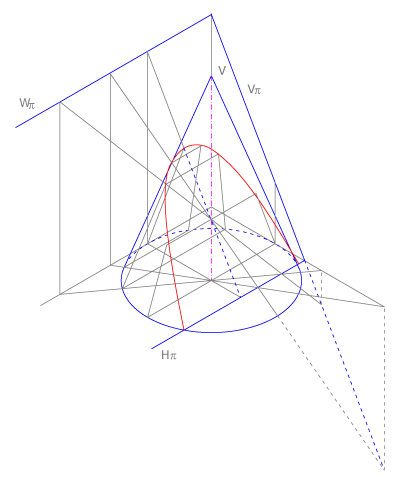
La parábola es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es paralelo a una de las generatrices.
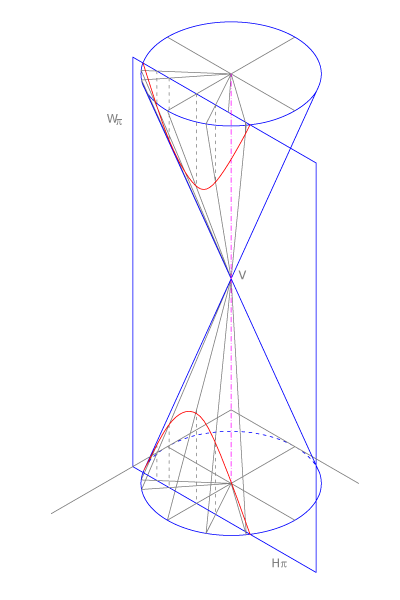
Hipérbolas
La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono. Se llama hipérbola equilátera a la hipérbola cuyos semiejes son iguales.
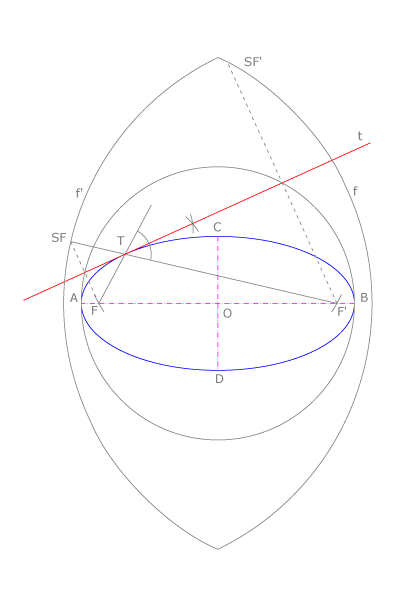
Rectas tangentes a las cónicas
La recta  tangente a una cónica en un punto
tangente a una cónica en un punto 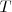 de la misma es bisectriz del ángulo
de la misma es bisectriz del ángulo 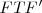 , siendo
, siendo  y
y 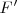 los focos de la curva. El punto
los focos de la curva. El punto 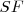 , simétrico del foco
, simétrico del foco  respecto
respecto  está sobre la circunferencia
está sobre la circunferencia 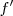 , focal de
, focal de 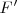 . Del mismo modo,
. Del mismo modo, 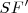 está sobre
está sobre 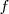 , focal de
, focal de  .
.
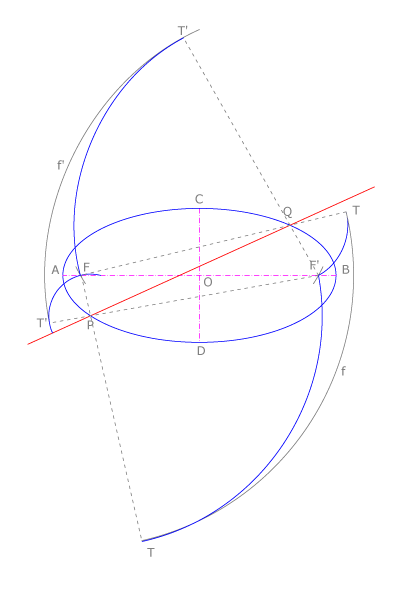
Intersecciones de rectas y cónicas
Los puntos  y
y 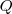 , intersección de la recta
, intersección de la recta  con una cónica, son los centros de las circunferencias que pasan por uno de los focos y son tangentes a la focal del otro foco.
En la figura vemos que
con una cónica, son los centros de las circunferencias que pasan por uno de los focos y son tangentes a la focal del otro foco.
En la figura vemos que  es centro de dos circunferencias: la que pasa por
es centro de dos circunferencias: la que pasa por  y es tangente en
y es tangente en 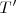 a la focal de
a la focal de 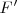 y la que pasa por
y la que pasa por 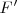 y es tangente en
y es tangente en 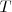 a la focal de
a la focal de  . Sucede otro tanto con
. Sucede otro tanto con 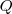 .
.
Enlaces Externos
- Problemas resueltos de todos los niveles
- TRAZOIDE. Teoría y ejercicios resueltos sobre Dibujo Tecnico
También te pueden interesar los siguientes ejercicios resueltos de selectividad
- Asintotas de una hipérbola definida por sus focos y un punto P de la misma
- Asíntotas de una hipérbola definida por sus focos y una tangente t
- Circunferencia tangente a una recta
- Circunferencias tangentes comunes a una recta y a otra circunferencia, conociendo el punto de tangencia T
- Intersección de una recta con una elipse
- Intersección recta-parábola
- Parábola definida por la directriz y dos rectas tangentes
- Parábola definida por su foco, una tangente y el eje
- Parábola definida por su foco, una tangente y el punto de tangencia
- Rectas tangentes a una elipse desde un punto exterior a la curva