Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Wikillerato:Portal de la comunidad

De Wikillerato

(Diferencias entre revisiones)
Revisión actual (17:10 25 feb 2014) (editar) (deshacer)
 
(22 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
__NOTOC__
__NOTOC__
-
Este portal de la comunidad es el lugar donde podéis expresar vuestras opiniones sobre este proyecto y crear grupos de discusión sobre diferentes temas relacionados con el mundo de la educación.
+
{{portal_destacado| Artículo destacado del mes| [[Métodos de integración]]|
 +
 
 +
No todos los '''métodos de integración''' son adecuados para todas las [[integrales]]. La
 +
habilidad de ver cuál es el método de integración mas idóneo para calcular una integral se
 +
adquiere resolviendo muchas integrales.
 +
 
 +
<br/>
 +
 
 +
==Integración por partes==
 +
 
 +
<br/>
 +
 
 +
La fórmula para la derivada de un producto es:
 +
<center>
 +
<math>
 +
\left( \, u \cdot v \, \right)^\prime = u^\prime \cdot v + u \cdot v^\prime
 +
</math>
 +
</center>
 +
Despejando el último sumando, queda:
 +
<center>
 +
<math>
 +
u \cdot v^\prime = \left( \, u \cdot v \, \right)^\prime - u^\prime \cdot v
 +
</math>
 +
</center>
 +
Si integramos en los dos miembros, se obtiene:
 +
<center>
 +
<math>
 +
\int u \cdot v^\prime \cdot \mathrm{d}x = \int \left( \, u \cdot v \, \right)^\prime \mathrm{d}x - \int
 +
u^\prime \cdot v \cdot\mathrm{d}x = u \cdot v - \int u^\prime \cdot v \cdot\mathrm{d}x
 +
</math>
 +
</center>
 +
La última igualdad es cierta porque una primitiva de la derivada de una función
 +
es esa misma función.
 +
 
 +
 
 +
[[Métodos de integración| (sigue leyendo...)]]
 +
}}
 +
 
 +
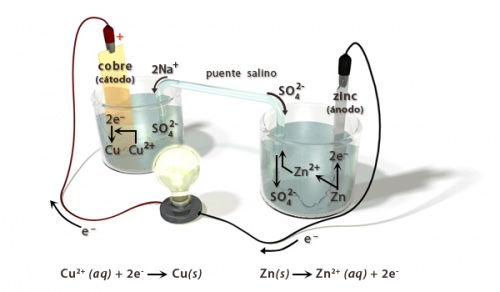
{{portal_destacado| Imagen destacada del mes| [[:Imagen:Pila-de-daniel-rotulada.jpg| Pila de Daniel]]|[[Imagen:Pila-de-daniel-rotulada.jpg|500px]]}}
 +
 
 +
<h2>Redes sociales</h2>
 +
 
 +
¡Síguenos en [http://www.twitter.com/wikillerato Twitter] y [http://www.facebook.com/pages/Wikillerato/185524501492896 Facebook] para mantenerte informado de las últimas novedades del proyecto!!
<h2>Participa</h2>
<h2>Participa</h2>
-
* Entra e intercambia mensajes con otros usuarios en la [[Wikillerato_Discusión:Portal_de_la_comunidad|página de discusión]] del portal.
+
* Entra e intercambia mensajes con otros usuarios en la [[Wikillerato_Discusión:Portal_de_la_comunidad|página de discusión]] del portal.
* Toma parte en las discusiones sobre [[:Categoría:Wikillerato:Consultas de borrado en curso| borrado de artículos]] y de [[Wikillerato:Votaciones para imágenes destacadas| votación de imágenes destacadas]].
* Toma parte en las discusiones sobre [[:Categoría:Wikillerato:Consultas de borrado en curso| borrado de artículos]] y de [[Wikillerato:Votaciones para imágenes destacadas| votación de imágenes destacadas]].
Línea 22: Línea 64:
* [[:Categoría:Wikillerato:Esbozos|Artículos que necesitan ser ampliados]]
* [[:Categoría:Wikillerato:Esbozos|Artículos que necesitan ser ampliados]]
* [[:Especial:Uncategorizedpages| Artículos que no tienen categoría]]
* [[:Especial:Uncategorizedpages| Artículos que no tienen categoría]]
-
 
-
 
-
{{portal_destacado| Artículo destacado| [[Método experimental de las ciencias empíricas]]|
 
-
Las '''ciencias empíricas, experimentales o naturales''' son aquellas que estudian los fenómenos observables en la naturaleza.
 
-
Se llaman experimentales porque parten de la experiencia y utilizan como criterio para aceptar sus tesis, la verificación experimental, su comprobación en la experiencia.
 
-
 
-
<b>Experiencia se define por tanto</b>, como todo objeto, hecho o fenómeno susceptible de ser observado o experimentado a través de la percepción sensible.[[Método experimental de las ciencias empíricas| (sigue leyendo...)]]
 
-
}}
 
-
 
-
{{portal_destacado| Imagen destacada| [[:Imagen:DibujoTecnico I-4 4.gif| Trazado general de un polígono regular a partir del radio]]|[[Imagen:DibujoTecnico I-4 4.gif]]}}
 

Revisión actual


Artículo destacado del mes

Métodos de integración


No todos los métodos de integración son adecuados para todas las integrales. La habilidad de ver cuál es el método de integración mas idóneo para calcular una integral se adquiere resolviendo muchas integrales.


Integración por partes


La fórmula para la derivada de un producto es:

\left( \, u \cdot v \, \right)^\prime = u^\prime \cdot v + u \cdot v^\prime

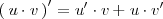
Despejando el último sumando, queda:

u \cdot v^\prime = \left( \, u \cdot v \, \right)^\prime - u^\prime \cdot v

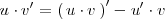
Si integramos en los dos miembros, se obtiene:

\int u \cdot v^\prime \cdot \mathrm{d}x = \int \left( \, u \cdot v \, \right)^\prime \mathrm{d}x - \int u^\prime \cdot v \cdot\mathrm{d}x = u \cdot v - \int u^\prime \cdot v \cdot\mathrm{d}x

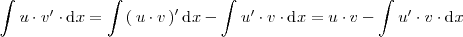
La última igualdad es cierta porque una primitiva de la derivada de una función es esa misma función.


(sigue leyendo...)


Imagen destacada del mes


Redes sociales

¡Síguenos en Twitter y Facebook para mantenerte informado de las últimas novedades del proyecto!!


Participa


Políticas, ayudas y recursos

¿Nuevo en Wikillerato? Antes de empezar a editar, conviene que eches un vistazo a los siguientes apartados:


¿Cómo colaborar?

Estas son algunas de las tareas pendientes en las que puedes ayudar:

Obtenido de "http://wikillerato.org/Wikillerato:Portal_de_la_comunidad.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.