Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

¿Qué es una matriz?

De Wikillerato

(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 190.3.246.67 (Talk); a la última edición de Laura.2mdc)
Revisión actual (11:22 16 oct 2012) (editar) (deshacer)
 
(57 ediciones intermedias no se muestran.)
Línea 5: Línea 5:
<br/>
<br/>
-
Una matriz es un cuadrado o tabla de números ordenados en filas y columnas. Se llama matriz de dimensión
+
Es una tabla bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse.
 +
 
 +
<br/>
 +
Una matriz es un cuadrado o tabla de números ordenados. Se llama matriz de dimensión
&nbsp;
&nbsp;
<math>
<math>
Línea 21: Línea 24:
<br/>
<br/>
 +
<center>
<center>
Línea 42: Línea 46:
La matriz &nbsp;
La matriz &nbsp;
<math>
<math>
-
A
+
\mathbf{A}
</math>
</math>
-
&nbsp; se puede denotar tambien como &nbsp;
+
&nbsp; se puede denotar también como &nbsp;
<math>
<math>
-
\quad A = \left( a_{ij} \right) \quad
+
\quad \mathbf{A} = \left( a_{ij} \right) \quad
</math>
</math>
&nbsp; donde
&nbsp; donde
Línea 70: Línea 74:
</math> designa un elemento generico de la matriz &nbsp;
</math> designa un elemento generico de la matriz &nbsp;
<math>
<math>
-
A
+
\mathbf{A}
</math>
</math>
, &nbsp; el elemento que se encuentra en la i-esima fila y j-esima columna.
, &nbsp; el elemento que se encuentra en la i-esima fila y j-esima columna.
-
 
<br/>
<br/>
-
El conjunto de matrices de dimension &nbsp;
+
==Tipos de matrices==
-
<math>
+
-
m \times n
+
-
</math>
+
-
&nbsp; se denota por:
+
<br/>
<br/>
-
<center>
+
===Matriz cuadrada===
-
<math>
+
-
M_{m \times n}
+
-
</math>
+
-
</center>
+
<br/>
<br/>
-
El conjunto de matrices de dimension &nbsp;
+
Las matrices cuadradas son aquellas que tienen el mismo número de filas que de
-
<math>
+
columnas.
-
n \times n
+
-
</math>
+
-
, &nbsp; tambien llamadas de orden &nbsp;
+
-
<math>
+
-
n
+
-
</math>
+
-
, &nbsp; se denota por:
+
<br/>
<br/>
-
<center>
+
En las matrices cuadradas tenemos:
-
<math>
+
-
M_n
+
-
</math>
+
-
</center>
+
<br/>
<br/>
-
Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
+
<span
-
 
+
style = 'color:#00aa00'>
-
* la diagonal principal formada por los elementos de la forma &nbsp;
+
&bull;
 +
</span>
 +
la diagonal principal formada por los elementos de la forma &nbsp;
<math>
<math>
a_{ii}
a_{ii}
Línea 120: Línea 106:
&nbsp;
&nbsp;
-
*la diagonal secundaria formada por los elementos de la forma &nbsp;
+
<span
 +
style = 'color:#00aa00'>
 +
&bull;
 +
</span>
 +
la diagonal secundaria formada por los elementos de la forma &nbsp;
<math>
<math>
a_{ij}
a_{ij}
Línea 137: Línea 127:
<br/>
<br/>
-
Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas que de columnas
+
===Matrices rectangulares===
-
&nbsp;
+
 
 +
<br/>
 +
 
 +
Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas
 +
que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular.
 +
 
 +
<br/>
 +
 
 +
====Ejemplo====
 +
 
 +
<br/>
 +
 
 +
<center>
<math>
<math>
-
\left(
+
\left(
-
m \neq n
+
\begin{array}[c]{ccc}
-
\right)
+
1 & -1 & ~~0
 +
\\
 +
2 & ~~3 & -1
 +
\end{array}
 +
\right)
 +
</math>
 +
</center>
 +
 
 +
<br/>
 +
 
 +
===Matrices filas===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz fila''''' es una matriz con una sola fila. Su dimensión es &nbsp;
 +
<math>
 +
1 \times n
</math>
</math>
.
.
 +
<br/>
-
====Ejemplo de matriz fila====
+
====Ejemplo====
<br/>
<br/>
Línea 163: Línea 182:
<br/>
<br/>
-
'''''Matriz columna''''' es toda matriz rectangular con una sola columna de dimension &nbsp;
+
===Matrices columna===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz columna''''' es una matriz rectangular con una sola columna. Su
 +
dimensión es &nbsp;
<math>
<math>
m \times 1
m \times 1
Línea 169: Línea 193:
.
.
-
====Ejemplo de matriz columna====
+
<br/>
 +
 
 +
====Ejemplo====
<br/>
<br/>
Línea 187: Línea 213:
<br/>
<br/>
-
Una '''''matriz nula''''' es una matriz rectangular con todos sus elementos nulos. Se denota
+
===Matrices nulas===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz nula''''' es una matriz cuyos elementos son todos nulos. Se denota
por &nbsp;
por &nbsp;
<math>
<math>
-
\mathbf{0}
+
\mathbf{0}_{m \times n}
</math>
</math>
.
.
-
====Ejemplo de matriz nula====
+
<br/>
 +
 
 +
Donde &nbsp;
 +
<math>
 +
m \times n
 +
</math>
 +
&nbsp; es la dimensión de la matriz.
 +
 
 +
<br/>
 +
 
 +
====Ejemplo====
<br/>
<br/>
Línea 212: Línea 252:
<br/>
<br/>
-
'''''Matriz triangular superior''''' es toda matriz cuadrada en la que todos los terminos
+
===Matrices triangulares superiores===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz triangular superior''''' es una matriz cuadrada en la que todos los terminos
situados por debajo de la diagonal principal son ceros.
situados por debajo de la diagonal principal son ceros.
-
====Ejemplo de matriz triangular superior====
+
<br/>
 +
 
 +
====Ejemplo====
<br/>
<br/>
Línea 235: Línea 281:
<br/>
<br/>
-
'''''Matriz triangular inferior''''' es toda matriz cuadrada en la que todos los terminos
+
===Matrices triangulares inferiores===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz triangular inferior''''' es una matriz cuadrada en la que todos los terminos
situados por encima de la diagonal principal son ceros.
situados por encima de la diagonal principal son ceros.
-
====Ejemplo de matriz triangular inferior====
+
<br/>
 +
 
 +
====Ejemplo ====
<br/>
<br/>
Línea 258: Línea 310:
<br/>
<br/>
-
'''''Matriz diagonal''''' es toda matriz cuadrada en la que todos los terminos
+
===Matrices diagonales===
-
no situados en la diagonal principal son ceros.
+
-
====Ejemplo de matriz diagonal====
+
<br/>
 +
 
 +
Una '''''matriz diagonal''''' es una matriz cuadrada en la que todos los terminos
 +
NO situados en la diagonal principal son ceros.
 +
 
 +
<br/>
 +
 
 +
====Ejemplo====
<br/>
<br/>
Línea 281: Línea 339:
<br/>
<br/>
-
'''''Matriz escalar''''' es toda matriz diagonal en la que todos los terminos
+
===Matrices escalares===
-
de la diagonal principal son iguales.
+
-
====Ejemplo de matriz escalar====
+
<br/>
 +
 
 +
Una '''''matriz escalar''''' es una matriz diagonal en la que todos los términos de la diagonal principal son iguales.
 +
 
 +
<br/>
 +
====Ejemplo====
<br/>
<br/>
Línea 305: Línea 367:
<br/>
<br/>
-
'''''Matriz unidad o identidad''''' es la matriz escalar cuyos elementos de la diagonal principal son
+
===Matrices unidad o identidad===
 +
 
 +
<br/>
 +
 
 +
Una '''''matriz unidad o identidad''''' es una matriz escalar cuyos elementos en la diagonal principal son
todos 1.
todos 1.
-
====Ejemplo de matriz unidad====
+
<br/>
 +
 
 +
====Ejemplo====
<br/>
<br/>
Línea 326: Línea 394:
</center>
</center>
-
 
+
<br/>
-
== Enlaces externos ==
+
-
# ''[http://www.matematicasypoesia.com.es/matematicas/VpMatricesSim.htm Matrices simétricas]'', J. A. Hervás. Matemáticas y Poesía.
+
-
# ''[http://www.matematicasypoesia.com.es/matematicas/MatBisimetricas.htm Matrices bisimétricas]'', J. A. Hervás. Matemáticas y Poesía.
+
-
 
+
[[Category:Matemáticas]]
[[Category:Matemáticas]]

Revisión actual

Tabla de contenidos


Definición de matriz


Es una tabla bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse.


Una matriz es un cuadrado o tabla de números ordenados. Se llama matriz de dimensión 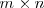  m \times n   a un conjunto de números reales dispuestos en 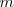  m   filas y   n   columnas de la siguiente forma  



\left( </p> <pre> \begin{array}[c]{cccc} a_{11 }& a_{12} & \ldots & a_{1n} \\ a_{21 }& a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1 }& a_{m2} & \ldots & a_{mn} \end{array} </pre> <p>\right)


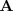La matriz   \mathbf{A}   se puede denotar también como 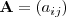  \quad \mathbf{A} = \left( a_{ij} \right) \quad   donde


\left\{ </p> <pre> \begin{array}[c]{l} i = 1, \, 2, \, \ldots, \, m \\ j = 1, \, 2, \, \ldots, \, n \end{array} </pre> <p>\right.


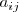a_{ij} designa un elemento generico de la matriz   \mathbf{A} ,   el elemento que se encuentra en la i-esima fila y j-esima columna.

Tipos de matrices


Matriz cuadrada


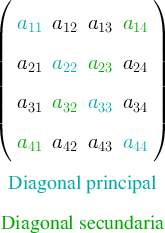
Las matrices cuadradas son aquellas que tienen el mismo número de filas que de columnas.


En las matrices cuadradas tenemos:


• la diagonal principal formada por los elementos de la forma   a_{ii}  

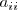
• la diagonal secundaria formada por los elementos de la forma 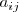  a_{ij}   tales que   i + j = n + 1


Image:diagonales.gif


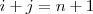
Matrices rectangulares


Una matriz rectangular es aquella que tiene distinto número de filas que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 1 & -1 & ~~0 \\ 2 & ~~3 & -1 \end{array} \right) </pre> <p>


Matrices filas


Una matriz fila es una matriz con una sola fila. Su dimensión es   1 \times n .


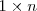Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} -1 & 3 & 5 \end{array} \right) </pre> <p>


Matrices columna


Una matriz columna es una matriz rectangular con una sola columna. Su dimensión es   m \times 1 .


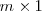Ejemplo


</p> <pre> \left( \begin{array}[c]{c} -1 \\ ~~3 \end{array} \right) </pre> <p>


Matrices nulas


Una matriz nula es una matriz cuyos elementos son todos nulos. Se denota por   \mathbf{0}_{m \times n} .


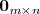Donde   m \times n   es la dimensión de la matriz.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right) </pre> <p>


Matrices triangulares superiores


Una matriz triangular superior es una matriz cuadrada en la que todos los terminos situados por debajo de la diagonal principal son ceros.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 1 & -1 & ~~0 \\ 0 & ~~3 & -1 \\ 0 & ~~0 & ~~2 \end{array} \right) </pre> <p>


Matrices triangulares inferiores


Una matriz triangular inferior es una matriz cuadrada en la que todos los terminos situados por encima de la diagonal principal son ceros.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 2 & ~~0 & 0 \\ 3 & -1 & 0 \\ 1 & -1 & 3 \end{array} \right) </pre> <p>


Matrices diagonales


Una matriz diagonal es una matriz cuadrada en la que todos los terminos NO situados en la diagonal principal son ceros.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} ~~2 & ~~0 & ~~0 \\ ~~0 & -1 & ~~0 \\ ~~0 & ~~0 & ~~3 \end{array} \right) </pre> <p>


Matrices escalares


Una matriz escalar es una matriz diagonal en la que todos los términos de la diagonal principal son iguales.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 2 & {0} & {0} \\ {0} & 2 & {0} \\ {0} & {0} & 2 \end{array} \right) </pre> <p>


Matrices unidad o identidad


Una matriz unidad o identidad es una matriz escalar cuyos elementos en la diagonal principal son todos 1.


Ejemplo


</p> <pre> \left( \begin{array}[c]{ccc} 1 & {0} & {0} \\ {0} & 1 & {0} \\ {0} & {0} & 1 \end{array} \right) </pre> <p>


Obtenido de "http://wikillerato.org/%C2%BFQu%C3%A9_es_una_matriz%3F.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.