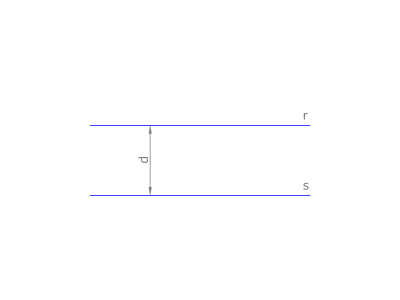Distancias
De Wikillerato
(→Hallar los puntos equidistantes una magnitud dada d de una recta y una circunferencia dadas.) |
(→Hallar el lugar geométrico de los puntos que equidisten de dos circunferencias de distinto radio.) |
||
| (4 ediciones intermedias no se muestran.) | |||
| Línea 27: | Línea 27: | ||
Vamos a considerar algunos casos fundamentales: | Vamos a considerar algunos casos fundamentales: | ||
| - | ====Hallar los puntos | + | ====Hallar los puntos que equidisten una magnitud dada '''d''' de una recta y una circunferencia dadas.==== |
| - | En este caso dibujamos el lugar geométrico de los puntos que | + | En este caso dibujamos el lugar geométrico de los puntos que se encuentran a una distancia '''d''' de la recta, que son dos rectas paralelas. Dibujamos el lugar geométrico de los puntos que estan a una distancia '''d''' de la circunferencia, que son las circunferencias concéntricas con ella de radios '''r+d''' y '''r-d'''. Las intersecciones de los lugares dibujados son los puntos '''P, Q, R, S, T, U''', soluciones del problema. |
[[Imagen:DibujoTecnico I-1 56.gif]] | [[Imagen:DibujoTecnico I-1 56.gif]] | ||
| Línea 35: | Línea 35: | ||
====Hallar los puntos que equidisten una magnitud dada '''d''' de una recta y una circunferencia dadas.==== | ====Hallar los puntos que equidisten una magnitud dada '''d''' de una recta y una circunferencia dadas.==== | ||
| - | Este es un caso igual al anterior, pero el radio del dato es menor que la distancia '''d'''. Se resuelve del mismo modo que el anterior. Es interesante hacer notar cómo | + | Este es un caso igual al anterior, pero el radio del dato es menor que la distancia '''d'''. Se resuelve del mismo modo que el anterior. Es interesante hacer notar cómo se mide la distancia desde el punto '''R''' (y desde el punto '''S'''). |
Las soluciones son los puntos '''P, Q, R, S.''' | Las soluciones son los puntos '''P, Q, R, S.''' | ||
| Línea 60: | Línea 60: | ||
====Hallar el lugar geométrico de los puntos que equidisten de dos circunferencias de distinto radio.==== | ====Hallar el lugar geométrico de los puntos que equidisten de dos circunferencias de distinto radio.==== | ||
| - | Se trazan circunferencias concéntricas a cada una de ellas equidistantes entre sí la misma magnitud. Se numeran. | + | Se trazan circunferencias concéntricas a cada una de ellas equidistantes entre sí, es decir con la misma magnitud. Se numeran. Finalmente las intersecciones de las concéntricas de igual número son puntos del lugar geométrico buscado. |
[[Imagen:DibujoTecnico I-1 60_thumb.gif]] | [[Imagen:DibujoTecnico I-1 60_thumb.gif]] | ||
Revisión actual
Definición
La distancia, en geometría siempre se entiende como la distancia mínima.
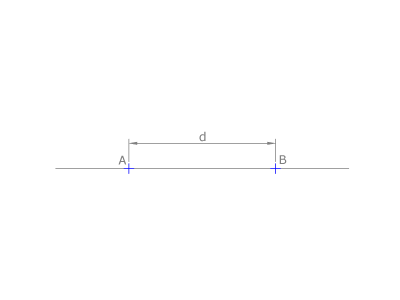
La distancia d entre dos puntos A y B es la magnitud del segmento definido por ellos.
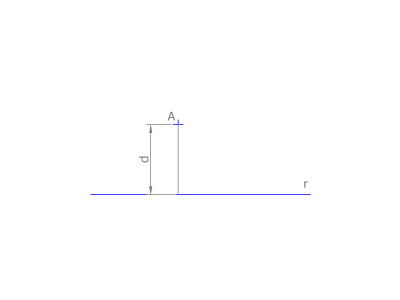
La distancia d entre un punto A y una recta r se mide sobre la perpendicular trazada desde A a r.
La distancia d entre dos rectas paralelas r y s se mide sobre una recta perpendicular común.
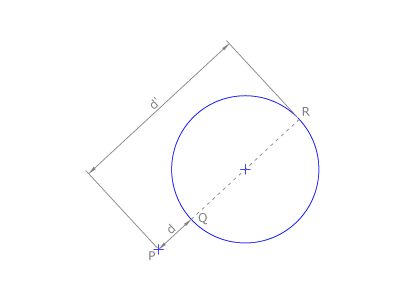
La distancia d de un punto P a una circunferencia se mide sobre la recta que une el punto con el centro de la circunferencia.
La distancia d entre dos circunferencias concéntricas se mide sobre un radio común a ambas.
Trazado de puntos equidistantes a rectas y circunferencias
Vamos a considerar algunos casos fundamentales:
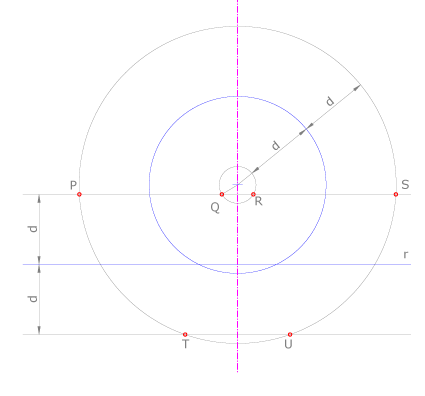
Hallar los puntos que equidisten una magnitud dada d de una recta y una circunferencia dadas.
En este caso dibujamos el lugar geométrico de los puntos que se encuentran a una distancia d de la recta, que son dos rectas paralelas. Dibujamos el lugar geométrico de los puntos que estan a una distancia d de la circunferencia, que son las circunferencias concéntricas con ella de radios r+d y r-d. Las intersecciones de los lugares dibujados son los puntos P, Q, R, S, T, U, soluciones del problema.
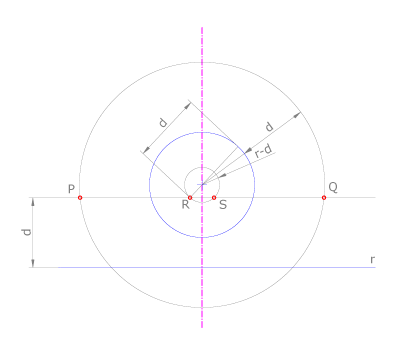
Hallar los puntos que equidisten una magnitud dada d de una recta y una circunferencia dadas.
Este es un caso igual al anterior, pero el radio del dato es menor que la distancia d. Se resuelve del mismo modo que el anterior. Es interesante hacer notar cómo se mide la distancia desde el punto R (y desde el punto S).
Las soluciones son los puntos P, Q, R, S.
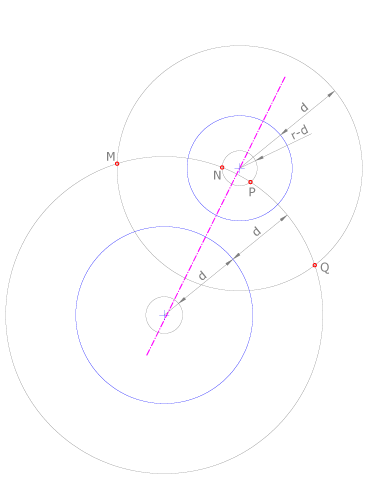
Hallar los puntos que equidisten una magnitud d de dos circunferencias dadas.
Se dibujan en cada caso los lugares geométricos, trazando circunferencias concéntricas de radios r+d y r-d.
Las intersecciones de dichos lugares son los puntos solución M, N, P, Q.
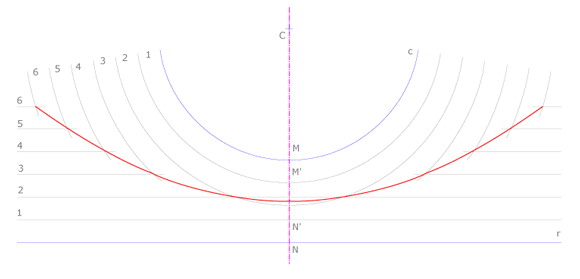
Dibujar el lugar geométrico de los puntos que equidisten de una circunferencia y una recta dadas.
Se dibuja un radio de la circunferencia que sea perpendicular a la recta y se prolonga, siendo M y N sus puntos de intersección con la circunferencia y la recta. El punto medio de MN pertenece al lugar buscado. Se trazan circunferencias concéntricas a la dada, equidistantes entre sí y se numeran. Se trazan paralelas a la recta dada equidistantes entre sí, de modo que la distancia entre las rectas sea igual a la distancia entre la paralelas. Se numeran. De este modo las intersecciones del arco y la recta de igual número pertenecerán al lugar buscado.
Unimos los puntos hallados y obtenemos un arco parabólico, que es el lugar geométrico solución del problema.
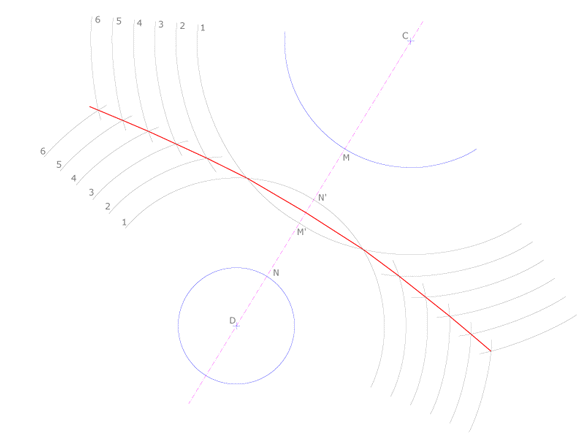
Hallar el lugar geométrico de los puntos que equidisten de dos circunferencias de distinto radio.
Se trazan circunferencias concéntricas a cada una de ellas equidistantes entre sí, es decir con la misma magnitud. Se numeran. Finalmente las intersecciones de las concéntricas de igual número son puntos del lugar geométrico buscado.