¿Qué es una matriz?

De Wikillerato

Revisión de 22:18 28 nov 2006 (editar) 83.61.34.7 (Discutir) (→Definición de matriz y tipos de matrices) ← Ir a diferencias anteriores		Revisión actual (11:22 16 oct 2012) (editar) (deshacer) Jvillalva (Discutir | contribuciones)
(106 ediciones intermedias no se muestran.)
Línea 1:		Línea 1:
-	Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension	+	__TOC__
		+
		+	==Definición de matriz==
		+
		+	<br/>
		+
		+	Es una tabla bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse.
		+
		+	<br/>
		+	Una matriz es un cuadrado o tabla de números ordenados. Se llama matriz de dimensión
	&nbsp;		&nbsp;
	<math>		<math>
Línea 15:		Línea 24:
	<br/>		<br/>
		+
	<center>		<center>
Línea 36:		Línea 46:
	La matriz &nbsp;		La matriz &nbsp;
	<math>		<math>
-	A	+	\mathbf{A}
	</math>		</math>
-	&nbsp; se puede designar tambien como &nbsp;	+	&nbsp; se puede denotar también como &nbsp;
	<math>		<math>
-	\quad A = \left( a_{ij} \right) \quad	+	\quad \mathbf{A} = \left( a_{ij} \right) \quad
	</math>		</math>
	&nbsp; donde		&nbsp; donde
Línea 60:		Línea 70:
	<br/>		<br/>
-	Un elemento generico de la matriz se designa por &nbsp;
	<math>		<math>
	a_{ij}		a_{ij}
-	</math>	+	</math> designa un elemento generico de la matriz &nbsp;
-	&nbsp; en el cual el subindice &nbsp;	+
	<math>		<math>
-	i	+	\mathbf{A}
	</math>		</math>
-	&nbsp; representa el numero de fila que ocupa el elemento y el subindice &nbsp;	+	, &nbsp; el elemento que se encuentra en la i-esima fila y j-esima columna.
-	<math>	+	<br/>
-	j	+
-	</math>	+
-	&nbsp; el numero de columna.	+
-	El conjunto de matrices de dimension &nbsp;	+	==Tipos de matrices==
-	<math>	+
-	m \times n	+
-	</math>	+
-	&nbsp; se denota por:	+
	<br/>		<br/>
-	<center>	+	===Matriz cuadrada===
-	<math>	+
-	M_{m \times n}	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	El conjunto de matrices de dimension &nbsp;	+	Las matrices cuadradas son aquellas que tienen el mismo número de filas que de
-	<math>	+	columnas.
-	n \times n	+
-	</math>	+
-	, &nbsp; tambien llamadas de orden &nbsp;	+
-	<math>	+
-	n	+
-	</math>	+
-	, &nbsp; se denota por:	+
	<br/>		<br/>
-	<center>	+	En las matrices cuadradas tenemos:
-	<math>	+
-	M_n	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:	+	<span
-		+	style = 'color:#00aa00'>
-	* la diagonal principal formada por los elementos de la forma &nbsp;	+	&bull;
		+	</span>
		+	la diagonal principal formada por los elementos de la forma &nbsp;
	<math>		<math>
	a_{ii}		a_{ii}
Línea 118:		Línea 106:
	&nbsp;		&nbsp;
-	*la diagonal secundaria formada por los elementos de la forma &nbsp;	+	<span
		+	style = 'color:#00aa00'>
		+	&bull;
		+	</span>
		+	la diagonal secundaria formada por los elementos de la forma &nbsp;
	<math>		<math>
	a_{ij}		a_{ij}
Línea 130:		Línea 122:
	<center>		<center>
-	<math>	+	[[Image:diagonales.gif]]
-	\begin{array}[c]{cc}	+
-	\left(	+
-	\begin{array}[c]{cccc}	+
-	\mathbf{a_{11}} & a_{12} & a_{13} & a_{14}	+
-	\\	+
-	a_{21} & \mathbf{a_{22}} & a_{23} & a_{24}	+
-	\\	+
-	a_{31} & a_{32} & \mathbf{a_{33}} & a_{34}	+
-	\\	+
-	a_{41} & a_{42} & a_{43} & \mathbf{a_{44}}	+
-	\end{array}	+
-	\right)	+
-	&	+
-	\left(	+
-	\begin{array}[c]{cccc}	+
-	a_{11} & a_{12} & a_{13} & \mathbf{a_{14}}	+
-	\\	+
-	a_{21} & a_{22} & \mathbf{a_{23}} & a_{24}	+
-	\\	+
-	a_{31} & \mathbf{a_{32}} & a_{33} & a_{34}	+
-	\\	+
-	\mathbf{a_{41}} & a_{42} & a_{43} & a_{44}	+
-	\end{array}	+
-	\right)	+
-	\\	+
-	&	+
-	\\	+
-	\makebox{Diagonal principal} & \makebox{Diagonal secundaria}	+
-	\end{array}	+
-	</math>	+
	</center>		</center>
	<br/>		<br/>
-	Una matriz rectangular es aquella que tiene distinto número de filas que de columnas	+	===Matrices rectangulares===
-	&nbsp;	+
-	<math>	+
-	\left(	+
-	m \neq n	+
-	\right)	+
-	</math>	+
-	Ejemplo:	+	<br/>
		+
		+	Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas
		+	que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular.
		+
		+	<br/>
		+
		+	====Ejemplo====
	<br/>		<br/>
Línea 191:		Línea 154:
	<br/>		<br/>
-	Matriz fila es toda matriz rectangular con una sola fila de dimension &nbsp;	+	===Matrices filas===
		+
		+	<br/>
		+
		+	Una '''''matriz fila''''' es una matriz con una sola fila. Su dimensión es &nbsp;
	<math>		<math>
	1 \times n		1 \times n
	</math>		</math>
-	Ejemplo:	+	.
		+
		+	<br/>
		+
		+	====Ejemplo====
	<br/>		<br/>
Línea 211:		Línea 182:
	<br/>		<br/>
-	Matriz columna es toda matriz rectangular con una sola columna de dimension &nbsp;	+	===Matrices columna===
		+
		+	<br/>
		+
		+	Una '''''matriz columna''''' es una matriz rectangular con una sola columna. Su
		+	dimensión es &nbsp;
	<math>		<math>
	m \times 1		m \times 1
	</math>		</math>
-	&nbsp;	+	.
-	Ejemplo:	+
		+	<br/>
		+
		+	====Ejemplo====
	<br/>		<br/>
Línea 234:		Línea 213:
	<br/>		<br/>
-	Una matriz nula es una matriz rectangular con todos sus elementos nulos. Se denota por	+	===Matrices nulas===
-	&nbsp;	+
		+	<br/>
		+
		+	Una '''''matriz nula''''' es una matriz cuyos elementos son todos nulos. Se denota
		+	por &nbsp;
	<math>		<math>
		+	\mathbf{0}_{m \times n}
	</math>		</math>
	.		.
-	Ejemplo:
	<br/>		<br/>
-	<center>	+	Donde &nbsp;
	<math>		<math>
-	\left(	+	m \times n
-	\begin{array}[c]{ccc}	+
-	0 & 0 & 0	+
-	\\	+
-	0 & 0 & 0	+
-	\end{array}	+
-	\right)	+
	</math>		</math>
-	</center>	+	&nbsp; es la dimensión de la matriz.
	<br/>		<br/>
-	Matriz triangular superior es toda matriz cuadrada en la que todos los terminos	+	====Ejemplo====
-	situados por debajo de la diagonal principal son ceros.	+
-	Ejemplo:	+
	<br/>		<br/>
Línea 268:		Línea 242:
	\left(		\left(
	\begin{array}[c]{ccc}		\begin{array}[c]{ccc}
-	1 & -1 & ~~0	+	0 & 0 & 0
	\\		\\
-	0 & ~~3 & -1	+	0 & 0 & 0
-	\\	+
-	0 & ~~0 & ~~2	+
	\end{array}		\end{array}
	\right)		\right)
Línea 280:		Línea 252:
	<br/>		<br/>
-	Matriz triangular inferior es toda matriz cuadrada en la que todos los terminos	+	===Matrices triangulares superiores===
-	situados por encima de la diagonal principal son ceros	+
-	Ejemplo:	+
	<br/>		<br/>
-	<center>	+	Una '''''matriz triangular superior''''' es una matriz cuadrada en la que todos los terminos
-	<math>	+	situados por debajo de la diagonal principal son ceros.
-	\left(	+
-	\begin{array}[c]{ccc}	+
-	2 & ~~0 & 0	+
-	\\	+
-	3 & -1 & 0	+
-	\\	+
-	1 & -1 & 3	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	Matriz diagonal es toda matriz cuadrada en la que todos los terminos	+	====Ejemplo====
-	no situados en la diagonal principal son ceros.	+
-	Ejemplo:	+
	<br/>		<br/>
Línea 312:		Línea 269:
	\left(		\left(
	\begin{array}[c]{ccc}		\begin{array}[c]{ccc}
-	~~2 & ~~0 & ~~0	+	1 & -1 & ~~0
	\\		\\
-	~~0 & -1 & ~~0	+	0 & ~~3 & -1
	\\		\\
-	~~0 & ~~0 & ~~3	+	0 & ~~0 & ~~2
	\end{array}		\end{array}
	\right)		\right)
Línea 324:		Línea 281:
	<br/>		<br/>
-	Matriz escalar es toda matriz diagonal en la que todos los terminos	+	===Matrices triangulares inferiores===
-	de la diagonal principal son iguales.	+
-	Ejemplo:	+
	<br/>		<br/>
-	<center>	+	Una '''''matriz triangular inferior''''' es una matriz cuadrada en la que todos los terminos
-	<math>	+	situados por encima de la diagonal principal son ceros.
-	\left(	+
-	\begin{array}[c]{ccc}	+
-	2 & {0} & {0}	+
-	\\	+
-	{0} & 2 & {0}	+
-	\\	+
-	{0} & {0} & 2	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	Matriz unidad es la matriz escalar cuyos elementos de la diagonal principal son todos	+	====Ejemplo ====
-	&nbsp;	+
-	<math>	+
-	1	+
-	</math>	+
-	&nbsp; .	+
-	Ejemplo:	+
	<br/>		<br/>
Línea 360:		Línea 298:
	\left(		\left(
	\begin{array}[c]{ccc}		\begin{array}[c]{ccc}
-	1 & {0} & {0}	+	2 & ~~0 & 0
	\\		\\
-	{0} & 1 & {0}	+	3 & -1 & 0
	\\		\\
-	{0} & {0} & 1	+	1 & -1 & 3
	\end{array}		\end{array}
	\right)		\right)
Línea 372:		Línea 310:
	<br/>		<br/>
-	==Producto de matrices==	+	===Matrices diagonales===
	<br/>		<br/>
-	El producto de dos matrices &nbsp;	+	Una '''''matriz diagonal''''' es una matriz cuadrada en la que todos los terminos
-	<math>	+	NO situados en la diagonal principal son ceros.
-	A = \left( a_{ij} \right)	+
-	</math>	+
-	&nbsp; de dimension &nbsp;	+
-	<math>	+
-	m \times n	+
-	</math>	+
-	&nbsp; y &nbsp;	+
-	<math>	+
-	B = \left( b_{ij} \right)	+
-	</math>	+
-	&nbsp; de dimension &nbsp;	+
-	<math>	+
-	n \times p	+
-	</math>	+
-	, &nbsp; es la matriz &nbsp;	+
-	<math>	+
-	A \cdot B	+
-	</math>	+
-	&nbsp; dada por:	+
	<br/>		<br/>
-	<center>	+	====Ejemplo====
-	<math>	+
-	A \cdot B = \left( c_{ij} \right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	con	+
	<br/>		<br/>
Línea 414:		Línea 325:
	<center>		<center>
	<math>		<math>
-	c_{ij} = \sum_{j = 1}^n a_{ij} \cdot b_{jk}	+	\left(
		+	\begin{array}[c]{ccc}
		+	~~2 & ~~0 & ~~0
		+	\\
		+	~~0 & -1 & ~~0
		+	\\
		+	~~0 & ~~0 & ~~3
		+	\end{array}
		+	\right)
	</math>		</math>
	</center>		</center>
Línea 420:		Línea 339:
	<br/>		<br/>
-	Es decir, cada elemento &nbsp;	+	===Matrices escalares===
-	<math>	+
-	c_{ik}	+
-	</math>	+
-	&nbsp; se obtiene multiplicando la fila i-ésima de la primera matriz por la columna	+
-	k-ésima de la segunda matriz.	+
-	Ejemplo:	+
	<br/>		<br/>
-	<center>	+	Una '''''matriz escalar''''' es una matriz diagonal en la que todos los términos de la diagonal principal son iguales.
-	<math>	+
-	\left(	+
-	\begin{array}[c]{ccc}	+
-	1 & 2 & 3	+
-	\\	+
-	4 & 5 & 6	+
-	\end{array}	+
-	\right)	+
-	\cdot	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	~~7 & ~~8	+
-	\\	+
-	~~9 & ~~0	+
-	\\	+
-	-1 & -2	+
-	\end{array}	+
-	\right)	+
-	=	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)	+
-	\\	+
-	4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	===Propiedades:===	+	====Ejemplo====
-		+
-	<br/>	+
-		+
-	*El producto de matrices cuadradas es asociativo:	+
	<br/>		<br/>
Línea 472:		Línea 353:
	<center>		<center>
	<math>		<math>
-	A \cdot	+	\left(
-	\left(	+	\begin{array}[c]{ccc}
-	B \cdot C	+	2 & {0} & {0}
-	\right)	+	\\
-	=	+	{0} & 2 & {0}
-	\left(	+	\\
-	A \cdot B	+	{0} & {0} & 2
-	\right)	+	\end{array}
-	\cdot C	+	\right)
	</math>		</math>
	</center>		</center>
Línea 486:		Línea 367:
	<br/>		<br/>
-	*El producto de matrices cuadradas de orden &nbsp;	+	===Matrices unidad o identidad===
-	<math>	+
-	n	+
-	</math>	+
-	&nbsp; posee como elemento neutro la matriz unidad o identidad &nbsp;	+
-	<math>	+
-	I	+
-	</math>	+
-	&nbsp; de orden &nbsp;	+
-	<math>	+
-	n	+
-	</math>	+
-	&nbsp; ya que:	+
	<br/>		<br/>
-	<center>	+	Una '''''matriz unidad o identidad''''' es una matriz escalar cuyos elementos en la diagonal principal son
-	<math>	+	todos 1.
-	A \cdot I = I \cdot A = A	+
-	</math>	+
-	</center>	+
	<br/>		<br/>
-	* El producto de matrices cuadradas es distributivo respecto de la suma de matrices:	+	====Ejemplo====
	<br/>		<br/>
Línea 516:		Línea 382:
	<center>		<center>
	<math>		<math>
-	A \cdot	+	\left(
-	\left(	+	\begin{array}[c]{ccc}
-	B + C	+	1 & {0} & {0}
-	\right)	+	\\
-	= A \cdot B + A \cdot C	+	{0} & 1 & {0}
		+	\\
		+	{0} & {0} & 1
		+	\end{array}
		+	\right)
	</math>		</math>
	</center>		</center>
Línea 526:		Línea 396:
	<br/>		<br/>
-	==Transposicion de matrices. Matriz simetrica y antisimetrica==	+	[[Category:Matemáticas]]
-		+
-	<br/>	+
-		+
-	Se llama matriz traspuesta de una matriz &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; de dimension &nbsp;	+
-	<math>	+
-	m \times n	+
-	</math>	+
-	, &nbsp; a la matriz que se obtiene al cambiar en &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; las filas por columnas o las columnas por filas. Se representa por &nbsp;	+
-	<math>	+
-	A^t	+
-	</math>	+
-	&nbsp; y su dimension es &nbsp;	+
-	<math>	+
-	n \times m	+
-	</math>	+
-		+
-	<br/>	+
-		+
-	===Propiedades:===	+
-		+
-	<br/>	+
-		+
-	* <math>	+
-	\left( \, A^t \, \right)^t = A	+
-	</math>	+
-		+
-	* <math>	+
-	\left( \, A + B \, \right)^t = A^t + B^t	+
-	</math>	+
-	&nbsp;	+
-		+
-	* <math>	+
-	\left( \, k \cdot A \, \right)^t = k \cdot A^t	+
-	</math>	+
-	&nbsp;	+
-		+
-	* <math>	+
-	\left( \, A \cdot B \, \right)^t = B^t \cdot A^t	+
-	</math>	+
-	&nbsp;	+
-		+
-	<br/>	+
-		+
-	Se llama matriz simetrica a toda matriz cuadrada &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; que coincide con su transpuesta: &nbsp;	+
-	<math>	+
-	A = A^t	+
-	</math>.	+
-	&nbsp; En una matriz simetrica cualquier par de elementos simetricos respecto a la	+
-	diagonal principal son iguales.	+
-	Ejemplo:	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\left(	+
-	\begin{array}[c]{ccc}	+
-	1 & 2 & 3	+
-	\\	+
-	2 & 4 & 5	+
-	\\	+
-	3 & 5 & 7	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	Se llama matriz antisimetrica a toda matriz cuadrada &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; que coincide con la opuesta de su transpuesta: &nbsp;	+
-	<math>	+
-	A = -A^t	+
-	</math>.	+
-	&nbsp; En una matriz simetrica cualquier par de elementos simetricos respecto a la	+
-	diagonal principal son opuestos.	+
-	Ejemplo:	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\left(	+
-	\begin{array}[c]{ccc}	+
-	~~ 0 & ~~2 & -3	+
-	\\	+
-	-2 & ~~0 & ~~5	+
-	\\	+
-	~~ 3 & -5 & ~~0	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	==Matriz inversa==	+
-		+
-	<br/>	+
-		+
-	La matriz inversa de una matriz cuadrada &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; de orden &nbsp;	+
-	<math>	+
-	n,	+
-	</math>	+
-	&nbsp; es la matriz &nbsp;	+
-	<math>	+
-	, A^{-1},	+
-	</math>	+
-	&nbsp; de orden &nbsp;	+
-	<math>	+
-	n	+
-	</math>	+
-	&nbsp; que verifica:	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	A \cdot A^{-1} = A^{-1} \cdot A = I	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices	+
-	singulares.	+
-		+
-	<br/>	+
-		+
-	===Calculo de la matriz inversa===	+
-		+
-	<br/>	+
-		+
-	Para calcular la matriz inversa de una matriz regular podemos utilizar dos	+
-	procedimientos:	+
-		+
-	<br/>	+
-		+
-	====Mediante la definicion====	+
-		+
-	<br/>	+
-		+
-	Por ejemplo para hallar la matriz inversa de la matriz	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	A =	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	1 & 2	+
-	\\	+
-	3 & 7	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	hacemos	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	A^{-1} =	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	a & b	+
-	\\	+
-	c & d	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	como	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	I = A \cdot A^{-1} \Rightarrow	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	1 & 2	+
-	\\	+
-	3 & 7	+
-	\end{array}	+
-	\right)	+
-	\cdot	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	a & b	+
-	\\	+
-	c & d	+
-	\end{array}	+
-	\right)	+
-	=	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	1 & 0	+
-	\\	+
-	0 & 1	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	Operando:	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	a + 2c & b + 2d	+
-	\\	+
-	3a + 7c & 3b + 7d	+
-	\end{array}	+
-	\right)	+
-	=	+
-	\left(	+
-	\begin{array}[c]{cc}	+
-	1 & 0	+
-	\\	+
-	0 & 1	+
-	\end{array}	+
-	\right)	+
-	\Leftrightarrow	+
-	\left\{	+
-	\begin{array}[c]{ccc}	+
-	a + 2c & = & 1	+
-	\\	+
-	3a + 7c & = & 0	+
-	\\	+
-	b + 2d & = & 0	+
-	\\	+
-	3b + 7d & = & 1	+
-	\\	+
-	\end{array}	+
-	\right.	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\Rightarrow \left\{	+
-	\begin{array}[c]{ccc}	+
-	a & = & 7	+
-	\\	+
-	b & = & -2	+
-	\\	+
-	c & = & -3	+
-	\\	+
-	d & = & 1	+
-	\\	+
-	\end{array}	+
-	\right.	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	====Método de Gauss-Jordan====	+
-		+
-	<br/>	+
-		+
-	La inversa de una matriz regular &nbsp;	+
-	<math>	+
-	A	+
-	</math>	+
-	&nbsp; se calcular transformando la matriz &nbsp;	+
-	<math>	+
-	\left(	+
-	\, A \, \left| \, I \, \right.	+
-	\right)	+
-	</math>	+
-	&nbsp; mediante operaciones elementales por filas en la matriz &nbsp;	+
-	<math>	+
-	\left(	+
-	\, I \, \left| \, A^{-1} \, \right.	+
-	\right)	+
-	</math>	+
-		+
-	Las operaciones elementales por filas en una matriz son las siguientes:	+
-		+
-	# Intercambiar las filas &nbsp;	+
-	<math>	+
-	i	+
-	</math>	+
-	&nbsp; y &nbsp;	+
-	<math>	+
-	j,	+
-	</math>	+
-	&nbsp; que designaremos por &nbsp;	+
-	<math>	+
-	F_i \longrightarrow F_j	+
-	</math>	+
-	&nbsp;	+
-		+
-	# Multiplicar la fila &nbsp;	+
-	<math>	+
-	i	+
-	</math>	+
-	&nbsp; por el numero &nbsp;	+
-	<math>	+
-	k \neq 0	+
-	</math>	+
-	&nbsp; y sustituirla por el resultado; lo designamos por &nbsp;	+
-	<math>	+
-	F_i \tau k \cdot F_i	+
-	</math>	+
-		+
-	# Multiplicar la fila &nbsp;	+
-	<math>	+
-	i	+
-	</math>	+
-	&nbsp; por el numero &nbsp;	+
-	<math>	+
-	k \neq 0	+
-	</math>	+
-	&nbsp; y sustituirla por el resultado; lo designamos por &nbsp;	+
-	<math>	+
-	F_i \tau k \cdot F_i	+
-	</math>	+
-		+
-	# Sumar las filas &nbsp;	+
-	<math>	+
-	i	+
-	</math>	+
-	&nbsp; y &nbsp;	+
-	<math>	+
-	j,	+
-	</math>	+
-	&nbsp;, multiplicadas por sendos números, y llevar el resultado a la fila &nbsp;	+
-	<math>	+
-	i	+
-	</math>	+
-	&nbsp; o &nbsp;	+
-	<math>	+
-	j	+
-	</math>	+
-	&nbsp;. Lo designamos por &nbsp;	+
-	<math>	+
-	F_i	+
-	</math>	+
-	&nbsp; o &nbsp;	+
-	<math>	+
-	F_j \to k \cdot F_i + t \cdot F_j	+
-	</math>	+
-		+
-	<br/>	+
-		+
-	==Rango de una matriz==	+
-		+
-	<br/>	+
-		+
-	En la matriz	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\left(	+
-	\begin{array}[c]{cccc}	+
-	a_{11 }& a_{12} & \ldots & a_{1n}	+
-	\\	+
-	a_{21 }& a_{22} & \ldots & a_{2n}	+
-	\\	+
-	\vdots & \vdots & \ddots & \vdots	+
-	\\	+
-	a_{m1 }& a_{m2} & \ldots & a_{mn}	+
-	\end{array}	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	Se dice que las filas &nbsp;	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	F_i, \, F_j, \, F_k, \, \ldots, \, F_t	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	\left(	+
-	\, F_i =	+
-	\left(	+
-	\, a_{i1 }, \, a_{i2}, \, \ldots, \, a_{in} \,	+
-	\right)	+
-	\right)	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	son dependientes si existen números &nbsp;	+
-	<math>	+
-	\alpha_j, \, \alpha_k, \, \ldots, \, \alpha_t \in R	+
-	</math>	+
-	&nbsp; tales que	+
-		+
-	<br/>	+
-		+
-	<center>	+
-	<math>	+
-	F_i = \alpha_j \cdot F_j + \alpha_k \cdot F_k + \, \ldots \, + \alpha_t \cdot F_t	+
-	</math>	+
-	</center>	+
-		+
-	<br/>	+
-		+
-	En caso contrario, se dice que las filas &nbsp;	+
-	<math>	+
-	F_i, \, F_j, \, F_k, \, \ldots, \, F_t	+
-	</math>	+
-	&nbsp; son linealmente independientes.	+
-		+
-	El '''rango''' de una matriz es el número de filas o de columnas linealmente independientes	+
-	que tiene esa matriz.	+

---

Revisión actual

Tabla de contenidos 1 Definición de matriz 2 Tipos de matrices 2.1 Matriz cuadrada 2.2 Matrices rectangulares 2.2.1 Ejemplo 2.3 Matrices filas 2.3.1 Ejemplo 2.4 Matrices columna 2.4.1 Ejemplo 2.5 Matrices nulas 2.5.1 Ejemplo 2.6 Matrices triangulares superiores 2.6.1 Ejemplo 2.7 Matrices triangulares inferiores 2.7.1 Ejemplo 2.8 Matrices diagonales 2.8.1 Ejemplo 2.9 Matrices escalares 2.9.1 Ejemplo 2.10 Matrices unidad o identidad 2.10.1 Ejemplo

Definición de matriz

Es una tabla bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse.

Una matriz es un cuadrado o tabla de números ordenados. Se llama matriz de dimensión 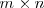    a un conjunto de números reales dispuestos en 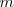    filas y     columnas de la siguiente forma  

La matriz 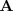    se puede denotar también como 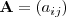    donde

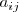designa un elemento generico de la matriz   ,   el elemento que se encuentra en la i-esima fila y j-esima columna.

Tipos de matrices

Matriz cuadrada

Las matrices cuadradas son aquellas que tienen el mismo número de filas que de columnas.

En las matrices cuadradas tenemos:

• la diagonal principal formada por los elementos de la forma    

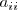
• la diagonal secundaria formada por los elementos de la forma 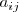    tales que  

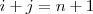
Matrices rectangulares

Una matriz rectangular es aquella que tiene distinto número de filas que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular.

Ejemplo

Matrices filas

Una matriz fila es una matriz con una sola fila. Su dimensión es   .

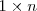Ejemplo

Matrices columna

Una matriz columna es una matriz rectangular con una sola columna. Su dimensión es   .

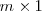Ejemplo

Matrices nulas

Una matriz nula es una matriz cuyos elementos son todos nulos. Se denota por   .

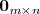Donde     es la dimensión de la matriz.

Ejemplo

Matrices triangulares superiores

Una matriz triangular superior es una matriz cuadrada en la que todos los terminos situados por debajo de la diagonal principal son ceros.

Ejemplo

Matrices triangulares inferiores

Una matriz triangular inferior es una matriz cuadrada en la que todos los terminos situados por encima de la diagonal principal son ceros.

Ejemplo

Matrices diagonales

Una matriz diagonal es una matriz cuadrada en la que todos los terminos NO situados en la diagonal principal son ceros.

Ejemplo

Matrices escalares

Una matriz escalar es una matriz diagonal en la que todos los términos de la diagonal principal son iguales.

Ejemplo

Matrices unidad o identidad

Una matriz unidad o identidad es una matriz escalar cuyos elementos en la diagonal principal son todos 1.

Ejemplo

   Tweet