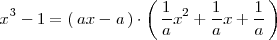La divisibilidad en los polinomios
De Wikillerato
m (Revertidas las ediciones realizadas por 190.80.212.141 (Talk); a la última edición de Laura.2mdc) |
|||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | <br/> | ||
| + | |||
==Definición de polinomio DIVISIBLE por otro== | ==Definición de polinomio DIVISIBLE por otro== | ||
| Línea 70: | Línea 72: | ||
x - 2 | x - 2 | ||
</math> | </math> | ||
| - | son divisores del polinomio | + | son divisores del polinomio |
| | ||
<math> | <math> | ||
| Línea 88: | Línea 90: | ||
de grado | de grado | ||
<math> | <math> | ||
| - | n | + | n > 0 |
</math> | </math> | ||
se dice que es irreducible cuando ningún polinomio de grado | se dice que es irreducible cuando ningún polinomio de grado | ||
| Línea 106: | Línea 108: | ||
<br/> | <br/> | ||
| - | + | ===Ejemplos=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ===Ejemplos | + | |
<br/> | <br/> | ||
| Línea 129: | Línea 126: | ||
<br/> | <br/> | ||
| - | == | + | <br/> |
| + | |||
| + | ==Factorización de polinomios== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Por '''''factorización de un polinomio''''' se entiende su descomposición en | ||
| + | forma de producto de polinomios irreducibles. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
<br/> | <br/> | ||
| Línea 169: | Línea 177: | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Tabla de contenidos |
Definición de polinomio DIVISIBLE por otro
Un polinomio
 es divisible por otro polinomio
es divisible por otro polinomio
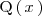 cuando existe otro polinomio
cuando existe otro polinomio
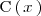 tal que
tal que
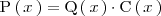
Los polinomios
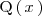 y
y
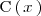 se llaman divisores de
se llaman divisores de
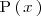 .
.
Ejemplo
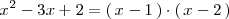
Por lo tanto, el polinomio
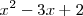 es divisible por los polinomios
es divisible por los polinomios
 y
y
 ,
o dicho de otra manera, los polinomios
,
o dicho de otra manera, los polinomios
 y
y
 son divisores del polinomio
son divisores del polinomio
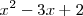 .
.
Definición de polinomio IRREDUCIBLE
Un polinomio
 de grado
de grado
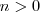 se dice que es irreducible cuando ningún polinomio de grado
menor que
se dice que es irreducible cuando ningún polinomio de grado
menor que
 y mayor que 0 es divisor de
y mayor que 0 es divisor de
 .
.
Cualquier polinomio que no sea irreducible se puede descomponer en forma de producto de polinomios irreducibles.
Ejemplos
Los siguientes dos polinomios son irreducibles:
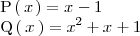
Factorización de polinomios
Por factorización de un polinomio se entiende su descomposición en forma de producto de polinomios irreducibles.
Ejemplo
Una descomposición del polinomio
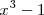 en producto de polinomios irreducibles es
en producto de polinomios irreducibles es
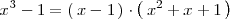
Otra posible descomposición del polinomio
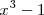 en producto de polinomios irreducibles es
en producto de polinomios irreducibles es
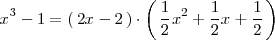
De hecho, hay infinitas descomposiciones posibles. Para cualquier número real
 distinto de 0, se tiene que
distinto de 0, se tiene que