Cálculo del rango de una matriz por menores
De Wikillerato
m (Revertidas las ediciones realizadas por 190.29.162.161 (Talk); a la última edición de Fjmolina) |
|||
| (11 ediciones intermedias no se muestran.) | |||
| Línea 114: | Línea 114: | ||
<br/> | <br/> | ||
| - | Es decir, si el rango de una matriz es k, entonces todos los menores de orden superior a k son | + | Es decir, si el rango de una matriz es k, entonces todos los menores de orden |
| - | nulos. | + | superior a k, si los hubiese, son |
| + | nulos. O dicho de otra manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si todos los menores de orden k y de orden mayor que k de una matriz son nulos, entonces el | ||
| + | rango de dicha matriz tiene que ser menor que k. | ||
<br/> | <br/> | ||
| Línea 154: | Línea 160: | ||
</math>, | </math>, | ||
| | ||
| - | + | el que sea menor. | |
<br/> | <br/> | ||
| Línea 170: | Línea 176: | ||
k | k | ||
</math> | </math> | ||
| - | se | + | se va comprobando si algún menor de orden |
<math> | <math> | ||
k | k | ||
</math> | </math> | ||
| - | es cero | + | es cero. |
<br/> | <br/> | ||
| - | + | Considerando distintos valores de | |
<math> | <math> | ||
k | k | ||
</math> | </math> | ||
| - | en este orden, | + | en este orden, el primer valor de |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
k | k | ||
</math> | </math> | ||
| - | + | que encontramos con un menor NO nulo | |
| + | es el rango de | ||
<math> | <math> | ||
| - | + | \mathbf{A} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | \ | + | |
</math>. | </math>. | ||
<br/> | <br/> | ||
| - | Si no | + | Si no encontrasemos ningún |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
k | k | ||
</math> | </math> | ||
| - | de | + | satisfaciendo esta condición, entonces NO existiría ningún menor de |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | distinto de cero y el rango de | |
| - | + | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | seria cero. | |
<br/> | <br/> | ||
| Línea 287: | Línea 265: | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | son cero y por el [[ | + | son cero y por el [[Cálculo del rango de una matriz por menores#Teorema|teorema anterior]] el rango de |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
| Línea 295: | Línea 273: | ||
<br/> | <br/> | ||
| - | Como | + | Como todos los menores de orden 3 son nulos, pasamos a inspeccionar los menores de orden 3 - 1 = 2, y comprobamos |
si todos ellos son nulos ( cero ) o no. | si todos ellos son nulos ( cero ) o no. | ||
| Línea 318: | Línea 296: | ||
\mathbf{A} | \mathbf{A} | ||
</math>, | </math>, | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 2 & 4 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
<br/> | <br/> | ||
| Línea 329: | Línea 323: | ||
<br/> | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 2 & 3 | ||
| + | \\ | ||
| + | 4 & 6 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
#3. El tercer menor que calculamos es el que se obtiene seleccionando las ultimas dos | #3. El tercer menor que calculamos es el que se obtiene seleccionando las ultimas dos | ||
| Línea 336: | Línea 344: | ||
\mathbf{A} | \mathbf{A} | ||
</math>. | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 4 & 6 | ||
| + | \\ | ||
| + | 0 & 5 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | = 20 | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| Línea 346: | Línea 369: | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | tiene que ser mayor que 2. Como ya habiamos averiguado antes que el rango de | + | tiene que ser mayor o igual que 2. Como ya habiamos averiguado antes que el rango de |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
Revisión actual
Tabla de contenidos |
Definición de menor de una matriz
Se llama menor de orden k de una matriz
 al determinante de orden k que está formado por los elementos que pertenecen a k
filas y a k columnas de la matriz
al determinante de orden k que está formado por los elementos que pertenecen a k
filas y a k columnas de la matriz
 .
.
En este determinante los elementos de
 conservan las posiciones relativas que tienen en la matriz
conservan las posiciones relativas que tienen en la matriz
 .
.
Es decir, si la fila de
 en la que se encuentra
en la que se encuentra
 esta por encima de la fila de
esta por encima de la fila de
 en la que se encuentra
en la que se encuentra
 ,
entonces, en los menores de
,
entonces, en los menores de
 en los que aparezcan
en los que aparezcan
 y
y
 ,
la fila en la que se encuentra
,
la fila en la que se encuentra
 va a estar por encima de la fila en la que se encuentra
va a estar por encima de la fila en la que se encuentra
 .
.
Analogamente, si la columna de
 en la que se encuentra
en la que se encuentra
 esta a la derecha de la columna de
esta a la derecha de la columna de
 en la que se encuentra
en la que se encuentra
 ,
entonces, en los menores de
,
entonces, en los menores de
 en los que aparezcan
en los que aparezcan
 y
y
 ,
la columna en la que se encuentra
,
la columna en la que se encuentra
 va a estar a la derecha de la columna en la que se encuentra
va a estar a la derecha de la columna en la que se encuentra
 .
.
Teorema
El rango de una matriz es el orden del mayor menor no nulo que podemos obtener de esta matriz.
Es decir, si el rango de una matriz es k, entonces todos los menores de orden superior a k, si los hubiese, son nulos. O dicho de otra manera:
Si todos los menores de orden k y de orden mayor que k de una matriz son nulos, entonces el rango de dicha matriz tiene que ser menor que k.
Siendo esto así, el procedimiento que describimos a continuacion nos permite
calcular el rango de una matriz
 independientemente de como sea la matriz
independientemente de como sea la matriz
 .
.
Procedimiento para calcular el rango de una matriz usando menores
Sea
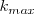 el orden de los menores de mayor orden de la matriz
el orden de los menores de mayor orden de la matriz
 .
.
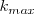 es el número de filas o el número de columnas de
es el número de filas o el número de columnas de
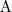 ,
el que sea menor.
,
el que sea menor.
Empezando por
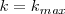 y continuando con
y continuando con
 ,
para cada valor de
,
para cada valor de
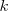 se va comprobando si algún menor de orden
se va comprobando si algún menor de orden
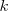 es cero.
es cero.
Considerando distintos valores de
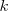 en este orden, el primer valor de
en este orden, el primer valor de
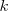 que encontramos con un menor NO nulo
es el rango de
que encontramos con un menor NO nulo
es el rango de
 .
.
Si no encontrasemos ningún
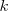 satisfaciendo esta condición, entonces NO existiría ningún menor de
satisfaciendo esta condición, entonces NO existiría ningún menor de
 distinto de cero y el rango de
distinto de cero y el rango de
 seria cero.
seria cero.
Ejemplo
Calculemos el determinante de la matriz
![\mathbf{A} =
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 6
\\
-1 & 0 & 5
\end{array}
</pre>
<p>\right)
\mathbf{A} =
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 6
\\
-1 & 0 & 5
\end{array}
</pre>
<p>\right)](/images/math/math-2637e92125a23689f50f71bd8176eed5.png)
En este caso
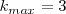 .
Comprobamos primero si todos los menores de orden
.
Comprobamos primero si todos los menores de orden
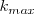 son nulos.
son nulos.
En este caso, solo hay un menor de orden 3,
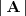 ,
por lo tanto, solo tenemos que
calcular un determinante de orden 3.
,
por lo tanto, solo tenemos que
calcular un determinante de orden 3.
Como, despues de hacer las cuentas, resulta que
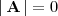 todos los menores de orden 3 de
todos los menores de orden 3 de
 son cero y por el teorema anterior el rango de
son cero y por el teorema anterior el rango de
 ha de ser menor que 3.
ha de ser menor que 3.
Como todos los menores de orden 3 son nulos, pasamos a inspeccionar los menores de orden 3 - 1 = 2, y comprobamos si todos ellos son nulos ( cero ) o no.
 tiene 9 menores de orden 2. Calculamos uno por uno para comprobar si alguno de
ellos es distinto de cero. Si encontramos que alguno de ellos es cero paramos.
tiene 9 menores de orden 2. Calculamos uno por uno para comprobar si alguno de
ellos es distinto de cero. Si encontramos que alguno de ellos es cero paramos.
Supongamos que empezamos a calcular estos 9 menores en el siguiente orden:
- 1. Primero calculamos el menor que se obtiene seleccionando las primeras dos
filas ( las de mas arriba ) y las primeras dos columnas ( las de mas a la
izquierda ) de
 ,
,
![\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
2 & 4
\end{array}
</pre>
<p>\right|
</p>
<pre>= 0
</pre>
<p>
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
2 & 4
\end{array}
</pre>
<p>\right|
</p>
<pre>= 0
</pre>
<p>](/images/math/math-0f0161550e1318f68bfedb2146605aba.png)
- 2. A continuación calculamos el menor que se obtiene seleccionando las primeras dos
filas ( las de mas arriba ) y las ultimas dos columnas ( las de mas a la
derecha ) de
 ,
,
![\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
</p>
<pre>= 0
</pre>
<p>
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
</p>
<pre>= 0
</pre>
<p>](/images/math/math-8ba2c3dfbc92cfc0d2265ad33a5a5dc6.png)
- 3. El tercer menor que calculamos es el que se obtiene seleccionando las ultimas dos
filas ( las de mas arriba ) y las ultimas dos columnas ( las de mas a la
derecha ) de
 .
.
![\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
0 & 5
\end{array}
</pre>
<p>\right|
</p>
<pre>= 20
</pre>
<p>
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
0 & 5
\end{array}
</pre>
<p>\right|
</p>
<pre>= 20
</pre>
<p>](/images/math/math-7f29dabab2ede314db03d5113fb48302.png)
Procediendo asi, hubiesemos obtenido que los dos primeros menores son cero, pero
como el tercer menor ya nos sale distinto de cero, paramos y concluimos que, como
un menor de orden 2
es distinto de cero, por el teorema anterior el rango de
 tiene que ser mayor o igual que 2. Como ya habiamos averiguado antes que el rango de
tiene que ser mayor o igual que 2. Como ya habiamos averiguado antes que el rango de
 tiene que ser menor que 3, deducimos que el rango de
tiene que ser menor que 3, deducimos que el rango de
 es 2.
es 2.



