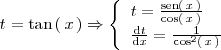Métodos de integración
De Wikillerato
(→Introducción) |
|||
| (69 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | ==Introducción== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | No todos los '''métodos de integración''' son adecuados para todas las [[Integral indefinida|integrales]]. La | ||
| + | habilidad de ver cuál es el método de integración más idóneo para calcular una integral se | ||
| + | adquiere resolviendo muchas integrales. | ||
| + | |||
| + | <br/> | ||
==Integración por partes== | ==Integración por partes== | ||
| Línea 89: | Línea 98: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \int u \cdot v^\prime \cdot \mathrm{d}x = | + | \int u \cdot v^\prime \cdot \mathrm{d}x = u \cdot v - \int |
u^\prime \cdot v \cdot\mathrm{d}x | u^\prime \cdot v \cdot\mathrm{d}x | ||
</math> | </math> | ||
| Línea 141: | Línea 150: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Despejando | Despejando | ||
| Línea 187: | Línea 189: | ||
<math> | <math> | ||
\int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| - | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g} \left( | + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( |
t \right) \cdot \mathrm{d}t | t \right) \cdot \mathrm{d}t | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | ||
| + | <br/> | ||
| + | |||
| + | Integrando obtenemos una primitiva | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{g} \left( x \right) |
</math> | </math> | ||
| - | | + | de |
| | ||
<math> | <math> | ||
| - | \mathrm{g} \left( x \right) | + | \mathrm{g}^\prime \left( x \right) |
| - | </math> | + | </math>. |
| - | + | ||
<center> | <center> | ||
<math> | <math> | ||
\int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| - | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g} \left( | + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( |
| - | t \right) \cdot \mathrm{d}t = \mathrm{ | + | t \right) \cdot \mathrm{d}t = \mathrm{g} \left( t \right) + C= \mathrm{g} \left( |
| - | \mathrm{f} \left( x \right)\right) + C | + | \, \mathrm{f} \left( x \right)\right) + C |
</math> | </math> | ||
</center> | </center> | ||
| - | Las igualdades anteriores resumen en que consiste el metodo de sustitución. | + | Las igualdades anteriores resumen en que consiste el metodo de sustitución. El |
| - | + | método de sustitución es util en tanto en cuanto sea relativamente facil encontrar una primitiva | |
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{g} |
</math> | </math> | ||
de | de | ||
<math> | <math> | ||
| - | \mathrm{g} | + | \mathrm{g}^\prime |
</math>. | </math>. | ||
| Línea 235: | Línea 240: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \begin{array}{ | + | \begin{array}{rl} |
| - | \mathrm{g} \left( x \right) & = \cos \left( x \right) | + | \mathrm{g}^\prime \left( x \right) & = \mathrm{cos} \left( x \right) |
\\ | \\ | ||
| - | \mathrm{f} \left( x \right) & = e^x | + | t = \mathrm{f} \left( x \right) & = e^x |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Línea 245: | Línea 250: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \begin{array}{ | + | \begin{array}{rcl} |
| - | \mathrm{f}^\prime \left( x \right) & = e^x | + | \mathrm{f}^\prime \left( x \right) & = & e^x \left( \, \Rightarrow \mathrm{d}t = |
| + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = e^x \cdot \mathrm{dx} \, \right) | ||
\\ | \\ | ||
| - | \int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x & = | + | \int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x & = & \int |
| - | \mathrm{g} \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x | + | \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Línea 255: | Línea 261: | ||
En este caso, una primitiva de | En este caso, una primitiva de | ||
<math> | <math> | ||
| - | \mathrm{g} \left( x \right) | + | \mathrm{g}^\prime \left( x \right) |
</math> | </math> | ||
es | es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{g} \left( \, x \, \right) = \mathrm{sen} \left( \, x \, \right) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 267: | Línea 273: | ||
<math> | <math> | ||
\int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| - | \mathrm{f}^\prime \left( x \right) | + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( |
| - | t \right) \cdot \mathrm{d}t = \mathrm{ | + | t \right) \cdot \mathrm{d}t = \mathrm{g} \left( t \right) + C= \mathrm{g} \left( |
\mathrm{f} \left( x \right)\right) + C = \mathrm{sen} \left( e^x \right) + C | \mathrm{f} \left( x \right)\right) + C = \mathrm{sen} \left( e^x \right) + C | ||
</math> | </math> | ||
</center> | </center> | ||
| + | <br/> | ||
| + | |||
| + | ==Integración de cocientes de polinomios== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Sean | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math> | ||
| + | dos polinomios, entonces: | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{P} \left( \, x \, \right)}{\mathrm{Q} \left( \, x \, \right)} = | ||
| + | \mathrm{C} \left( \, x \, \right) + \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{Q} \left( \, x \, \right)} | ||
| + | </math> | ||
| + | </center> | ||
| + | donde | ||
| + | <math> | ||
| + | \mathrm{C} \left( \, x \, \right) | ||
| + | </math> | ||
| + | es un polinomio ( el cociente ) y | ||
| + | <math> | ||
| + | \mathrm{R} \left( \, x \, \right) | ||
| + | </math> | ||
| + | es otro polinomio ( el resto ) de grado menor al grado de | ||
| + | | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si el grado de | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) | ||
| + | </math> | ||
| + | es menor que el grado de | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math>, | ||
| + | entonces | ||
| + | <math> | ||
| + | \mathrm{C} \left( \, x \, \right) | ||
| + | </math> | ||
| + | es cero y | ||
| + | <math> | ||
| + | \mathrm{R} \left( \, x \, \right) = \mathrm{P} \left( \, x \, \right) | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{\mathrm{P} \left( \, x \, \right)}{\mathrm{Q} \left( \, x \, | ||
| + | \right)} \cdot \mathrm{d}x = | ||
| + | \int \mathrm{C} \left( \, x \, \right) \cdot \mathrm{d}x + \int \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{Q} \left( \, x \, | ||
| + | \right)} \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | nos podemos restringir al caso en el que el grado del polinomio divisor, | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math>, | ||
| + | es mayor que grado del polinomio dividendo, | ||
| + | | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para resolver este tipo de integrales lo primero que hay que hacer es | ||
| + | [[La divisibilidad en los polinomios#Factorización de polinomios|factorizar]] | ||
| + | el polinomio divisor | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Al factorizar | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math> | ||
| + | lo podemos poner como un producto de polinomios de grado | ||
| + | uno y/o de grado dos: | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) = \left( \, x - r_1 \, \right)^{k_1} \cdot | ||
| + | \left( \, x - r_2 \, \right)^{k_2} \cdot \ldots \cdot \left( \, x - r_m \, \right)^{k_m} \cdot | ||
| + | \mathrm{Q}_1 \left( \, x \, \right) \cdot \mathrm{Q}_2 \left( \, x \, \right) | ||
| + | \cdot \ldots \cdot \mathrm{Q}_n \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | donde | ||
| + | <center> | ||
| + | <math> | ||
| + | r_1, \, r_2, \, \ldots, \, r_m | ||
| + | </math> | ||
| + | </center> | ||
| + | son todas las raices reales de | ||
| + | <math> | ||
| + | \mathrm{Q} \left( \, x \, \right) | ||
| + | </math> | ||
| + | y | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{Q}_1 \left( \, x \, \right), \, \mathrm{Q}_2 \left( \, x \, \right), \, | ||
| + | \ldots, \, \mathrm{Q}_n \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | son polinomios de grado dos irreducibles ( sin raices reales ). | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | De esta forma | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{P} \left( \, x \, \right)}{\mathrm{Q}\left( \, x \, \right)} = | ||
| + | \frac{A_{1,1}}{\left( \, x - r_1 \, \right)} \cdot \mathrm{d}x + | ||
| + | \frac{A_{1,2}}{\left( \, x - r_1 \, \right)^2} \cdot \mathrm{d}x + | ||
| + | \ldots + \frac{A_{1,k_1}}{\left( \, x - r_1 \, \right)^{k_1}} \cdot | ||
| + | \mathrm{d}x + | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | + \frac{A_{2,1}}{\left( \, x - r_2 \, \right)} \cdot \mathrm{d}x + | ||
| + | \frac{A_{2,2} \cdot x}{\left( \, x - r_2 \, \right)^2} \cdot \mathrm{d}x + | ||
| + | \ldots + \frac{A_{2,k_2}}{\left( \, x - r_2 \, \right)^{k_2}} \cdot | ||
| + | \mathrm{d}x + \ldots + | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | + \frac{A_{m,1}}{\left( \, x - r_m \, \right)} \cdot \mathrm{d}x + | ||
| + | \frac{A_{m,2} \cdot x}{\left( \, x - r_m \, \right)^2} \cdot \mathrm{d}x + | ||
| + | \ldots + \frac{A_{m,k_m}}{\left( \, x - r_m \, \right)^{k_m}} \cdot | ||
| + | \mathrm{d}x | ||
| + | + | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{B_1 \cdot x + C_1}{\mathrm{Q}_1 \left( \, x \, \right)} + | ||
| + | \frac{B_2 \cdot x + C_2}{\mathrm{Q}_2 \left( \, x \, \right)} + | ||
| + | \ldots | ||
| + | + | ||
| + | \frac{B_n \cdot x + C_n}{\mathrm{Q}_n \left( \, x \, \right)} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Donde hemos seguido la siguiente notación: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <span | ||
| + | style = 'color:#00aa00'> | ||
| + | 1 | ||
| + | </span>. | ||
| + | <math> | ||
| + | A_{i,j} | ||
| + | </math> | ||
| + | es la constante a la que divide | ||
| + | <math> | ||
| + | \left( \, x - r_i \, \right)^j | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <span | ||
| + | style = 'color:#00aa00'> | ||
| + | 2 | ||
| + | </span>. | ||
| + | <math> | ||
| + | B_i \cdot x + C_i | ||
| + | </math> | ||
| + | es el polinomio de grado uno al que divide | ||
| + | | ||
| + | <math> | ||
| + | \mathrm{Q}_i \left( \, x \, \right) | ||
| + | </math>. | ||
| + | | ||
| + | <math> | ||
| + | B_i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | C_i | ||
| + | </math> | ||
| + | son constantes ( números reales que no dependen de | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | ). | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Por lo tanto, la integral de | ||
| + | <math> | ||
| + | \frac{\mathrm{P}\left( \, x \, \right)}{\mathrm{Q} \left( \, x \, \right)} | ||
| + | </math> | ||
| + | es la suma de las integrales de las fracciones mas simples en las que | ||
| + | hemos descompuesto | ||
| + | <math> | ||
| + | \frac{\mathrm{P}\left( \, x \, \right)}{\mathrm{Q} \left( \, x \, \right)} | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Estas integrales mas simples son casi inmediatas. Así | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{A_{i,j}}{\left( \, x - r_i \, \right)^j} \cdot \mathrm{d}x = | ||
| + | \frac{A_{i,j}}{\left( \, 1 - j \, \right) \cdot \left( \, x - r_i \, | ||
| + | \right)^\left( \, j - 1 \, \right)} | ||
| + | </math> | ||
| + | </center> | ||
| + | Esta integral se puede resolver utilizando el cambio de variable | ||
| + | <math> | ||
| + | x - r_i \longrightarrow t | ||
| + | </math> | ||
| + | y la integral inmediata | ||
| + | <center> | ||
| + | <math> | ||
| + | \int t^{-j} \cdot \mathrm{d}t = \frac{t^{1 - j}}{1 - j} + cte. | ||
| + | </math> | ||
| + | </center> | ||
| + | Por otra parte, la integral | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{B_i \cdot x + C_i}{\mathrm{Q}_i \left( \, x \, \right)} \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | se resuelve descomponiendola | ||
| + | en otras dos: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{B_i \cdot x + C_i}{\mathrm{Q}_i \left( \, x \, \right)} \cdot | ||
| + | \mathrm{d}x = | ||
| + | \int \frac{B_i \cdot x}{\mathrm{Q}_i \left( \, x \, \right)} | ||
| + | \cdot \mathrm{d}x | ||
| + | + \int \frac{C_i}{\mathrm{Q}_i \left( \, x \, \right)} \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | La primera de ellas se resuelve mediante el cambio de variable | ||
| + | <math> | ||
| + | \mathrm{Q}_i \left( \, x \, \right) \longrightarrow t | ||
| + | </math>: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{B_i \cdot x}{Q_i | ||
| + | \left( \, x \, \right)} \cdot \mathrm{d}x | ||
| + | = G_i \cdot \log \left| \, \mathrm{Q}_i \left( \, x \, \right)\right| + \mathrm{cte.} | ||
| + | </math> | ||
| + | </center> | ||
| + | donde | ||
| + | <math> | ||
| + | G_i | ||
| + | </math> | ||
| + | es una constante. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para resolver la segunda integral ponemos el polinomio | ||
| + | <math> | ||
| + | \mathrm{Q}_i \left( \, x \, \right) | ||
| + | </math> | ||
| + | de la forma: | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{Q}_i \left( \, x \, \right) = D_i \cdot | ||
| + | \left( | ||
| + | \left( | ||
| + | \, \frac{x + E_i}{F_i} \, | ||
| + | \right)^2 | ||
| + | + 1 \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | y hacemos el cambio de variable | ||
| + | <math> | ||
| + | \frac{x + E_i}{F_i} \longrightarrow t | ||
| + | </math>: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{C_i}{Q_i\left( \, x \, \right)} \cdot \mathrm{d}x = | ||
| + | \int \frac{C_i}{D_i \cdot | ||
| + | \left( | ||
| + | \left( | ||
| + | \, \frac{x + E_i}{F_i} \, | ||
| + | \right)^2 | ||
| + | + 1 \, | ||
| + | \right)} \cdot \mathrm{d}x | ||
| + | = \frac{C_i \cdot F_i}{D_i} \cdot \mathrm{arctan} \left( \, | ||
| + | \frac{x + E_i}{F_i} \, \right) + \mathrm{cte.} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Utilicemos el metodo que se acaba de describir para resolver la siguiente | ||
| + | integral: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{x^5}{x^4 - x^3 - x + 1} \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como el polinomio dividendo ( el polinomio en el numerador, | ||
| + | <math> | ||
| + | \mathrm{D} \left( \, x \, \right) = x^5 | ||
| + | </math> | ||
| + | ) es de grado mayor que el polinomio divisor ( el polinomio en el | ||
| + | denominador, | ||
| + | <math> | ||
| + | \mathrm{d}\left( \, x \, \right) = x^4 - x^3 - x + 1 | ||
| + | </math> | ||
| + | ), lo primero que hacemos es dividir ambos polinomios para obtener el | ||
| + | cociente | ||
| + | <math> | ||
| + | \mathrm{C} \left( \, x \, \right) | ||
| + | </math> | ||
| + | y el resto | ||
| + | <math> | ||
| + | \mathrm{R} \left( \, x \, \right) | ||
| + | </math> | ||
| + | de la división. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \frac{D \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} = | ||
| + | \mathrm{C} \left( \, x \, \right) + \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{d} \left( \, | ||
| + | x \, \right)} | ||
| + | </math> | ||
| + | </center> | ||
| + | Al hacer la división obtenemos que | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{rl} | ||
| + | \mathrm{C} \left( \, x \, \right) & = x + 1 | ||
| + | \\ | ||
| + | \mathrm{R} \left( \, x \, \right) & = x^3 + x^2 - 1 | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Por lo tanto | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{\mathrm{D} \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} | ||
| + | \cdot \mathrm{d}x | ||
| + | = | ||
| + | \int \mathrm{C}\left( \, x \, \right) \cdot \mathrm{d}x + \int | ||
| + | \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} | ||
| + | \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | con | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{C}\left( \, x \, \right) \cdot \mathrm{d}x = \int | ||
| + | x \cdot \mathrm{d}x + \int 1 \cdot \mathrm{d}x = \frac{x^2}{2} + x + \mathrm{cte.} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Pasemos ahora a resolver la integral | ||
| + | <math> | ||
| + | \int | ||
| + | \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} | ||
| + | \cdot \mathrm{d}x | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para ello, lo primero que hacemos es factorizar el polinomio | ||
| + | <math> | ||
| + | \mathrm{d} \left( \, x \, \right) | ||
| + | </math>: | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{d} \left( \, x \, \right) = | ||
| + | \left( | ||
| + | \, x^2 + x + 1 \, | ||
| + | \right) | ||
| + | \cdot | ||
| + | \left( | ||
| + | \, x - 1 \, | ||
| + | \right) | ||
| + | ^2 | ||
| + | </math> | ||
| + | </center> | ||
| + | Con lo cual existen números reales | ||
| + | <math> | ||
| + | A, \, B | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | C | ||
| + | </math> | ||
| + | tales que: | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} = | ||
| + | \frac{A}{x - 1} + \frac{B}{\left( \, x - 1 \, \right)^2} + \frac{Cx + D}{x^2 + x + 1} | ||
| + | </math> | ||
| + | </center> | ||
| + | A continuación calculamos los valores de | ||
| + | <math> | ||
| + | A, \, B | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | C | ||
| + | </math> | ||
| + | para que la igualdad anterior sea cierta: | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{A}{x - 1} + \frac{B}{\left( \, x - 1 \, \right)^2} + \frac{Cx + D}{x^2 + x + 1} = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \frac{A \cdot \left( \, x - 1 \, \right)\cdot \left( \, x^2 + x + 1 \, | ||
| + | \right) + B \cdot \left( \, x^2 + x + 1 \, \right) + \left( \, Cx + D \, | ||
| + | \right) \cdot \left( \, x-1 \, | ||
| + | \right)^2}{\mathrm{d} \left( \, x \, \right)} = \frac{\mathrm{R} \left( \, x | ||
| + | \, \right)}{\mathrm{d} \left( \, x \, \right)} \Rightarrow | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \Rightarrow A \cdot \left( \, x - 1 \, \right)\cdot \left( \, x^2 + x + 1 \, | ||
| + | \right) + B\cdot \left( \, x^2 + x + 1 \, \right) + \left( \, Cx + D \, | ||
| + | \right) \cdot \left( \, x-1 \, | ||
| + | \right)^2 = \mathrm{R} \left( \, x \, | ||
| + | \right) \Rightarrow | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \Rightarrow A \cdot \left( \, x^3 - 1 \, \right) + B \cdot | ||
| + | \left( | ||
| + | \, x^2 + x + 1 \, | ||
| + | \right) | ||
| + | + \left( \, Cx + D \, \right) \cdot ( x^2 - 2x + 1 ) = x^3 + x^2 - 1 \Rightarrow | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \Rightarrow \left( \, A + C \, \right) \cdot x^3 + \left( \, B - 2C + D \, \right) \cdot x^2 + \left( \, | ||
| + | B + C - 2D \, \right) \cdot x + \left( \, -A + B + D \, \right) = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = x^3 + x^2 - 1 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Dos polinomios son iguales si, y solo si, sus coeficientes y terminos independientes | ||
| + | son iguales ( ambos polinomios tienen el mismo grado, digamos | ||
| + | <math> | ||
| + | m | ||
| + | </math>, | ||
| + | y el coeficiente de | ||
| + | <math> | ||
| + | x^n | ||
| + | </math> | ||
| + | en uno de los polinomios es el coeficiente de | ||
| + | <math> | ||
| + | x^n | ||
| + | </math> | ||
| + | en el otro polinomio, para | ||
| + | <math> | ||
| + | n = 0, \, 1, \, \ldots, \, m | ||
| + | </math> | ||
| + | ). Así, se tiene que: | ||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}{rl} | ||
| + | A + C & = 1 | ||
| + | \\ | ||
| + | B + D - 2C & = 1 | ||
| + | \\ | ||
| + | B + C - 2D & = 0 | ||
| + | \\ | ||
| + | -A + B + D & = -1 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | La solución de este [[Sistemas de ecuaciones lineales|sistema de ecuaciones]] | ||
| + | es: | ||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}{rl} | ||
| + | A & = \frac{4}{3} | ||
| + | \\ | ||
| + | B & = \frac{1}{3} | ||
| + | \\ | ||
| + | C & = -\frac{1}{3} | ||
| + | \\ | ||
| + | D & = 0 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | De este modo: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{\mathrm{R} \left( \, x \, \right)}{\mathrm{d} \left( \, x \, \right)} | ||
| + | \cdot \mathrm{d}x = \frac{4}{3} \cdot \int \frac{\mathrm{d}x}{x - 1} + | ||
| + | \frac{1}{3} \int\frac{\mathrm{d}x}{\left( \, x - 1 \, \right)^2} - | ||
| + | \frac{1}{3} \cdot \int \frac{x \cdot \mathrm{d}x}{x^2 + x + 1} | ||
| + | </math> | ||
| + | </center> | ||
| + | Las primeras dos integrales en el miembro de la derecha las podemos resolver con | ||
| + | el cambio de variable | ||
| + | <math> | ||
| + | t = x - 1 | ||
| + | </math>: | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{rl} | ||
| + | \int \frac{\mathrm{d}x}{x - 1} & = \int \frac{\mathrm{d}t}{t} = \mathrm{Ln} \left| | ||
| + | \, t \, \right| + \mathrm{cte.} = \mathrm{Ln} \left| \, x - 1 \, \right| + | ||
| + | \mathrm{cte.} | ||
| + | \\ | ||
| + | \int \frac{\mathrm{d}x}{\left( \, x - 1 \, \right)^2} & = \int | ||
| + | \frac{\mathrm{d}t}{t^2} = -\frac{1}{t} + | ||
| + | \mathrm{cte.} = -\frac{1}{x - 1} + \mathrm{cte.} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Para finalizar el ejemplo calculamos la última integral: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{x \cdot \mathrm{d}x}{x^2 + x + 1} = | ||
| + | \int \frac{x \cdot \mathrm{d}x}{\left( \, x + \frac{1}{2} \, \right)^2 + 3 / 4} | ||
| + | = | ||
| + | \int \frac{4}{3} \cdot \frac{x \cdot \mathrm{d}x}{\left( \, \frac{2}{\sqrt{3}} | ||
| + | \left( \, x + \frac{1}{2} \, \right) \right)^2 + 1} = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \frac{4}{3} \cdot \int \frac{ \left( \, \frac{3u}{4} -\frac{\sqrt{3}}{4} \, | ||
| + | \right) \cdot \mathrm{d}u}{u^2 + 1} = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \frac{1}{2} \cdot \int \frac{2u \cdot \mathrm{d}u}{u^2 + 1} - \frac{1}{\sqrt{3}} \cdot \int \frac{\mathrm{d}u}{u^2 + 1} | ||
| + | = \frac{1}{2} \cdot \mathrm{Ln} \left( \, u^2 + 1 \, \right) - | ||
| + | \frac{1}{\sqrt{3}} \cdot \mathrm{arctan} \left( \, u \, \right) + \mathrm{cte.} | ||
| + | = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{1}{2} \cdot \mathrm{Ln} \left( \frac{4}{3} \cdot \left( \, x + \frac{1}{2} \, \right)^2 + 1 \, \right) - | ||
| + | \frac{1}{\sqrt{3}} \cdot \mathrm{arctan} \left( \, \frac{2}{\sqrt{3}} | ||
| + | \left( | ||
| + | \, x + \frac{1}{2} \, | ||
| + | \right) \right) + \mathrm{cte.} | ||
| + | </math> | ||
| + | </center> | ||
| + | donde se ha utilizado el cambio de variable: | ||
| + | <center> | ||
| + | <math> | ||
| + | u = \frac{2}{\sqrt{3}} | ||
| + | \left( | ||
| + | \, x + \frac{1}{2} \, | ||
| + | \right) | ||
| + | \left( | ||
| + | \, \Rightarrow x \cdot \mathrm{d}x = \left( \, \frac{\sqrt{3}}{2} \cdot u - | ||
| + | \frac{1}{2} \, \right) \cdot \frac{\sqrt{3}}{2} \cdot \mathrm{d}u \, | ||
| + | = \left( \, \frac{3}{4} \cdot u - | ||
| + | \frac{\sqrt{3}}{4} \, \right) \cdot \mathrm{d}u \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Integrales de funciones trigonométricas== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para resolver este tipo de integrales se utilizan amenudo las igualdades que se estudian | ||
| + | en trigonometría. Tambien se utilizan los cambios de variables | ||
| + | <math> | ||
| + | t = \mathrm{cos} \left( \, x \, \right) | ||
| + | </math>, | ||
| + | | ||
| + | <math> | ||
| + | t = \mathrm{sen} \left( \, x \, \right) | ||
| + | </math> | ||
| + | o | ||
| + | <math> | ||
| + | t = \mathrm{tan} \left( \, x \, \right) | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo 1=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Resolvamos la integral | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{sen}^2 \left( \, x \, \right) \cdot \mathrm{cos}^2 \left( \, x \, | ||
| + | \right) \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | Para ello tenemos en cuenta que | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{sen} \left( \, 2x \, \right) = 2 \cdot \mathrm{sen} \left( \, x \, | ||
| + | \right) \cdot \mathrm{cos} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | con lo cual | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{sen}^2 \left( \, x \, \right) \cdot \mathrm{cos}^2 \left( \, x \, | ||
| + | \right) \cdot \mathrm{d}x = | ||
| + | \frac{1}{4} \cdot \int \mathrm{sen}^2 \left( \, 2x \, \right) \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | Como | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{cos} \left( \, 2x \, \right) = \mathrm{cos}^2 \left( \, x \, \right) - | ||
| + | \mathrm{sen}^2 | ||
| + | \left( \,x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | y como | ||
| + | <center> | ||
| + | <math> | ||
| + | 1 = \mathrm{cos}^2 \left( \, x \, \right) + \mathrm{sen}^2 \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | Despejando | ||
| + | <math> | ||
| + | \mathrm{cos}^2 \left( \, x \, \right) | ||
| + | </math> | ||
| + | de esta última igualdad y sustituyendolo en la anterior, se tiene que | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{cos} \left( \, 2x \, \right) = 1 - 2 \cdot \mathrm{sen}^2 \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | Sustituyendo en esta igualdad | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | por | ||
| + | <math> | ||
| + | 2x | ||
| + | </math> | ||
| + | y despejando | ||
| + | <math> | ||
| + | \mathrm{sen}^2 \left( \, 2x \, \right) | ||
| + | </math> | ||
| + | se llega a que | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{sen}^2 \left( \, 2x \, \right) = \frac{1 - \mathrm{cos} \left( \, 4x \, \right)}{2} | ||
| + | </math> | ||
| + | </center> | ||
| + | Así | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{sen}^2 \left( \, 2x \, \right) \cdot \mathrm{d}x = | ||
| + | \int \frac{1 - \mathrm{cos} \left( \, 4x \, \right)}{2} \mathrm{d}x = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \int \frac{\mathrm{d}x}{2} - \frac{1}{2} \int \mathrm{cos} \left( \, 4x \, \right) \cdot \mathrm{d}x = | ||
| + | \frac{x}{2} - \frac{\mathrm{sen} \left( \, 4x \, \right)}{8} + \mathrm{cte.} | ||
| + | </math> | ||
| + | </center> | ||
| + | La última integral se calcula con el cambio de variable | ||
| + | <math> | ||
| + | u = 4x | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo 2=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Resolvamos ahora la siguiente integral: | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{\mathrm{sen} \left( \, x \, \right)}{\mathrm{cos}^3 \left( \, x \, | ||
| + | \right)} \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | mediante el cambio de variable | ||
| + | <center> | ||
| + | <math> | ||
| + | t = \mathrm{tan} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | Definiendo | ||
| + | <math> | ||
| + | t | ||
| + | </math> | ||
| + | de esta manera resulta que | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \frac{\mathrm{sen} \left( \, x \, \right)}{\mathrm{cos}^3 \left( \, x \, | ||
| + | \right)} \cdot \mathrm{d}x = | ||
| + | \int t \cdot \mathrm{d}t = \frac{t^2}{2} + C = \frac{\mathrm{tan}^2 \left( \, x \, \right)}{2} + C | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ya que | ||
| + | <center> | ||
| + | <math> | ||
| + | t = \mathrm{tan} \left( \, x \, \right) \Rightarrow | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | t = \frac{\mathrm{sen} \left( \, x \, \right)}{\mathrm{cos} \left( \, x \, | ||
| + | \right)} | ||
| + | \\ | ||
| + | \frac{\mathrm{d}t}{\mathrm{d}x} = \frac{1}{\mathrm{cos}^2 \left( \, x \, \right)} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
Revisión actual
Tabla de contenidos |
Introducción
No todos los métodos de integración son adecuados para todas las integrales. La habilidad de ver cuál es el método de integración más idóneo para calcular una integral se adquiere resolviendo muchas integrales.
Integración por partes
La fórmula para la derivada de un producto es:
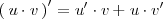
Despejando el último sumando, queda:
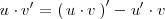
Si integramos en los dos miembros, se obtiene:
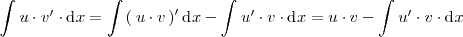
La última igualdad es cierta porque una primitiva de la derivada de una función es esa misma función.
Esta fórmula permite calcular la integral
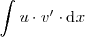 a partir de la integral
a partir de la integral
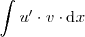 .
.
Para que sea de utilidad el utilizar este metodo es necesario que nos resulte
mas sencilla de resolver la integral
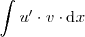 que la integral de partida,
que la integral de partida,
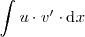 .
.
Ejemplo
Calculemos la integral
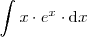
por partes.
Si hacemos
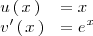
se tiene que
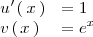
Utilizando la fórmula que hemos visto antes
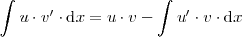
se deduce que
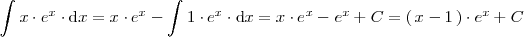
Método de sustitución
Supongamos que queremos resolver una integral del tipo:
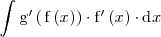
Una manera de resolver un problema de este tipo es haciendo el cambio de variable
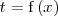
La nueva variable
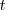 es una función de
es una función de
 ,
con lo cual podemos hablar de la derivada de
,
con lo cual podemos hablar de la derivada de
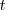 con respecto de
con respecto de
 , que se puede escribir como un cociente de diferenciales:
, que se puede escribir como un cociente de diferenciales:
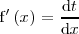
Despejando
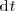 en la igualdad anterior, se deduce que
en la igualdad anterior, se deduce que
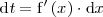
Sustituyendo
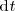 por
por
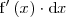 y
y
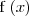 por
por
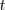 en
en
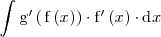
se tiene que
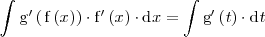
Integrando obtenemos una primitiva
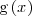 de
de
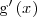 .
.
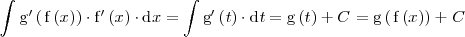
Las igualdades anteriores resumen en que consiste el metodo de sustitución. El
método de sustitución es util en tanto en cuanto sea relativamente facil encontrar una primitiva
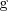 de
de
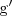 .
.
Ejemplo
Calculemos mediante el método de sustitución la integral
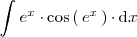
Para ello utilizamos las formulas dadas en la descripción del metodo de sustitución con
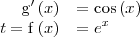
Observese que
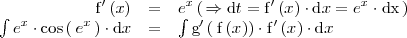
En este caso, una primitiva de
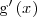 es
es
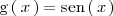
Por lo tanto
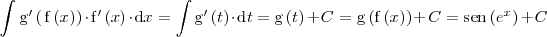
Integración de cocientes de polinomios
Sean
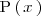 y
y
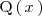 dos polinomios, entonces:
dos polinomios, entonces:
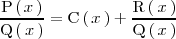
donde
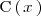 es un polinomio ( el cociente ) y
es un polinomio ( el cociente ) y
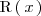 es otro polinomio ( el resto ) de grado menor al grado de
es otro polinomio ( el resto ) de grado menor al grado de
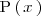 .
.
Si el grado de
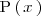 es menor que el grado de
es menor que el grado de
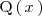 ,
entonces
,
entonces
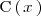 es cero y
es cero y
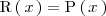 .
.
Como
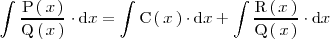
nos podemos restringir al caso en el que el grado del polinomio divisor,
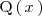 ,
es mayor que grado del polinomio dividendo,
,
es mayor que grado del polinomio dividendo,
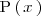 .
.
Para resolver este tipo de integrales lo primero que hay que hacer es
factorizar
el polinomio divisor
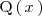 .
.
Al factorizar
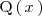 lo podemos poner como un producto de polinomios de grado
uno y/o de grado dos:
lo podemos poner como un producto de polinomios de grado
uno y/o de grado dos:
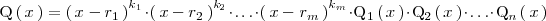
donde

son todas las raices reales de
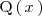 y
y
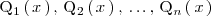
son polinomios de grado dos irreducibles ( sin raices reales ).
De esta forma
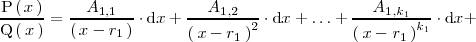
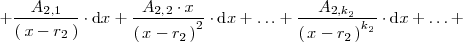
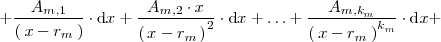
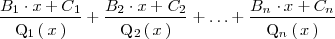
Donde hemos seguido la siguiente notación:
1
.
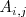 es la constante a la que divide
es la constante a la que divide
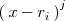 .
.
2
.
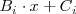 es el polinomio de grado uno al que divide
es el polinomio de grado uno al que divide
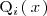 .
.
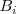 y
y
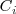 son constantes ( números reales que no dependen de
son constantes ( números reales que no dependen de
 ).
).
Por lo tanto, la integral de
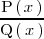 es la suma de las integrales de las fracciones mas simples en las que
hemos descompuesto
es la suma de las integrales de las fracciones mas simples en las que
hemos descompuesto
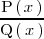 .
.
Estas integrales mas simples son casi inmediatas. Así
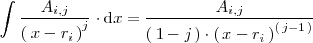
Esta integral se puede resolver utilizando el cambio de variable
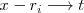 y la integral inmediata
y la integral inmediata
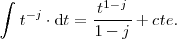
Por otra parte, la integral
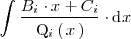
se resuelve descomponiendola en otras dos:
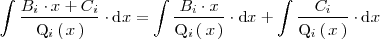
La primera de ellas se resuelve mediante el cambio de variable
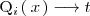 :
:
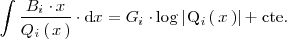
donde
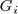 es una constante.
es una constante.
Para resolver la segunda integral ponemos el polinomio
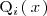 de la forma:
de la forma:
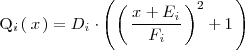
y hacemos el cambio de variable
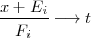 :
:
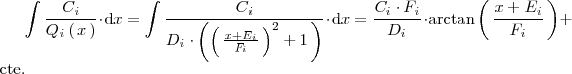
Ejemplo
Utilicemos el metodo que se acaba de describir para resolver la siguiente integral:
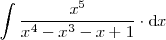
Como el polinomio dividendo ( el polinomio en el numerador,
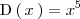 ) es de grado mayor que el polinomio divisor ( el polinomio en el
denominador,
) es de grado mayor que el polinomio divisor ( el polinomio en el
denominador,
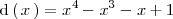 ), lo primero que hacemos es dividir ambos polinomios para obtener el
cociente
), lo primero que hacemos es dividir ambos polinomios para obtener el
cociente
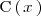 y el resto
y el resto
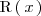 de la división.
de la división.
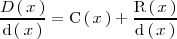
Al hacer la división obtenemos que
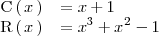
Por lo tanto
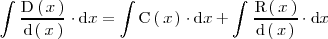
con
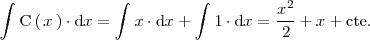
Pasemos ahora a resolver la integral
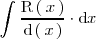 .
.
Para ello, lo primero que hacemos es factorizar el polinomio
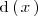 :
:
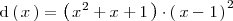
Con lo cual existen números reales
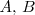 y
y
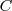 tales que:
tales que:
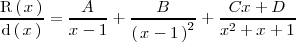
A continuación calculamos los valores de
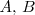 y
y
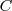 para que la igualdad anterior sea cierta:
para que la igualdad anterior sea cierta:
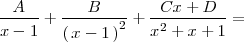
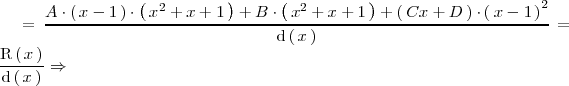
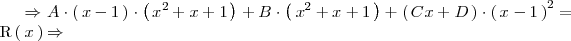
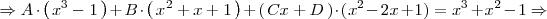
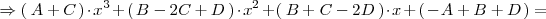
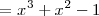
Dos polinomios son iguales si, y solo si, sus coeficientes y terminos independientes
son iguales ( ambos polinomios tienen el mismo grado, digamos
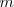 ,
y el coeficiente de
,
y el coeficiente de
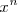 en uno de los polinomios es el coeficiente de
en uno de los polinomios es el coeficiente de
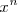 en el otro polinomio, para
en el otro polinomio, para
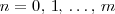 ). Así, se tiene que:
). Así, se tiene que:
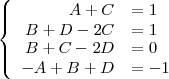
La solución de este sistema de ecuaciones es:
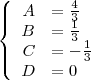
De este modo:
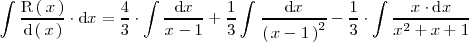
Las primeras dos integrales en el miembro de la derecha las podemos resolver con
el cambio de variable
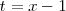 :
:
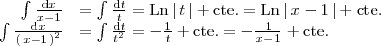
Para finalizar el ejemplo calculamos la última integral:
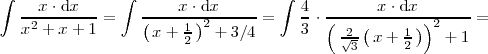
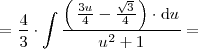
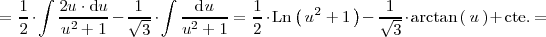
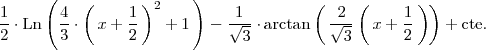
donde se ha utilizado el cambio de variable:
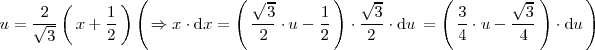
Integrales de funciones trigonométricas
Para resolver este tipo de integrales se utilizan amenudo las igualdades que se estudian
en trigonometría. Tambien se utilizan los cambios de variables
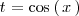 ,
,
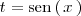 o
o
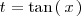 .
.
Ejemplo 1
Resolvamos la integral
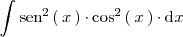
Para ello tenemos en cuenta que
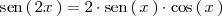
con lo cual
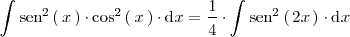
Como
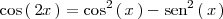
y como
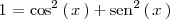
Despejando
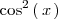 de esta última igualdad y sustituyendolo en la anterior, se tiene que
de esta última igualdad y sustituyendolo en la anterior, se tiene que
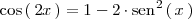
Sustituyendo en esta igualdad
 por
por
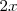 y despejando
y despejando
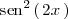 se llega a que
se llega a que
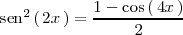
Así
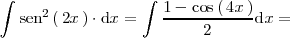
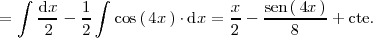
La última integral se calcula con el cambio de variable
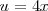 .
.
Ejemplo 2
Resolvamos ahora la siguiente integral:
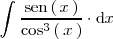
mediante el cambio de variable
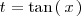
Definiendo
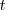 de esta manera resulta que
de esta manera resulta que
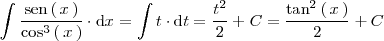
ya que