Integrales inmediatas
De Wikillerato
(Diferencias entre revisiones)
| (Una edición intermedia no se muestra.) | |||
| Línea 8: | Línea 8: | ||
! Función <math>F \,\!</math>: primitiva de <math>f \,\!</math> | ! Función <math>F \,\!</math>: primitiva de <math>f \,\!</math> | ||
| - | ! | + | ! Función <math>f \,\!</math>: derivada de <math>F \,\!</math> |
| - | + | ||
| - | + | ||
| - | + | ||
|- | |- | ||
|| <math>f\left(x\right) = \frac {x^{n+1}}{n+1} + k \,\!</math> | || <math>f\left(x\right) = \frac {x^{n+1}}{n+1} + k \,\!</math> | ||
Revisión actual
Aquí están las principales funciones primitivas:
Función 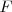 : primitiva de : primitiva de 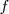
| Función 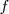 : derivada de : derivada de 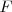
|
|---|---|
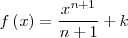
| 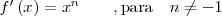
|
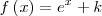
| 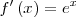
|
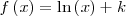
| 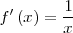
|
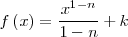
| 
|
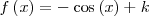
| 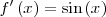
|
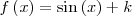
| 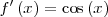
|
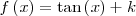
| 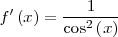
|
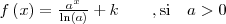
| 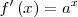
|
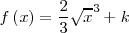
| 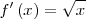
|
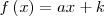
| 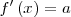
|
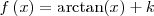
| 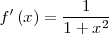
|



