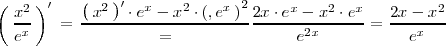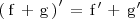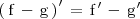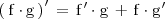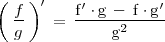Propiedades de las derivadas
De Wikillerato
(Diferencias entre revisiones)
(→Derivada de un cociente de funciones) |
|||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 17: | Línea 17: | ||
Si | Si | ||
<math> | <math> | ||
| - | \mathrm{f} \left( \, x \, \right) = | + | \mathrm{f} \left( \, x \, \right) = 1, \, \forall x \in \mathbb{R} |
</math>, | </math>, | ||
entonces | entonces | ||
| Línea 54: | Línea 54: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \left( \, \mathrm{f}_1 + \mathrm{f}_n + \ldots + \mathrm{f}_n \, \right) = | + | \left( \, \mathrm{f}_1 + \mathrm{f}_n + \ldots + \mathrm{f}_n \, \right)^\prime = |
\mathrm{f}_1^\prime + \mathrm{f}_n^\prime + \ldots + \mathrm{f}_n^\prime | \mathrm{f}_1^\prime + \mathrm{f}_n^\prime + \ldots + \mathrm{f}_n^\prime | ||
</math> | </math> | ||
| Línea 184: | Línea 184: | ||
\, \frac{x^2}{e^x} \, | \, \frac{x^2}{e^x} \, | ||
\right) | \right) | ||
| - | ^\prime \, = \, \frac{\left( \, x^2 \, \right)^\prime \cdot e^x - x^2\cdot\left( | + | ^\prime \, = \, \frac{\left( \, x^2 \, \right)^\prime \cdot e^x - x^2\cdot\left(, e^x \, \right)^2} = |
| - | + | ||
\frac{2x \cdot e^x - x^2 \cdot e^x }{e^{2x}} = \frac{2x - x^2}{e^x} | \frac{2x \cdot e^x - x^2 \cdot e^x }{e^{2x}} = \frac{2x - x^2}{e^x} | ||
</math> | </math> | ||
Revisión actual
Tabla de contenidos |
Derivada una función constante
La derivada de una función constante es cero.
Ejemplo
Si
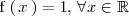 ,
entonces
,
entonces
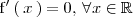
Derivada de una suma de funciones
La derivada de la suma de dos funciones es igual a la suma de las derivadas de dichas funciones:
Este resultado, se puede ampliar a cualquier número de funciones:
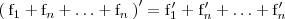
Derivada de una diferencia de funciones
La derivada de la diferencia de dos funciones es igual a la diferencia de las derivadas de dichas funciones:
Ejemplo
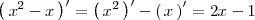
Derivada de un producto de funciones
La derivada del producto de dos funciones,
 y
y
 , viene dada por la fórmula:
, viene dada por la fórmula:
Ejemplo
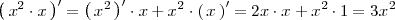
Observese que
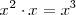 y que la derivada de
y que la derivada de
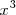 es precisamente
es precisamente
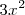 .
.
Derivada de un cociente de funciones
La derivada del cociente
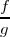 viene dada por la fórmula:
viene dada por la fórmula:
Ejemplo