Eje radical de dos circunferencias
De Wikillerato
(→Eje radical de dos circunferencias) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 9: | Línea 9: | ||
Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical: | Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical: | ||
| - | + | <h4>Eje radical de dos circunferencias secantes</h4> | |
Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias: | Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias: | ||
| Línea 16: | Línea 16: | ||
[[Imagen:Eje_radical_circunferencias_secantes.png]] | [[Imagen:Eje_radical_circunferencias_secantes.png]] | ||
| - | + | ||
| + | <h4>Circunferencias tangentes</h4> | ||
Si las circunferencias son tangentes, 1 y 2 serán el mismo punto, por lo que el eje radical pasará por el punto de tangencia de las dos circunferencias, y será perpendicular a la recta que uno los centros de estas: | Si las circunferencias son tangentes, 1 y 2 serán el mismo punto, por lo que el eje radical pasará por el punto de tangencia de las dos circunferencias, y será perpendicular a la recta que uno los centros de estas: | ||
[[Imagen:Eje_radical_circunferencias_tangentes.png]] | [[Imagen:Eje_radical_circunferencias_tangentes.png]] | ||
| + | |||
| + | == Centro radical de tres circunferencias == | ||
| + | |||
| + | El único punto que posee la misma potencia respecto de tres circunferencias es el centro radical. | ||
| + | |||
| + | Este se halla como la intersección de dos ejes radicales. | ||
| + | |||
| + | <h3>Enlaces externos</h3> | ||
| + | |||
| + | :[http://trazoide.com/potencia.html TRAZOIDE. Teoría y ejercicios resueltos de EJES RADICALES y POTENCIA en Dibujo Técnico] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Ver antes Concepto_de_potencia
Tabla de contenidos |
Eje radical de dos circunferencias
Al igual que existe un punto P que tiene una cierta potencia respecto de una circunferencia, existe una recta que tiene igual potencia respecto de dos circunferencias, de centros O1 y O2.
Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical:
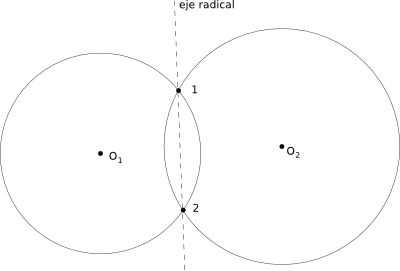
Eje radical de dos circunferencias secantes
Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias:
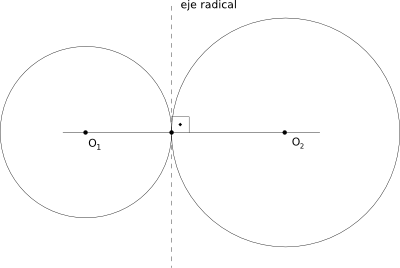
Circunferencias tangentes
Si las circunferencias son tangentes, 1 y 2 serán el mismo punto, por lo que el eje radical pasará por el punto de tangencia de las dos circunferencias, y será perpendicular a la recta que uno los centros de estas:
Centro radical de tres circunferencias
El único punto que posee la misma potencia respecto de tres circunferencias es el centro radical.
Este se halla como la intersección de dos ejes radicales.