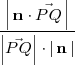Problemas de distancias
De Wikillerato
(→Ejemplo) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 581: | Línea 581: | ||
<br/> | <br/> | ||
| - | + | [[categoría: matemáticas]] | |
Revisión actual
Tabla de contenidos |
Distancia entre dos puntos
La distancia entre dos puntos
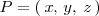 y
y
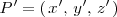 es
es
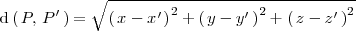
Distancia entre un punto y una recta
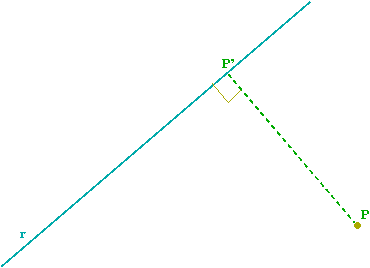
La distancia de un punto
 a una recta
a una recta
 es la distancia entre
es la distancia entre
 y su proyeccion
y su proyeccion
 en la recta
en la recta
 .
.
Ejemplo
Calculemos la distancia del punto
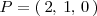 a la recta
a la recta
 de ecuaciones
de ecuaciones
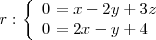
Sea
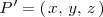 la proyección del punto
la proyección del punto
 en la recta
en la recta
 .
Queremos calcular la distancia de
.
Queremos calcular la distancia de
 a
a
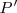 y para ello necesitamos conocer
y para ello necesitamos conocer
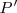 .
.
Para hallar
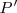 vamos a resolver un sistema de tres ecuaciones, dos de ellas son las de la recta
vamos a resolver un sistema de tres ecuaciones, dos de ellas son las de la recta
 y la otra ecuación procede de igualar a cero el producto escalar del vector
y la otra ecuación procede de igualar a cero el producto escalar del vector
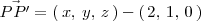
por un vector director de la recta
 .
El producto escalar de ambos vectores es cero porque son perpendiculares (la recta que pasa por
.
El producto escalar de ambos vectores es cero porque son perpendiculares (la recta que pasa por
 y
y
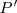 es perpendicular a la recta
es perpendicular a la recta
 ).
).
Podemos obtener un vector director
 de la recta
de la recta
 multiplicando vectorialmente un vector perpendicular al plano
multiplicando vectorialmente un vector perpendicular al plano
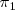 por un vector perpendicular al plano
por un vector perpendicular al plano
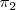 .
.
Un vector
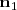 perpendicular al plano
perpendicular al plano
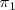 lo podemos obtener de los coeficientes de x, y, z en la ecuación de
lo podemos obtener de los coeficientes de x, y, z en la ecuación de
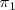 :
:
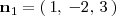
De la misma forma obtenemos un vector
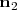 perpendicular al plano
perpendicular al plano
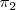 :
:
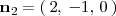
El producto vectorial de ambos vectores,
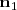 y
y
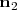 es
es

donde
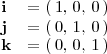
El producto escalar de
 por
por
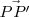 es
es
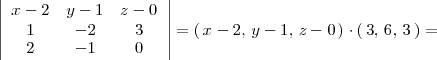
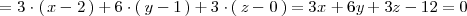
donde la primera fila del determinante es el vector
 .
.
El punto
 es, pues, la solución del sistema de ecuaciones
es, pues, la solución del sistema de ecuaciones
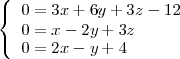
Restando a la tercera ecuación la primera y la segunda se tiene que
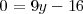
con lo cual
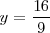 .
Sustituyendo
.
Sustituyendo
 por
por
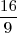 en la tercera ecuación del sistema y despejando
en la tercera ecuación del sistema y despejando
 se llega a que
se llega a que
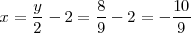
Finalmente, sustituyendo
 por
por
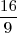 y
y
 por
por
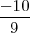 en la segunda ecuación del sistema y despejando
en la segunda ecuación del sistema y despejando
 se llega a que
se llega a que
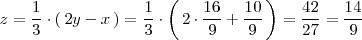
La distancia de
 a
a
 coincide con la distancia de
coincide con la distancia de
 a
a
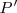 y esta es:
y esta es:
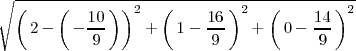
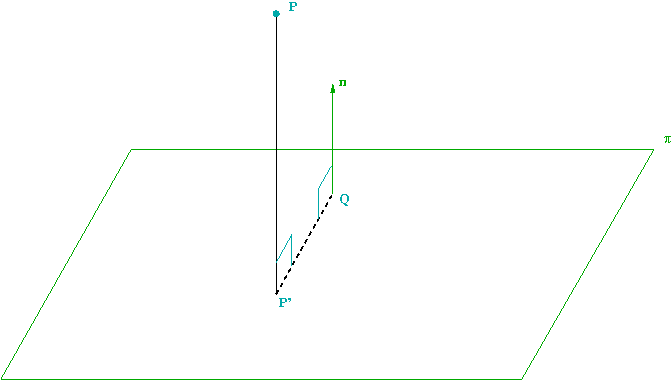
Distancia de un punto a un plano
Sea
 un plano con vector normal
un plano con vector normal
 y al que pertenece el punto
y al que pertenece el punto
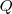 .
.
La distancia de un punto
 al plano
al plano
 es la longitud de la proyección del vector
es la longitud de la proyección del vector
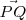 en la dirección normal al plano
en la dirección normal al plano
 ,
que se puede calcular mediante la fórmula:
,
que se puede calcular mediante la fórmula:
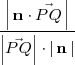
Now we know who the sensilbe one is here. Great post!
Distancia de una recta a un plano
Sea
 una recta paralela a un plano
una recta paralela a un plano
 .
.
Para calcular la distancia de
 a
a
 lo unico que tenemos que hacer es encontrar un punto
lo unico que tenemos que hacer es encontrar un punto
 en la recta
en la recta
 y calcular la distancia de este punto al plano
y calcular la distancia de este punto al plano
 .
.
Distancia entre dos rectas
Para calcular la distancia entre dos rectas,
 y
y
 ,
que se cruzan se procede de la siguiente manera:
,
que se cruzan se procede de la siguiente manera:
En primer lugar, se encuentran vectores directores de ambas rectas,
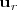 y
y
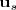 , y un par de puntos,
, y un par de puntos,
 y
y
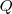 ,
en
,
en
 y en
y en
 ,
respectivamente.
,
respectivamente.
A continuación, se calcula la longitud de la proyección del vector
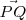 en la dirección normal a un plano paralelo a
en la dirección normal a un plano paralelo a
 y a
y a
 . Esta dirección es la del vector
. Esta dirección es la del vector
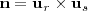
La distancia que buscamos la podemos cacular con la formula