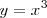Potencias

De Wikillerato

(Diferencias entre revisiones)

Saltar a navegación, búsqueda

Revisión actual

Tabla de contenidos

1 Introducción
2 Propiedades de la potenciación
3 Representación gráfica

Introducción

La potenciación es una operación matemática entre dos números denominados: base a y exponente n.

Se escribe aⁿ y se lee usualmente como «a elevado a n» o «a elevado a la n».

Hay algunos exponentes que se llaman de forma especial, como el 2 que le correponde, al cuadrado o el 3, que le corresponde al cubo.

Su definición varía según como sea el exponente:

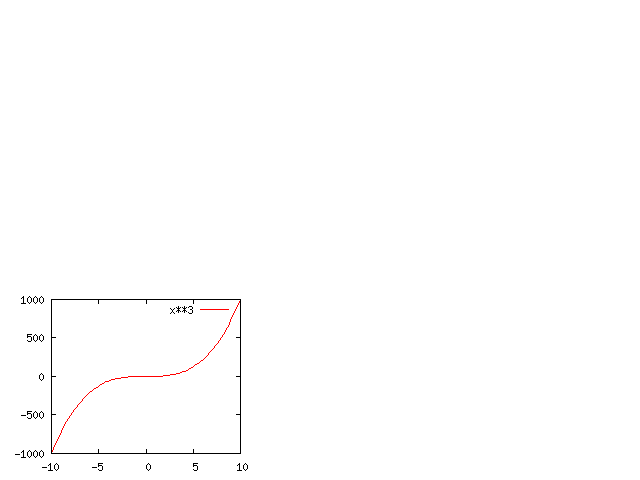
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.

$a^n = \underbrace{a \times \cdots \times a}_n,$

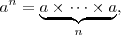
Por ejemplo:

$2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16$ .

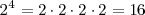Cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.

$a^{-p}= \frac{1}{a^p}$

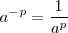
Cuando el exponente es una fracción irreducible n/m, equivale a una raíz:

$a^{\frac{n}{m}} = \sqrt[m]{a^n}$

Cualquier número elevado a el exponente 0 equivale a 1, excepto el caso particular de 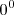$0^0\,$ que, podemos decir que no está definido.

Propiedades de la potenciación

Potencia de exponente 0

Un número (distinto de 0) a, elevado al exponente 0 da como resultado 1, puesto que: $1 = \frac {a^n} {a^n} = a^{n-n} = a^0\,$

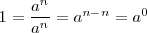
Potencia de exponente 1

Toda potencia de exponente 1 es igual a la base:

$a^1 = a \,$

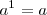
Ejemplo:

$54^1=54 \,$

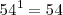
Potencia de exponente negativo

Un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero con exponente positivo: $a^{-n} = a^{0-n} = \frac {a^0}{a^n} = \frac {1}{a^n}\,$

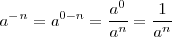
Multiplicación de potencias de igual base

El producto de dos o más potencias de igual base es igual a la base elevada a la suma de los correspondientes exponentes (se escribe la misma base y se suman los exponentes):

$a^m \cdot a^n = a^{m + n}$

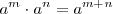
Ejemplos:

$9^3 \cdot 9^2 = 9^{3+2}= 9^5$

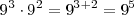
División de potencias de igual base

La división de dos potencias de igual base es igual a la base elevada a la resta de los exponentes respectivos:

$\frac{a^m}{a^n} = a^{m - n}$

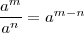
Ejemplo:

$\frac{9^5}{9^3} = 9^{5-3}= 9^2$

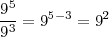
Potencia de un producto

La potencia de un producto es igual al producto de los factores elevados cada uno al exponente de dicha potencia. Es decir, una potencia de base a.b y de exponente n, es igual al factor a elevado a n, multiplicado por el factor b también elevado a n:

$(a \cdot b)^n=a^n \cdot b^n$

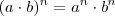
Potencia de una potencia

La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):

${(a^m)}^n = a^{m \cdot n}$

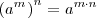
Debido a esto, la notación 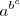$a^{b^c}$ se reserva para significar 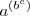$a^{(b^c)}$ ya que 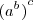${(a^b)}^c$ se puede escribir sencillamente como $a^{bc}\,$ .

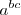Propiedad distributiva

La potenciación es distributiva con respecto a la multiplicación y a la división:

$(a \cdot b)^n = a^n \cdot b^n$

$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}$

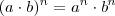
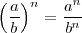
Propiedades que no cumple la potenciación

No es distributiva con respecto a la adición y sustracción, es decir, no se puede distribuir cuando dentro del paréntesis es suma o resta:

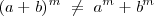
$(a + b)^m \ \neq\ a^m + b^m$

$(a - b)^m \ \neq\ a^m - b^m$

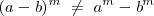
No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes. En general:

$a^b \ \neq\ b^a$

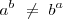
Tampoco cumple la propiedad asociativa:

$a^{b^c}=a^{(b^c)}\ne (a^b)^c=a^{(b\cdot c)}=a^{b c}$

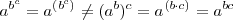
Potencia de base 10

En las potencias con base 10, el resultado será la unidad desplazada tantas posiciones como indique el valor absoluto del exponente: hacia la izquierda si el exponente es negativo, o hacia la derecha si el exponente es positivo.

Ejemplos:

$10^{-5}=0,00001 \,$
$10^{-4}=0,0001 \,$
$10^{-3}=0,001 \,$
$10^{-2}=0,01 \,$
$10^{-1}=0,1 \,$
$10^0=1 \,$
$10^1=10 \,$
$10^2=100 \,$
$10^3=1.000 \,$
$10^4=10.000 \,$
$10^5=100.000 \,$
$10^6=1.000.000\,$

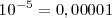
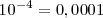
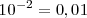
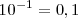
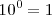
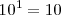
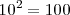
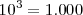
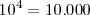
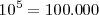
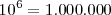
Representación gráfica

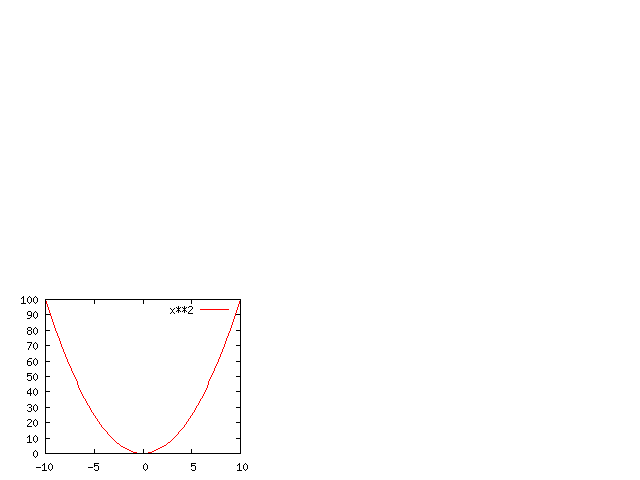
La representación gráfica de una potencia par tiene la forma de una parábola. Su vértice se sitúa en el punto (0, 0), es decreciente en el segundo cuadrante y creciente en el primero.

Ejemplo:

$y = x^2$

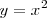
La representación gráfica de una potencia impar son dos ramas de parábola. Tiene un punto de inflexión en el vértice (0, 0), es siempre creciente, y ocupa el tercer y primer cuadrante.

Ejemplo:

$y = x^3$