Logaritmos
De Wikillerato
(Página nueva: En matemáticas, el '''logaritmo''' de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número del que queremos cal...) |
|||
| (4 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | En matemáticas, el '''logaritmo''' de un número en una base determinada es el | + | En matemáticas, el '''logaritmo''' de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número del que queremos calcular el logaritmo. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10<sup>3</sup> = 10×10×10. |
| - | De la misma manera que la operación opuesta de la | + | De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, los logaritmos son la operación inversa a la potencias. |
== Definición == | == Definición == | ||
Dados dos números cualquiera ('''x''' , '''n''') la operación '''logaritmo''' <math>log_n(x)</math> tendrá como resultado otro número ''y''; cuyo valor es''''el número al que hay que elevar y para que: | Dados dos números cualquiera ('''x''' , '''n''') la operación '''logaritmo''' <math>log_n(x)</math> tendrá como resultado otro número ''y''; cuyo valor es''''el número al que hay que elevar y para que: | ||
| + | |||
<br> | <br> | ||
<math>log_n(x) = y \Leftrightarrow n^y = x</math> | <math>log_n(x) = y \Leftrightarrow n^y = x</math> | ||
| Línea 34: | Línea 35: | ||
::<math> \!\, \sqrt[x]{y} = y^\frac{1}{x} \,</math> | ::<math> \!\, \sqrt[x]{y} = y^\frac{1}{x} \,</math> | ||
| + | <br> | ||
== Elección de la base == | == Elección de la base == | ||
| - | *Se llaman '''logaritmos | + | *Se llaman '''logaritmos neperianos''' (''ln'') al logaritmo en base '''e'''; donde e ≈ 2,71828... |
| - | *Los logaritmos de base 10, son aquellos en que la base es 10 | + | *Los logaritmos de base 10, son aquellos en que la base es 10. |
| - | + | Estos dos son los logaritmos mas comunues, y funcionarían como ya hemos descrito: | |
| - | + | <math>log_{10}(100) = 2 \Leftrightarrow 10^2 = 100</math><br> | |
| + | <math>log_e(148.4131591025766) = ln(148.4131591025766) = 5\Leftrightarrow e^5 = 148.4131591025766</math><br> | ||
| + | Pero también podemos calcular logaritmos de calquier número en cualquier base: | ||
| + | <math>log_2(16) = 4\Leftrightarrow 2^4 = 116</math><br> | ||
| + | |||
| + | |||
| + | <br> | ||
=== Cambio de base === | === Cambio de base === | ||
| - | + | ||
| + | Entonces son comunes los logaritmos en base '''e''' (logaritmo neperiano), base '''10''' (logaritmo común), base '''2''' (logaritmo binario)... La elección de un determinado número como base de los logaritmos no es determinante, ya que todos son proporcionales entre sí. | ||
| + | |||
| + | Es útil la siguiente fórmula que define al ''logaritmo de x en base b'' (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1): | ||
<math>\log_b(x) = \frac {\log_k(x)}{\log_k(b)} \,\!\,</math> | <math>\log_b(x) = \frac {\log_k(x)}{\log_k(b)} \,\!\,</math> | ||
| Línea 54: | Línea 65: | ||
<math>\log_b(x) = \frac {1}{\log_x(b)} \,\!\,</math> | <math>\log_b(x) = \frac {1}{\log_x(b)} \,\!\,</math> | ||
| - | En la práctica, se emplea el logaritmo decimal, que se indica como <math>\log(x)\,\!\,</math>, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada | + | En la práctica, se emplea el logaritmo decimal, que se indica como <math>\log(x)\,\!\,</math>, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido (dB), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces. |
| - | + | ||
| - | + | ||
| + | <br> | ||
== Definición analítica == | == Definición analítica == | ||
| - | |||
| - | |||
| - | + | <gnuplot> | |
| + | set terminal png small transparent | ||
| + | set size 0.4, 0.4 | ||
| + | plot log(x) | ||
| + | </gnuplot> | ||
| - | |||
| - | |||
| - | |||
| - | + | Podemos introducir la función logarítmica como una función y estudiarla como tal. esta función no tiene ni máximos pero si tiene una asíntota en '''x = 0''', este es el motivo por el que el logaritmo de un número negativo no está definido. Ahora estudiaremos todas sus propiedades. | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | <br> | ||
=== Propiedades de la función logarítmica === | === Propiedades de la función logarítmica === | ||
# El dominio de la función <math>\ln(x)\,</math> definida anteriormente es el conjunto de los números reales positivos. | # El dominio de la función <math>\ln(x)\,</math> definida anteriormente es el conjunto de los números reales positivos. | ||
| Línea 80: | Línea 87: | ||
# La tangente <math>T_1\,</math> que pasa por el punto de abscisa 1 de la curva, tiene como ecuación: <math>y = x - 1\,</math>. | # La tangente <math>T_1\,</math> que pasa por el punto de abscisa 1 de la curva, tiene como ecuación: <math>y = x - 1\,</math>. | ||
# La derivada de segundo orden es <math>\ln^{\prime\prime} (x) = {-1}/{x^2}\,</math>, siempre negativa, por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "r" ( <math>\swarrow\,</math> ), es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con <math>T_1\,</math> y <math>T_e\,</math>. | # La derivada de segundo orden es <math>\ln^{\prime\prime} (x) = {-1}/{x^2}\,</math>, siempre negativa, por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "r" ( <math>\swarrow\,</math> ), es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con <math>T_1\,</math> y <math>T_e\,</math>. | ||
| - | # La función logaritmo neperiano es la | + | # La función logaritmo neperiano es la inversa de la función exponencial: <math>f(x) = e^x\;\,</math>. |
| + | <br> | ||
== Propiedades generales == | == Propiedades generales == | ||
| - | # Los números negativos no tienen logaritmo en el campo de los reales, ya que cualquiera sea ''u'', es siempre <math>e^u > 0\,</math> (o <math>10^u > 0\,</math>) y en consecuencia no hay ningún valor de ''u'' que pueda satisfacer <math>e^u = x\,</math> cuando <math>x<0\,</math>, sin embargo, se pueden calcular logaritmos de números negativos | + | # Los números negativos no tienen logaritmo en el campo de los reales, ya que cualquiera sea ''u'', es siempre <math>e^u > 0\,</math> (o <math>10^u > 0\,</math>) y en consecuencia no hay ningún valor de ''u'' que pueda satisfacer <math>e^u = x\,</math> cuando <math>x<0\,</math>, sin embargo, se pueden calcular logaritmos de números negativos. |
# El logaritmo de su base es 1. Así <math>\log_b b=1\,</math> ya que <math>b^1=b\,</math>. | # El logaritmo de su base es 1. Así <math>\log_b b=1\,</math> ya que <math>b^1=b\,</math>. | ||
# El logaritmo de 1 es cero (independientemente de la base). Así <math>\log_b 1=0\,</math> ya que <math>b^0=1\,</math>. | # El logaritmo de 1 es cero (independientemente de la base). Así <math>\log_b 1=0\,</math> ya que <math>b^0=1\,</math>. | ||
# Si 0<''A''<1 entonces <math>\log_b A\,</math> es un logaritmo negativo. Es lógico ya que el logaritmo de 1 es cero, entonces los menores que uno serán negativos por ser la función logarítmica estrictamente creciente. | # Si 0<''A''<1 entonces <math>\log_b A\,</math> es un logaritmo negativo. Es lógico ya que el logaritmo de 1 es cero, entonces los menores que uno serán negativos por ser la función logarítmica estrictamente creciente. | ||
| - | # Las potencias consecutivas de una base forman una | + | # Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Así las potencias de 2 son 1,2,4,8,16...etc y sus exponentes serán 0, 1, 2, 3, 4... etc ya que <math>2^0=1\,</math>, <math>2^1=2\,</math>, <math>2^2=4\,</math>, <math>2^3=8\,</math>, y <math>2^4=16\,</math> etc. Luego <math>\log_2 1=0\,</math>, <math>\log_2 2=1\,</math>, <math>\log_2 4=2\,</math>, <math>\log_2 8=3\,</math> y <math>\log_2 16=4\,</math> etc. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |||
| - | |||
| - | + | [[Category:Matemáticas]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Revisión actual
En matemáticas, el logaritmo de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número del que queremos calcular el logaritmo. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, los logaritmos son la operación inversa a la potencias.
Tabla de contenidos |
Definición
Dados dos números cualquiera (x , n) la operación logaritmo 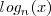 tendrá como resultado otro número y; cuyo valor es'el número al que hay que elevar y para que:
tendrá como resultado otro número y; cuyo valor es'el número al que hay que elevar y para que:
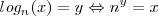
- La base b tiene que ser positiva y distinta de 1
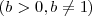 .
.
- x tiene que ser un número positivo
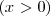 .
.
- n puede ser cualquier número real
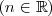 .
.
Por ejemplo:
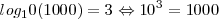
Entonces, en la expresión 103 = 1000, el logaritmo de 1000 en base 10 es 3.
Propiedades de los logaritmos
Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:
Elección de la base
- Se llaman logaritmos neperianos (ln) al logaritmo en base e; donde e ≈ 2,71828...
- Los logaritmos de base 10, son aquellos en que la base es 10.
Estos dos son los logaritmos mas comunues, y funcionarían como ya hemos descrito:
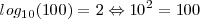
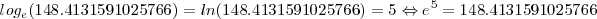
Pero también podemos calcular logaritmos de calquier número en cualquier base:
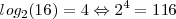
Cambio de base
Entonces son comunes los logaritmos en base e (logaritmo neperiano), base 10 (logaritmo común), base 2 (logaritmo binario)... La elección de un determinado número como base de los logaritmos no es determinante, ya que todos son proporcionales entre sí.
Es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1):
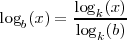
en la que "k" es cualquier base válida. Si hacemos k=x, obtendremos:
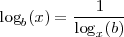
En la práctica, se emplea el logaritmo decimal, que se indica como 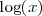 , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido (dB), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.
, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido (dB), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.
Definición analítica
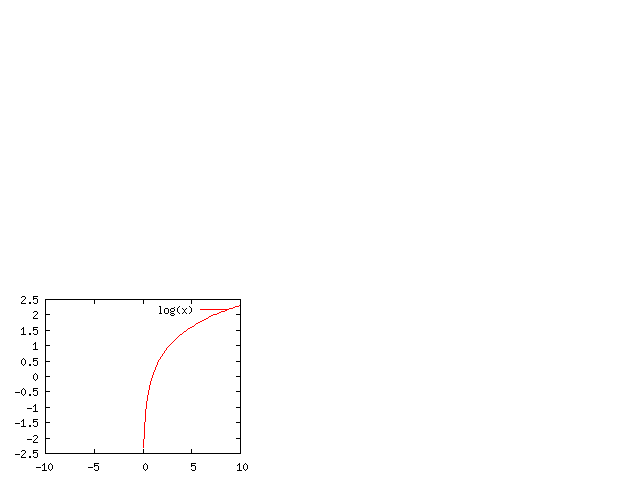
Podemos introducir la función logarítmica como una función y estudiarla como tal. esta función no tiene ni máximos pero si tiene una asíntota en x = 0, este es el motivo por el que el logaritmo de un número negativo no está definido. Ahora estudiaremos todas sus propiedades.
Propiedades de la función logarítmica
- El dominio de la función
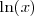 definida anteriormente es el conjunto de los números reales positivos.
definida anteriormente es el conjunto de los números reales positivos.
-
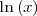 es estrictamente creciente pues su derivada es estrictamente positiva.
es estrictamente creciente pues su derivada es estrictamente positiva.
- Tiene límites infinitos en
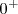 y en
y en 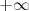 .
.
- La tangente
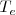 que pasa por el punto de abscisa e de la curva, pasa también por el origen.
que pasa por el punto de abscisa e de la curva, pasa también por el origen.
- La tangente
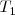 que pasa por el punto de abscisa 1 de la curva, tiene como ecuación:
que pasa por el punto de abscisa 1 de la curva, tiene como ecuación: 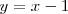 .
.
- La derivada de segundo orden es
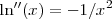 , siempre negativa, por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "r" (
, siempre negativa, por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "r" ( 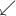 ), es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con
), es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con 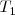 y
y 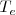 .
.
- La función logaritmo neperiano es la inversa de la función exponencial:
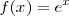 .
.
Propiedades generales
- Los números negativos no tienen logaritmo en el campo de los reales, ya que cualquiera sea u, es siempre
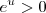 (o
(o 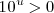 ) y en consecuencia no hay ningún valor de u que pueda satisfacer
) y en consecuencia no hay ningún valor de u que pueda satisfacer 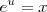 cuando
cuando 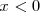 , sin embargo, se pueden calcular logaritmos de números negativos.
, sin embargo, se pueden calcular logaritmos de números negativos.
- El logaritmo de su base es 1. Así
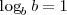 ya que
ya que 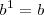 .
.
- El logaritmo de 1 es cero (independientemente de la base). Así
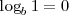 ya que
ya que 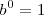 .
.
- Si 0<A<1 entonces
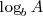 es un logaritmo negativo. Es lógico ya que el logaritmo de 1 es cero, entonces los menores que uno serán negativos por ser la función logarítmica estrictamente creciente.
es un logaritmo negativo. Es lógico ya que el logaritmo de 1 es cero, entonces los menores que uno serán negativos por ser la función logarítmica estrictamente creciente.
- Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Así las potencias de 2 son 1,2,4,8,16...etc y sus exponentes serán 0, 1, 2, 3, 4... etc ya que
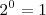 ,
, 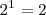 ,
, 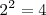 ,
, 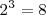 , y
, y 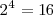 etc. Luego
etc. Luego 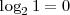 ,
, 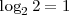 ,
, 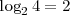 ,
, 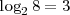 y
y 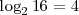 etc.
etc.


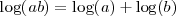
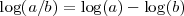
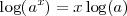
![\!\, \log(\sqrt[x]{y}) = \frac{\log(y)}{x} \, \!\, \log(\sqrt[x]{y}) = \frac{\log(y)}{x} \,](/images/math/math-b34e90ec3b13091f07fad8d4889321c9.png)
![\!\, \sqrt[x]{y} = y^\frac{1}{x} \, \!\, \sqrt[x]{y} = y^\frac{1}{x} \,](/images/math/math-0a0b3045ea44067266ba9ae96f1397a3.png)

