Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Sucesos Independientes

De Wikillerato

(Diferencias entre revisiones)
Revisión actual (11:59 25 feb 2011) (editar) (deshacer)
(→Ejercicios Resueltos)
 
(6 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
__TOC__
__TOC__
 +
 +
==Definición==
 +
 +
<br/>
Decimos que dos sucesos &nbsp;
Decimos que dos sucesos &nbsp;
Línea 44: Línea 48:
<center>
<center>
<math>
<math>
-
A \quad \mathrm{y} \quad B \quad \makebox{son independientes} \Leftrightarrow
+
A \quad \mathrm{y} \quad B \quad \makebox{son independientes} \quad \Leftrightarrow \quad
\mathrm{P}
\mathrm{P}
\left(
\left(
Línea 62: Línea 66:
<br/>
<br/>
-
====Ejemplo====
+
==Ejemplos==
<br/>
<br/>
-
Calcula la probabilidad de que al extraer 3 cartas, con reemplazamiento, de una baraja española, sean todas copas.
+
Calcula la probabilidad de que al extraer 3 cartas, con reemplazamiento, de una baraja española,<br> sean todas copas.
<br/>
<br/>
Línea 122: Línea 126:
Calcula la probabilidad de que al extraer 3 cartas, sucesivamente, de una baraja española, sean todas copas.
Calcula la probabilidad de que al extraer 3 cartas, sucesivamente, de una baraja española, sean todas copas.
 +
 +
<br/>
 +
 +
En este caso, los sucesos &nbsp;
 +
<math>
 +
C_1, \, C_2 \quad \mathrm{y} \quad C_3
 +
</math>
 +
&nbsp; no son independientes.
<br/>
<br/>
Línea 148: Línea 160:
<br/>
<br/>
 +
 +
==Ejercicios Resueltos==
 +
 +
{{problemas}}* [http://www.selectividad.tv/S_M_3_1_3_S_probabilidad_de_aprobar_cuando_solo_se_domina_parte_de_la_asignatura.html Probabilidad de aprobar cuando sólo se domina parte de la asignatura]
 +
* [http://www.selectividad.tv/S_M_3_1_5_S_probabilidad_de_meter_un_gol_en_una_tanda_de_penaltis.html Probabilidad de meter un gol en una tanda de penaltis]
 +
* [http://www.selectividad.tv/S_M_3_1_4_S_probabilidad_de_obtener_dos_numeros_pares_lanzando_dos_dados.html Probabilidad de obtener dos números pares lanzando dos dados]
[[Category:Matemáticas]]
[[Category:Matemáticas]]

Revisión actual

Tabla de contenidos


Definición


Decimos que dos sucesos   A   y   B   son independientes entre sí si la ocurrencia de uno de ellos no modifica la probabilidad del otro, es decir, si:


\mathrm{P} \left( </p> <pre> \, B \, \left| \, A \, \, \right. </pre> <p>\right) \, = \, \mathrm{P} \left( </p> <pre> \, B \, </pre> <p>\right) \qquad \mathrm{o} \qquad \mathrm{P} \left( </p> <pre> \, A \, \left| \, B \, \, \right. </pre> <p>\right) \, = \, \mathrm{P} \left( </p> <pre> \, A \, </pre> <p>\right)


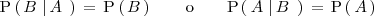
o lo que es lo mismo:


A \quad \mathrm{y} \quad B \quad \makebox{son independientes} \quad \Leftrightarrow \quad \mathrm{P} \left( </p> <pre> \, A \, \cap \, B \, </pre> <p>\right) \, = \, \mathrm{P} \left( </p> <pre> \, A \, </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, B \, </pre> <p>\right)


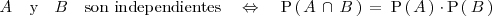
Ejemplos


Calcula la probabilidad de que al extraer 3 cartas, con reemplazamiento, de una baraja española,
 sean todas copas.


Como la carta extraída se vuelve a introducir, los sucesos son independientes y la probabilidad buscada es:


\mathrm{P} \left( </p> <pre> \, C_1 \, \cap C_2 \, \cap C_3 \, </pre> <p>\right) \, = \, \mathrm{P} \left( </p> <pre> \, C_1 \, </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_2 \, \left| \, C_1 \, \right. </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_3 \, \left| \, C_1, \, C_2 \, \right. </pre> <p>\right) </p> <pre>\, = \, \mathrm{P} </pre> <p>\left( </p> <pre> \, C_1 \, </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_2 \, </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_3 \, </pre> <p>\right) </p> <pre>\, = \, \frac{10}{40} \cdot \frac{10}{40} \cdot \frac{10}{40} </pre> <p>


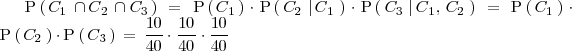
donde 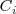  C_i   denota el suceso salir copas en la extracción número   i . 


Calcula la probabilidad de que al extraer 3 cartas, sucesivamente, de una baraja española, sean todas copas.


En este caso, los sucesos   C_1, \, C_2 \quad \mathrm{y} \quad C_3   no son independientes.


\mathrm{P} \left( </p> <pre> \, C_1 \, \cap C_2 \, \cap C_3 \, </pre> <p>\right) \, = \, \mathrm{P} \left( </p> <pre> \, C_1 \, </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_2 \, \left| \, C_1 \, \right. </pre> <p>\right) \cdot \mathrm{P} \left( </p> <pre> \, C_3 \, \left| \, C_1, \, C_2 \, \right. </pre> <p>\right) </p> <pre>\, = \, \frac{10}{40} \cdot \frac{9}{39} \cdot \frac{8}{38} </pre> <p>


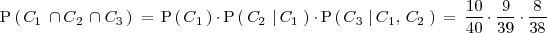
Ejercicios Resueltos

También te pueden interesar los siguientes ejercicios resueltos de selectividad

Obtenido de "http://wikillerato.org/Sucesos_Independientes.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.