Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Límites por la derecha e izquierda

De Wikillerato

(Diferencias entre revisiones)
Revisión actual (09:06 15 dic 2010) (editar) (deshacer)
m (Revertidas las ediciones realizadas por 187.147.0.197 (Talk); a la última edición de 187.146.43.120)
 
(4 ediciones intermedias no se muestran.)
Línea 22: Línea 22:
  y que tiende a  
  y que tiende a  
<math>
<math>
-
x_0
+
x_
</math>
</math>
&nbsp; verifica
&nbsp; verifica
Línea 142: Línea 142:
</math>
</math>
&nbsp; por la izquierda.
&nbsp; por la izquierda.
 +
 +
<br/>
[[Category:Matemáticas]]
[[Category:Matemáticas]]

Revisión actual

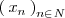Se dice que el limite por la derecha de una función   \mathrm{f}   en el punto   x_0   es   L , si toda sucesión   \left( \, x_n \, \right) _{n \in N}   cuyos terminos son todos mayores que   x_0   y que tiende a   x_   verifica


\lim_{n \to \infty} \mathrm{f} \left( \, x_n \, \right) \, = \, L


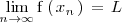
El limite por la derecha se denota por


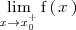\lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right)       o bien       \lim_{{ x \to x_0 \atop x > x_0}} \mathrm{f} \left( \, x \, \right)


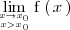
El que la anterior igualdad sea cierta significa que podemos hacer   \mathrm{f} \left( \, x \, \right)   tan cercano a   L   como queramos eligiendo   x   lo suficientemente proximo a   x_0   por la derecha.


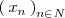Se dice que el limite por la izquierda de una función   \mathrm{f}   en el punto   x_0   es   L , si toda sucesión   \left( \, x_n \, \right) _{n \in N}   cuyos terminos son todos menores que   x_0   y que tiende a   x_0   verifica


\lim_{n \to \infty} \mathrm{f} \left( \, x_n \, \right) \, = \, L


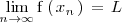
El limite por la izquierda se denota por


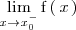\lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right)       o bien       \lim_{{ x \to x_0 \atop x_0 > x}} \mathrm{f} \left( \, x \, \right)


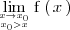
El que la anterior igualdad sea cierta significa que podemos hacer   \mathrm{f} \left( \, x \, \right)   tan cercano a   L   como queramos eligiendo   x   lo suficientemente proximo a   x_0   por la izquierda.


Obtenido de "http://wikillerato.org/L%C3%ADmites_por_la_derecha_e_izquierda.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.