|
|
| (7 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | Un '''''sistema de ecuaciones lineales''''' con incógnitas
| + | {{revisar}} |
| - | <math>
| + | <br> |
| - | \left(
| + | |
| - | \, x_1, \, x_2, \, \ldots, \, x_n \,
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | es un conjunto formado por
| + | |
| - | <math>
| + | |
| - | m
| + | |
| - | </math>
| + | |
| - | igualdades de la forma:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left.
| + | |
| - | \begin{array}{c}
| + | |
| - | a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1
| + | |
| - | \\
| + | |
| - | a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2
| + | |
| - | \\
| + | |
| - | \dotfill
| + | |
| - | \\
| + | |
| - | a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m
| + | |
| - | \end{array}
| + | |
| - | \right\}
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/> | + | |
| - | | + | |
| - | donde los
| + | |
| - | <math>
| + | |
| - | a_{ij}
| + | |
| - | </math>
| + | |
| - | se llaman coeficientes y los
| + | |
| - | <math>
| + | |
| - | b_i
| + | |
| - | </math>
| + | |
| - | , terminos independientes del sistema.
| + | |
| - | | + | |
| - | En los coeficientes
| + | |
| - | <math>
| + | |
| - | a_{ij}
| + | |
| - | </math>
| + | |
| - | , el subindice
| + | |
| - | <math>
| + | |
| - | i
| + | |
| - | </math>
| + | |
| - | indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice
| + | |
| - |
| + | |
| - | <math>
| + | |
| - | j
| + | |
| - | </math>
| + | |
| - | señala de que incognita es coeficiente
| + | |
| - | <math>
| + | |
| - | a_{ij}
| + | |
| - | </math>
| + | |
| - | .
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | El subindice
| + | |
| - | <math>
| + | |
| - | i
| + | |
| - | </math>
| + | |
| - | que aparece en el término
| + | |
| - | <math>
| + | |
| - | b_i
| + | |
| - | </math>
| + | |
| - | , indica la ecuación de la que
| + | |
| - | <math>
| + | |
| - | b_i
| + | |
| - | </math>
| + | |
| - | es término independiente.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | El sistema anterior de
| + | |
| - | <math>
| + | |
| - | m
| + | |
| - | </math>
| + | |
| - | ecuaciones lineales con
| + | |
| - | <math>
| + | |
| - | n
| + | |
| - | </math>
| + | |
| - | incognitas se puede escribir matricialmente de la siguiente forma:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left(
| + | |
| - | \begin{array}[c]{cccc}
| + | |
| - | a_{11} & a_{12} & \ldots & a_{1n}
| + | |
| - | \\
| + | |
| - | a_{21} & a_{22} & \ldots & a_{2n}
| + | |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | a_{m1} & a_{m2} & \ldots & a_{mn}
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | \cdot
| + | |
| - | \left(
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | x_1
| + | |
| - | \\
| + | |
| - | x_2
| + | |
| - | \\
| + | |
| - | \vdots
| + | |
| - | \\
| + | |
| - | x_n
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | \, = \,
| + | |
| - | \left(
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | b_1
| + | |
| - | \\
| + | |
| - | b_2
| + | |
| - | \\
| + | |
| - | \vdots
| + | |
| - | \\
| + | |
| - | b_m
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | De izquierda a derecha, la primera matriz, en la igualdad anterior es la '''''matriz de los coeficientes''''' y la llamaremos
| + | |
| - |
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | , la segunda matriz es la matriz de las incognitas y la llamaremos
| + | |
| - | <math>
| + | |
| - | X
| + | |
| - | </math>
| + | |
| - | . La tercera es la matriz de los terminos indedependientes y la llamaremos
| + | |
| - | <math>
| + | |
| - | B
| + | |
| - | </math>
| + | |
| - | .
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Con esta notación, nuestro sistema de ecuaciones lineales se puede representar de la
| + | |
| - | siguiente manera:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | A \cdot X \, = \, B
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | La
| + | |
| - | '''''matriz ampliada''''' es la matriz de los coeficientes,
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | , a la que se añade la columna de los terminos independientes,
| + | |
| - | <math>
| + | |
| - | B
| + | |
| - | </math>
| + | |
| - | :
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | A|B \, = \,
| + | |
| - | \left(
| + | |
| - | \left.
| + | |
| - | \begin{array}[c]{cccc}
| + | |
| - | a_{11} & a_{12} & \ldots & a_{1n}
| + | |
| - | \\
| + | |
| - | a_{21} & a_{22} & \ldots & a_{2n}
| + | |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | a_{m1} & a_{m2} & \ldots & a_{mn}
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | b_1
| + | |
| - | \\
| + | |
| - | b_2
| + | |
| - | \\
| + | |
| - | \vdots
| + | |
| - | \\
| + | |
| - | b_m
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones. Al conjunto
| + | |
| - | de todas las soluciones del sistema se le llama solución general, y a cada una de las
| + | |
| - | soluciones que forman dicho conjunto, solución particular.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Serán soluciones del sistema todas las n-tuplas
| + | |
| - | <math>
| + | |
| - | \left(
| + | |
| - | \, s_1, \, s_2, \, \ldots, \, s_n \,
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | tales que al sustituir
| + | |
| - | <math>
| + | |
| - | x_i
| + | |
| - | </math>
| + | |
| - | por
| + | |
| - | <math>
| + | |
| - | s_i
| + | |
| - | </math>
| + | |
| - | , para
| + | |
| - | <math>
| + | |
| - | i = 1, \, 2, \, \ldots, \, n
| + | |
| - | </math>
| + | |
| - | , todas las ecuaciones del sistema se conviertan en identidades.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | [[Categoría:Matemáticas]]
| + | |
| - | | + | |
| - | %% }}}
| + | |
| - | %% {{{ =tipos de sistemas
| + | |
| - | <center>
| + | |
| - | [[Image:sistemas.gif|Clasificación de los sistemas de ecuaciones lineales]]
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Un sistema de ecuaciones es '''''compatible''''' cuando tiene solución.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Un sistema de ecuaciones es '''''compatible determinado''''' cuando tiene solución única.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Un sistema de ecuaciones es '''''compatible indeterminado''''' cuando tiene infinitas
| + | |
| - | soluciones.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Un sistema de ecuaciones es '''''incompatible''''' cuando no tiene solución.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Un sistema de ecuaciones es '''''homogéneo''''' cuando todos sus terminos independientes
| + | |
| - | son cero.
| + | |
| - | | + | |
| - | [[Category:Matemáticas]]
| + | |
| - | %% }}}
| + | |
| - | %% {{{ =método de reducción de Gauss
| + | |
| - | | + | |
| - | [[Imagen:gauss.jpg|frame|Gauss es uno de los matematicos mas
| + | |
| - | importantes de todos los tiempos. ¡Fue un GENIO!]]
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | El método de Gauss consiste en transformar el sistema dado en otro equivalente.
| + | |
| - | Para ello tomamos la [[Sistemas de ecuaciones lineales|matriz ampliada]] del
| + | |
| - | sistema y mediante las [[Matriz inversa#Operaciones elementales por filas en una matriz|operaciones elementales]]
| + | |
| - | por filas la transformamos en una matriz triangular superior ( o
| + | |
| - | inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil
| + | |
| - | de resolver.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | ==Ejemplo==
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | La matriz ampliada del sistema de ecuaciones:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left\{
| + | |
| - | \begin{array}[c]{ccc}
| + | |
| - | x \, + \, y \, + \, z & = & ~~3
| + | |
| - | \\
| + | |
| - | x \, + \, y \, - \, z & = & ~~1
| + | |
| - | \\
| + | |
| - | x \, - \, y \, - \, z & = & -1
| + | |
| - | \end{array}
| + | |
| - | \right.
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | es:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left(
| + | |
| - | \left.
| + | |
| - | \begin{array}[c]{ccc}
| + | |
| - | ~~1 & ~~1 & ~~1
| + | |
| - | \\
| + | |
| - | ~~1 & ~~1 & -1
| + | |
| - | \\
| + | |
| - | ~~1 & -1 & -1
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | ~~3
| + | |
| - | \\
| + | |
| - | ~~1
| + | |
| - | \\
| + | |
| - | -1
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Si a la tercera y segunda fila le restamos la primera, obtenemos:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left(
| + | |
| - | \left.
| + | |
| - | \begin{array}[c]{ccc}
| + | |
| - | ~~1 & ~~1 & ~~1
| + | |
| - | \\
| + | |
| - | ~~0 & ~~0 & -2
| + | |
| - | \\
| + | |
| - | ~~0 & -2 & -2
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | ~~3
| + | |
| - | \\
| + | |
| - | -2
| + | |
| - | \\
| + | |
| - | -4
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Si ahora intercambiamos la segunda y tercera filas, obtenemos
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left(
| + | |
| - | \left.
| + | |
| - | \begin{array}[c]{ccc}
| + | |
| - | ~~1 & ~~1 & ~~1
| + | |
| - | \\
| + | |
| - | ~~0 & -2 & -2
| + | |
| - | \\
| + | |
| - | ~~0 & ~~0 & -2
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | \begin{array}[c]{c}
| + | |
| - | ~~3
| + | |
| - | \\
| + | |
| - | -4
| + | |
| - | \\
| + | |
| - | -2
| + | |
| - | \end{array}
| + | |
| - | \right)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | que es la matriz ampliada del sistema de ecuaciones:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left\{
| + | |
| - | \begin{array}[c]{rcl}
| + | |
| - | x \, + \, y \, + \, z & = & ~~3
| + | |
| - | \\
| + | |
| - | -2y \, - \, 2z & = & -4
| + | |
| - | \\
| + | |
| - | -2z & = & -2
| + | |
| - | \end{array}
| + | |
| - | \right.
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | que es equivalente al inicial.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Solucionamos la tercera ocuacion para obtener
| + | |
| - | <math>
| + | |
| - | z
| + | |
| - | </math>
| + | |
| - | :
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | z \, = \, 1
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | En la primera y segunda ecuación, sustituimos
| + | |
| - | <math>
| + | |
| - | z
| + | |
| - | </math>
| + | |
| - | por la solucion de la tercera ecuación (
| + | |
| - | <math>
| + | |
| - | 1 \to z
| + | |
| - | </math>
| + | |
| - | ), para obtener:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left\{
| + | |
| - | \begin{array}[c]{rcl}
| + | |
| - | x \, + \, y \, + \, 1 & = & ~~3
| + | |
| - | \\
| + | |
| - | -2y \, - \, 2 & = & -4
| + | |
| - | \end{array}
| + | |
| - | \right.
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | La segunda ecuación es ahora una ecuación con una sola incognita,
| + | |
| - | <math>
| + | |
| - | y
| + | |
| - | </math>
| + | |
| - | . Que resolvemos para obtener
| + | |
| - | <math>
| + | |
| - | y \, = \, 1
| + | |
| - | </math>
| + | |
| - | . Sustituimos, en la primera ecuación,
| + | |
| - | <math>
| + | |
| - | y
| + | |
| - | </math>
| + | |
| - | por 1 (
| + | |
| - | <math>
| + | |
| - | 1 \to y
| + | |
| - | </math>
| + | |
| - | ). Esto nos da una ecuación en
| + | |
| - | <math>
| + | |
| - | x
| + | |
| - | </math>
| + | |
| - | :
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | x \, + \, 1 \, + \, 1 \, = \, 3
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | x \, = \, y \, = \, z \, = \, 1
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | [[Category:Matemáticas]]
| + | |
| - | | + | |
| - | %% }}}
| + | |
| - | %% {{{ =método de la matriz inversa
| + | |
| - | | + | |
| - | Un sistema de ecuaciones lineales se puede escribir en [[Sistemas de ecuaciones lineales|forma matricial]]:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | A \cdot X \, = \, B
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Si
| + | |
| - | <math>
| + | |
| - | A^{-1}
| + | |
| - | </math>
| + | |
| - | existe, es decir, si
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
| + | |
| - | la igualdad anterior por la izquierda por
| + | |
| - | <math>
| + | |
| - | A^{-1}
| + | |
| - | </math>
| + | |
| - | , para obtener:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | X \, = \, A^{-1} \cdot B
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | que es la solución del sistema de ecuaciones lineales de matriz de coeficientes
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | y matriz de terminos independientes
| + | |
| - | <math>
| + | |
| - | B
| + | |
| - | </math>
| + | |
| - | .
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | [[Category:Matemáticas]]
| + | |
| - | | + | |
| - | %% }}}
| + | |
| - | %% {{{ =regla de Cramer
| + | |
| - | | + | |
| - | [[Imagen:cramer2.gif|frame|Gabriel Cramer nacio Ginebra ( Suiza ) 1704 y murio en 1752. A
| + | |
| - | él le debemos la regla que lleva su nombre. ¡Gracias Gabriel por tu contribución a las Matemáticas!]]
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Esta regla es un metodo de resolución de sistemas de ecuaciones lineales que se puede
| + | |
| - | utilizar cuando la matriz
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | de coeficientes del sistema es cuadrada y de determinante no nulo. El que
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
| + | |
| - | coincide.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | Cuando el sistema de ecuaciones
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left.
| + | |
| - | \begin{array}{c}
| + | |
| - | a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1
| + | |
| - | \\
| + | |
| - | a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2
| + | |
| - | \\
| + | |
| - | \dotfill
| + | |
| - | \\
| + | |
| - | a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m
| + | |
| - | \end{array}
| + | |
| - | \right\}
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | satisface las condiciones arriba mencionadas, su solución viene dada por:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | x_1 \, = \, \frac
| + | |
| - | {
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cccc}
| + | |
| - | b_1 & a_{12} & \ldots & a_{1n}
| + | |
| - | \\
| + | |
| - | b_2 & a_{22} & \ldots & a_{2n}
| + | |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | b_m & a_{m2} & \ldots & a_{mn}
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | }
| + | |
| - | {|A|}
| + | |
| - | , \qquad \qquad x_2 \, = \, \frac
| + | |
| - | {
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cccc}
| + | |
| - | a_{11} & b_1 & \ldots & a_{1n}
| + | |
| - | \\
| + | |
| - | a_{21} & b_2 & \ldots & a_{2n}
| + | |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | a_{m1} & b_m & \ldots & a_{mn}
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | }
| + | |
| - | {|A|}, \qquad \qquad \ldots \ldots
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \ldots \ldots, \qquad \qquad x_n \, = \, \frac
| + | |
| - | {
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cccc}
| + | |
| - | a_{11} & a_{12} & \ldots & b_1
| + | |
| - | \\
| + | |
| - | a_{21} & a_{22} & \ldots & b_2
| + | |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | a_{m1} & a_{m2} & \ldots & b_m
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | }
| + | |
| - | {|A|}
| + | |
| - | \qquad \qquad
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | En general
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | x_i \, = \, \frac{|A_i|}{|A|}
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | donde
| + | |
| - | <math>
| + | |
| - | A_i
| + | |
| - | </math>
| + | |
| - | es la matriz que se obtiene sustituyendo la i-esima columna de
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | por la [[Sistemas de ecuaciones lineales|matriz de los terminos independientes]],
| + | |
| - | <math>
| + | |
| - | B
| + | |
| - | </math>
| + | |
| - | .
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | ==Ejemplo==
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | Consideremos el sistema de ecuaciones:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \left\{
| + | |
| - | \begin{array}[c]{rcl}
| + | |
| - | x \, + \, y \, = \, 2
| + | |
| - | \\
| + | |
| - | x \, - \, y \, = \, 0
| + | |
| - | \end{array}
| + | |
| - | \right.
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | En este sistema de ecuaciones lineales, la matriz
| + | |
| - | <math>
| + | |
| - | A
| + | |
| - | </math>
| + | |
| - | de los coeficientes es una matriz cuadrada y
| + | |
| - | <math>
| + | |
| - | |A| \, = \,
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cc}
| + | |
| - | 1 & ~~1
| + | |
| - | \\
| + | |
| - | 1 & -1
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | \, = \, -2 \neq 0
| + | |
| - | </math>
| + | |
| - | . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | x \, = \, \frac
| + | |
| - | {
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cc}
| + | |
| - | 2 & ~~1
| + | |
| - | \\
| + | |
| - | 0 & -1
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | }
| + | |
| - | {|A|} \, = \, \frac{-2}{-2} \, = \, 1
| + | |
| - | \qquad \qquad y \, = \, \frac
| + | |
| - | {
| + | |
| - | \left|
| + | |
| - | \begin{array}[c]{cc}
| + | |
| - | 1 & 2
| + | |
| - | \\
| + | |
| - | 1 & 0
| + | |
| - | \end{array}
| + | |
| - | \right|
| + | |
| - | }
| + | |
| - | {|A|}\, = \, \frac{-2}{-2} \, = \, 1
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | [[Category:Matemáticas]]
| + | |
| - | | + | |
| - | %% }}}
| + | |
| - | %% {{{ =teorema de Rouché-Frobenius
| + | |
| - | | + | |
| - | __TOC__
| + | |
| - | | + | |
| - | ==Enunciado==
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| | [[Imagen:frobenius.jpg|frame|Georg F. Fröbenius fue un matematico aleman que nacio en | | [[Imagen:frobenius.jpg|frame|Georg F. Fröbenius fue un matematico aleman que nacio en |
| | 1849 y murio en 1917. ¡Gracias Georg por tu legado!]] | | 1849 y murio en 1917. ¡Gracias Georg por tu legado!]] |
| | | | |
| - | <br/>
| + | ==Enunciado== |
| | | | |
| - | Un [[Sistemas de ecuaciones lineales|sistema]] de | + | {{teorema|1=Un [[Sistemas de ecuaciones lineales|sistema]] de |
| | <math> | | <math> |
| | m | | m |
| Línea 787: |
Línea 14: |
| | n | | n |
| | </math> | | </math> |
| - | incognitas es compatible ( tiene solución ) si, y sólo si, el [[Rango de una matriz|rango]] de la matriz de los coeficientes coincide con el rango de la matriz | + | incógnitas es compatible (tiene solución) si, y sólo si, el [[Rango de una matriz|rango]] de la matriz de los coeficientes coincide con el rango de la matriz |
| - | ampliada. | + | ampliada.|2=[[Rouche-Fröbenius]]}} |
| - | | + | |
| - | <br/>
| + | |
| | | | |
| | Si el sistema es compatible, existen dos posibilidades: | | Si el sistema es compatible, existen dos posibilidades: |
| | | | |
| - | <br/>
| + | # Que el rango de la matriz de los coeficientes sea menor que el numero de incógnitas. |
| - | | + | # Que el rango de la matriz de los coeficientes sea igual al numero de incognitas. |
| - | 1. Que el rango de la matriz de los coeficientes sea menor que el numero de incognitas.
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | 2. Que el rango de la matriz de los coeficientes sea igual al numero de incognitas.
| + | |
| - | | + | |
| - | <br/>
| + | |
| | | | |
| | En el primer caso el sistema es [[Tipos de sistemas de ecuaciones lineales|compatible | | En el primer caso el sistema es [[Tipos de sistemas de ecuaciones lineales|compatible |
| Línea 808: |
Línea 26: |
| | [[Tipos de sistemas de ecuaciones lineales|compatible determinado]]. | | [[Tipos de sistemas de ecuaciones lineales|compatible determinado]]. |
| | | | |
| - | <br/>
| |
| | | | |
| - | ==Ejemplo:sistemas homogeneos== | + | ==Ejemplo:sistemas homogéneos== |
| | | | |
| - | <br/>
| |
| | | | |
| - | En un sistema de ecuaciones homogeneo, la matriz | + | En un sistema de ecuaciones homogéneo, la columna de los términos independientes es nula, de manera que el |
| - | <math>
| + | |
| - | B
| + | |
| - | </math>
| + | |
| - | de los terminos independientes es una matriz nula, de manera que el
| + | |
| | [[Rango de una matriz|rango]] de la | | [[Rango de una matriz|rango]] de la |
| | [[Sistemas de ecuaciones lineales|matriz de los coeficientes]] y el de la | | [[Sistemas de ecuaciones lineales|matriz de los coeficientes]] y el de la |
| | [[Sistemas de ecuaciones lineales|matriz ampliada]] coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius, | | [[Sistemas de ecuaciones lineales|matriz ampliada]] coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius, |
| - | que un sistema homogeneo siempre es compatible. En cualquier sistema homogeneo, siempre | + | que un sistema homogéneo siempre es compatible. En cualquier sistema homogéneo, siempre |
| - | podemos obtener una solución particular igualando todas las incognitas a 0. | + | podemos obtener una solución particular -llamada solución trivial- igualando todas las incógnitas a 0. |
| - | | + | |
| - | <br/>
| + | |
| | | | |
| - | Un sistema homogeneo es compatible indeterminado cuando el determinante de la matriz de
| |
| - | los coeficientes es cero. Si este determinante no es cero el sistema homogeneo es
| |
| - | compatible determinado.
| |
| | | | |
| - | <br/>
| + | Un sistema homogéneo es compatible indeterminado cuando el número de incógnitas es mayor que el rango de la matriz de coeficientes. |
| | | | |
| | [[Category:Matemáticas]] | | [[Category:Matemáticas]] |



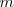 ecuaciones lineales con
ecuaciones lineales con
 incógnitas es compatible (tiene solución) si, y sólo si, el
incógnitas es compatible (tiene solución) si, y sólo si, el 
