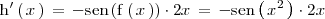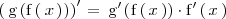Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Función derivada de la composición de funciones
De Wikillerato
(Diferencias entre revisiones)
(8 ediciones intermedias no se muestran.) Línea 1:
Línea 1: +
+ El componer dos funciones
<math>
<math>
\mathrm{f}
\mathrm{f}
</math>
</math>
- en el punto
+ y
<math>
<math>
- x \, = \, a
+ \mathrm{g}
</math>
</math>
- ,
+ consiste en aplicar
<math>
<math>
- \mathrm{f}^\prime
+ \mathrm{g }
- \left(
+
- \, a \,
+
- \right)
+
</math>
</math>
- , si existe, es el valor del limite:
+ al resultado de calcular
-
+
- <br/>
+
-
+
- <center>
+
<math>
<math>
- \lim_{h \to 0} \frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \,
+ \mathrm{f} \left( \, x \, \right)
- \mathrm{f} \left( \, a \, \right)}{h}
+
- </math>.
+
- </center>
+
-
+
- <br/>
+
-
+
- Si
+
- <math>
+
- \mathrm{f}^\prime
+
- \left(
+
- \, a \,
+
- \right)
+
- </math>
+
- es un número real, la función
+
- <math>
+
- \mathrm{f}
+
- </math>
+
- es derivable en
+
- <math>
+
- x \, = \, a
+
- </math>.
+
- Si
+
- <math>
+
- \mathrm{f}^\prime
+
- \left(
+
- \, a \,
+
- \right)
+
- </math>
+
- no es un número real o el límite no existe, la función
+
- <math>
+
- \mathrm{f}
+
- </math>
+
- no es derivable en dicho punto.
+
-
+
- <br/>
+
-
+
- ==Ejemplo==
+
-
+
- <br/>
+
-
+
- Calculemos la derivada de
+
- <math>
+
- \mathrm{f}
+
- \left(
+
- \, x \,
+
- \right)
+
- \, = \, x^2
+
- </math>
+
- en
+
- <math>
+
- x \, = \, 2
+
</math>:
</math>:
Línea 77:
Línea 21: <center>
<center>
<math>
<math>
- \mathrm{f}^\prime
+ x \longrightarrow \mathrm{f} \left( \, x \, \right) \longrightarrow \mathrm{g }
- \left(
+ \left( \mathrm{f} \left( \, x \, \right) \right)
- \, 2 \,
+
- \right)
+
- \, = \, \lim_{h \to 0} \frac{\mathrm{f}\left( \, 2 \, + \, h \, \right) \, - \,
+
- \mathrm{f} \left( \, 2 \, \right)}{h} \, = \, \lim_{h \to 0} \frac
+
- {\left( \, 2 \, + \, h \, \right)^2 \, - \, 2^2}{h} \, = \,
+
</math>
</math>
+ </center>
<br/>
<br/>
+ La [[Función derivada y derivadas sucesivas|derivada]] de
<math>
<math>
- \, = \, \lim_{h \to 0}
+ \mathrm {g } \left( \mathrm {f } \left( \, x \, \right) \right)
- \frac {\left( \, 4 \, + \, 4h \, + \, h^2 \, \right) \, - \, 4}{h} \, = \,
+
- \lim_{h \to 0} \frac {4h \, + \, h^2}{h} \, = \, \lim_{h \to 0}
+
- \left(
+
- \, h \, + 4 \, \,
+
- \right)
+
- \, = \, 4
+
</math>
</math>
- </center>
+ viene dada por la fórmula:
<br/>
<br/>
- [[Category:Matemáticas]]
+ <center>
- %% }}}
+ <math>
- %% {{{ =tasas de variación
+ \left(
-
+ \, \mathrm{g } \left( \mathrm{f } \left( \, x \, \right) \right)
- ==Tasa de variación media==
+ \right)
+ ^\prime \, = \, \mathrm {g}^\prime \left( \mathrm {f} \left( \, x \, \right) \right) \cdot \mathrm {f}^\prime \left( \, x \, \right)
+ </math>
+ </center>
<br/>
<br/>
- Supongamos que un coche de fórmula uno se mueve en una carretera totalmente recta. A
+ resultado que se conoce como '''''regla de la cadena'''''.
- distintas distancias de la salida se registran los tiempos de paso, obteniendose la
+
- siguiente tabla:
+
<br/>
<br/>
- <center>
+ ==Ejemplo==
- [[Imagen:tabla7.png]]
+
- </center>
+
<br/>
<br/>
- En este caso, la posición,
+ Calculemos la derivada de
- <math>
+
- y
+
- </math>
+
- , se puede ver como una función,
+
- <math>
+
- \mathrm{f}
+
- </math>
+
- , del tiempo,
+
- <math>
+
- x
+
- </math>; es decir:
+
<br/>
<br/>
Línea 138:
Línea 61: <center>
<center>
<math>
<math>
- y \, = \, \mathrm{f} \left( \, x \, \right)
+ \mathrm{h} \left( \, x \, \right) \, = \, \cos \left( \, x^2 \, \right)
</math>
</math>
</center>
</center>
Línea 144:
Línea 67: <br/>
<br/>
- La '''''tasa de variación media''''' de la posición en el intervalo de tiempo desde el
+
- instante
+
- <math>
+
- 9
+
- </math>
+
- al instante
+
<math>
<math>
- 13.4
+ \mathrm{h}
</math>
</math>
- es:
+ es la composición de dos funciones :
<br/>
<br/>
Línea 159:
Línea 77: <center>
<center>
<math>
<math>
- \frac{\mathrm{f} \left( \, 13.4 \, \right) \, - \, \mathrm{f} \left( \, 9 \,
+ \left\ {
- \right)}{13.4 \, - \, 9} \, = \, \frac{6.7 \, - \, 4.5}{13.4 \, - \, 9} \, = \, 0.5
+ \begin{array}[c]{rcl}
+ \mathrm{f} \left( \, x \, \right) \, & = & \, x^2
+ \\
+ \mathrm{g } \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
+ \end{array }
+ \right .
</math>
</math>
</center>
</center>
Línea 166:
Línea 89: <br/>
<br/>
- En general, la tasa de variación media de la función
+ Es decir
- <math>
+
- \mathrm{f}
+
- </math>
+
- en
+
- <math>
+
- \left[
+
- \, a, \, b \,
+
- \right]
+
- </math>
+
- se define como el cociente:
+
<br/>
<br/>
Línea 182:
Línea 95: <center>
<center>
<math>
<math>
- \frac{\mathrm{f} \left( \, b \, \right) \, - \, \mathrm{f} \left( \, a \,
+ \mathrm{h } \left( \, x \, \right) \, = \, \mathrm{g} \left( \, \mathrm{f} \left( \, x \, \right) \right)
- \right)}{b \, - \, a}
+
</math>
</math>
</center>
</center>
Línea 189:
Línea 101: <br/>
<br/>
- ==Tasa de variación instantánea==
+ Para derivar
-
+
- <br/>
+
-
+
- La '''''tasa de variación instantánea''''' de la función
+
<math>
<math>
- f
+ \mathrm{h} \left( \, x \, \right)
</math>
</math>
- en el punto
+ utilizamos la regla de la cadena:
- <math>
+
- x \, = \, a
+
- </math>
+
- se obtiene haciendo tender
+
- <math>
+
- b
+
- </math>
+
- a
+
- <math>
+
- a
+
- </math>
+
- en la '''''tasa de variación media''''' de la función
+
- <math>
+
- f
+
- </math>
+
- en el intervalo
+
- <math>
+
- \left[
+
- \, a, \, b \,
+
- \right]
+
- </math>; por tanto, la '''''tasa de variación instantánea''''' de la función
+
- <math>
+
- f
+
- </math>
+
- en el punto
+
- <math>
+
- x \, = \, a
+
- </math>
+
- es
+
<br/>
<br/>
Línea 232:
Línea 111: <center>
<center>
<math>
<math>
- \lim_{h \to 0}\frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, \mathrm{f}\left( \, a \, \right)}{h}
+ \mathrm {h}^ \prime \left( \, x \, \right) \, = \, \mathrm{g }^\prime \left( \, \mathrm{f} \left( \, x \, \right) \right) \cdot \mathrm{f}^\prime \left( \, x \, \right)
</math>
</math>
</center>
</center>
Línea 238:
Línea 117: <br/>
<br/>
- que es precisamente la [[Definición de derivada|derivada]] de la función
+ Como
- <math>
+
- f
+
- </math>
+
- en el punto
+
- <math>
+
- x \, = \, a
+
- </math>.
+
<br/>
<br/>
-
- NOTA: En el límite anterior
- <math>
- b \, = \, a \, + \, h
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =Derivadas de las funciones elementales
<center>
<center>
- [[Imagen:tablaDeDerivadas.png]]
- </center>
-
- %% }}}
- %% {{{ =función derivada
-
- Si
<math>
<math>
- \mathrm{f}
+ \left\{
+ \begin{array}[c]{rcl}
+ \mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
+ \\
+ \mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
+ \end{array}
+ \right.
</math>
</math>
- es una función derivable en el intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- \subset R
- </math>
- , la '''''función derivada''''' de
- <math>
- \mathrm{f}
- </math>
- es la que a cada
- <math>
- x \in
- \left(
- \, a, \, b \,
- \right)
- </math>
- le hace corresponder la [[Definición de derivada|derivada]] de
- <math>
- \mathrm{f}
- </math>
- en dicho punto. Esta función se designa por
- <math>
- \mathrm{f}^\prime \left( \, x \, \right)
- </math>.
-
- <br/>
-
- Una función
- <math>
- \mathrm{f}
- </math>
- es '''''derivable''''' en el intervalo
- <math>
- \left(
- \, a, \, b \,
- \right)
- </math>
- si lo es en cada punto del intervalo.
-
- <br/>
-
- Llamamos '''''derivada de segundo orden''''' de
- <math>
- \mathrm{f}
- </math>
- a la función derivada de
- <math>
- \mathrm{f}^\prime
- </math>.
- Esta función se denota por
- <math>
- \mathrm{f}^{\prime \prime}
- </math>.
-
- <br/>
-
- <math>
- \mathrm{f}^{\prime \prime \prime}
- </math>
- es la '''''derivada tercera''''' de
- <math>
- \mathrm{f}
- </math>
- y, en general,
- <math>
- \mathrm{f}^{\left( \, n \, \right)}
- </math>
- es la '''''derivada n-ésima''''' de
- <math>
- \mathrm{f} \left( \, x \, \right)
- </math>:
- <math>
- \mathrm{f}^{\left( \, n \, \right)}
- </math>
- es la función derivada de
- <math>
- \mathrm{f}^{\left( \, n \, - \, 1 \, \right)}
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =significado geométrico de la derivada
-
- Consideremos la grafica de una función
- <math>
- \mathrm{f}
- </math>
- . Tomemos un punto
- <math>
- A \, = \,
- \left(
- \, A_x, \, \mathrm{f} \left( \, A_x \, \right) \,
- \right)
- </math>
- en dicha grafica y consideremos una sucesión de puntos
- <math>
- A_1, \, A_2, \, A_3, \, \ldots
- </math>
- en la grafica de
- <math>
- \mathrm{f}
- </math>
- . Supongamos que todos estos puntos estan a la derecha de
- <math>
- A
- </math>
- y que cuando
- <math>
- n \to \infty
- </math>
- ,
- <math>
- A_n \to A
- </math>.
-
- <br/>
-
- La recta que pasa por los puntos
- <math>
- A
- </math>
- y
- <math>
- A_n
- </math>
- es una secante a la grafica de la función
- <math>
- \mathrm{f}
- </math>. De esta forma, hay una secante para cada punto
- <math>
- A_n
- </math>. Sea
- <math>
- s_n
- </math>
- la recta que pasa por
- <math>
- A
- </math>
- y por
- <math>
- A_n
- </math>
- .
-
- <br/>
-
- <center>
- [[Imagen:tangente.png]]
</center>
</center>
<br/>
<br/>
- Cuando
+ se tiene que
- <math>
+
- n
+
- </math>
+
- tiende a
+
- <math>
+
- \infty
+
- </math>
+
- ,
+
- <math>
+
- s_n
+
- </math>
+
- tiende a la tangente a la grafica de la función
+
- <math>
+
- \mathrm{f}
+
- </math>
+
- en el punto
+
- <math>
+
- A
+
- </math>,
+
- <math>
+
- t
+
- </math>:
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- s_n \to t
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- Habria de esperar, pues, que la pendiente de
+
- <math>
+
- s_n
+
- </math>
+
- tienda a la pendiente de
+
- <math>
+
- t
+
- </math>
+
- cuando
+
- <math>
+
- n
+
- </math>
+
- tiende a
+
- <math>
+
- \infty
+
- </math>. Como la pendiente de
+
- <math>
+
- s_n
+
- </math>
+
- es una [[La derivada como una tasa de variación instantánea|tasa de variación
+
- media]]:
+
<br/>
<br/>
Línea 490:
Línea 141: <center>
<center>
<math>
<math>
- \frac{\mathrm{f} \left( \, A_{n,x} \, \right) \, - \, \mathrm{f} \left( \, A_x \,
+ \mathrm{h }^\prime \left( \, x \, \right) \, = \, -\mathrm{sen} \left(
- \right)}{A_{n,x} \, - \, A_x}
+ \mathrm{f} \left( \, x \, \right) \right) \cdot 2x \ , = \, -\mathrm{sen } \left(
+ \, x^2 \, \right) \cdot 2x
</math>
</math>
-
- <br/>
-
- (<math>
- A_{n,x} \, =
- </math>
- abcisa de
- <math>
- A_n
- </math>)
</center>
</center>
-
- <br/>
-
- su limite cuando
- <math>
- n \to \infty
- </math>
- es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de
- <math>
- \mathrm{f}
- </math>
- en
- <math>
- A_x
- </math>; es decir la pendiente de
- <math>
- t
- </math>
- es la derivada de
- <math>
- \mathrm{f}
- </math>
- en
- <math>
- A_x
- </math>.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =función derivada de las operaciones de funciones
-
- __TOC__
-
- <br/>
-
- ==Derivada de la suma==
-
- <br/>
-
- La [[Función derivada y derivadas sucesivas|derivada]] de la suma de dos funciones es
- igual a la suma de las derivadas de dichas funciones:
-
- <br/>
-
- <center>
- <math>
- \left(
- \, \mathrm{f} \, + \, \mathrm{g} \,
- \right)
- ^\prime \, = \, \mathrm{f}^\prime \, + \, \mathrm{g}^\prime \,
- </math>
- </center>
-
- <br/>
-
- Este resultado, se puede ampliar a cualquier número de funciones.
-
- <br/>
-
- ==Derivada de la diferencia==
-
- <br/>
-
- La [[Función derivada y derivadas sucesivas|derivada]] de la diferencia de dos funciones es
- igual a la diferencia de las derivadas de dichas funciones:
-
- <br/>
-
- <center>
- <math>
- \left(
- \, \mathrm{f} \, - \, \mathrm{g} \,
- \right)
- ^\prime \, = \, \mathrm{f}^\prime \, - \, \mathrm{g}^\prime \,
- </math>
- </center>
-
- <br/>
-
- ==Derivada del producto==
-
- <br/>
-
- La [[Función derivada y derivadas sucesivas|derivada]] del producto de dos funciones,
-
- <math>
- \mathrm{f}
- </math>
- y
- <math>
- \mathrm{g}
- </math>
- , viene dada por la fórmula:
-
- <br/>
-
- <center>
- <math>
- \left(
- \, \mathrm{f} \cdot \mathrm{g} \,
- \right)
- ^\prime \, = \, \mathrm{f}^\prime \cdot \mathrm{g} \, + \, \mathrm{f} \cdot \mathrm{g}^\prime \,
- </math>
- </center>
-
- <br/>
-
- ==Derivada del cociente==
-
- <br/>
-
- La [[Función derivada y derivadas sucesivas|derivada]] del cociente
- <math>
- \frac{f}{g}
- </math>
- viene dada por la fórmula:
-
- <br/>
-
- <center>
- <math>
- \left(
- \, \frac{f}{g} \,
- \right)
- ^\prime \, = \, \frac{\mathrm{f}^\prime \cdot \mathrm{g} \, - \, \mathrm{f} \cdot \mathrm{g}^\prime}{\mathrm{g}^2}
- </math>
- </center>
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =composición de funciones
-
- El componer dos funciones
- <math>
- \mathrm{f}
- </math>
- y
- <math>
- \mathrm{g}
- </math>
- consiste en aplicar
- <math>
- g
- </math>
- al resultado de calcular
- <math>
- \mathrm{f} \left( \, x \, \right)
- </math>
- , es decir:
-
- <br/>
-
- <center>
- <math>
- R \stack{\mathrm{f}}{\longrightarrow} R \stack{\mathrm{g}}{\longrightarrow} R
- </math>
-
- <br/>
-
- <math>
- x \longrightarrow \mathrm{f} \left( \, x \, \right) \longrightarrow \mathrm{g}
- \left( \mathrm{f} \left( \, x \, \right) \right)
- </math>
-
- </center>
-
- <br/>
-
- La [[Función derivada y derivadas sucesivas|derivada]] de
- <math>
- \mathrm{g} \left( \mathrm{f} \left( \, x \, \right) \right)
- </math>
- viene dada por la fórmula:
-
- <br/>
-
- <center>
- <math>
- \mathrm{g}^\prime \left( \mathrm{f} \left( \, x \, \right) \right) \cdot \mathrm{f}^\prime \left( \, x \, \right)
- </math>
- </center>
-
- <br/>
-
- resultado que se conoce como '''''regla de la cadena'''''.
<br/>
<br/>
[[Category:Matemáticas]]
[[Category:Matemáticas]]
Revisión actual
El componer dos funciones
La derivada de
resultado que se conoce como regla de la cadena
Ejemplo
Calculemos la derivada de
Es decir
Para derivar
Como
se tiene que
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
 y
y
 consiste en aplicar
consiste en aplicar
 al resultado de calcular
al resultado de calcular
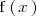 :
:
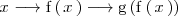
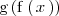 viene dada por la fórmula:
viene dada por la fórmula:
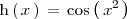
 es la composición de dos funciones:
es la composición de dos funciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f} \left( \, x \, \right) \, & = & \, x^2
\\
\mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f} \left( \, x \, \right) \, & = & \, x^2
\\
\mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
\end{array}
</pre>
<p>\right.](/images/math/math-693d66707eee4ea00c554a821a1e1902.png)
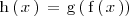
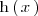 utilizamos la regla de la cadena:
utilizamos la regla de la cadena:
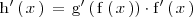
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
\\
\mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
\\
\mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
\end{array}
</pre>
<p>\right.](/images/math/math-87d2e3c97615febe5a00ed62cd9f55bb.png)