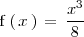Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Simetrías

De Wikillerato

(Diferencias entre revisiones)
Revisión actual (17:53 26 mar 2008) (editar) (deshacer)
(→Ejemplo)
 
(3 ediciones intermedias no se muestran.)
Línea 15: Línea 15:
<br/>
<br/>
-
Si una función es '''''par''''', su grafica presenta una simetría respecto al eje de
+
Si una función es '''''par''''', su gráfica presenta una simetría respecto al eje de
ordenadas.
ordenadas.
Línea 52: Línea 52:
<br/>
<br/>
-
Si una función es '''''impar''''', su grafica presenta una simetría respecto al eje de
+
Si una función es '''''impar''''', su gráfica presenta una simetría respecto al origen de
-
ordenadas.
+
coordenadas.
<br/>
<br/>

Revisión actual

Tabla de contenidos

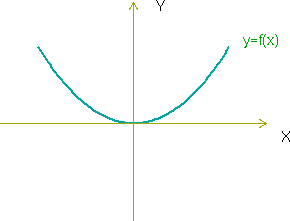
Función par


Una función es par si se cumple que:


\mathrm{f} \left( \, -x \, \right) \, = \, \mathrm{f} \left( \, x \, \right)


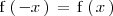
Si una función es par, su gráfica presenta una simetría respecto al eje de ordenadas.


Ejemplo


\mathrm{f} \left( \, x \, \right) \, = \, \frac{x^2}{4}


Imagen:funcion2.png


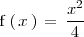
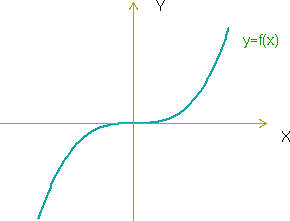
Función impar


Una función es impar si se cumple que:


\mathrm{f} \left( \, -x \, \right) \, = \, -\mathrm{f} \left( \, x \, \right)


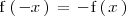
Si una función es impar, su gráfica presenta una simetría respecto al origen de coordenadas.


Ejemplo


\mathrm{f} \left( \, x \, \right) \, = \, \frac{x^3}{8}


Imagen:funcion3.png


Obtenido de "http://wikillerato.org/Simetr%C3%ADas.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.