Energía e intensidad de las ondas
De Wikillerato
| (17 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
Se han definido las ondas como un fenómeno de transmisión de energía sin que haya transporte de materia ¿Ahora bien, cuál es la energía que se propaga? Es evidente que la que contiene el foco emisor. Si nos atenemos a alguno de los ejemplos sencillos que se han descrito, ondas sobre una cuerda, sobre la superficie del agua, en ambos casos será la energía del oscilador, siendo la energía del oscilador igual a la '''energía potencial elástica''' que será | Se han definido las ondas como un fenómeno de transmisión de energía sin que haya transporte de materia ¿Ahora bien, cuál es la energía que se propaga? Es evidente que la que contiene el foco emisor. Si nos atenemos a alguno de los ejemplos sencillos que se han descrito, ondas sobre una cuerda, sobre la superficie del agua, en ambos casos será la energía del oscilador, siendo la energía del oscilador igual a la '''energía potencial elástica''' que será | ||
| - | <math> E = \frac {1}{2}k \mbox{ } A^2 = \frac {1}{2} | + | <math> E = \frac {1}{2}k \mbox{ } A^2 = \frac {1}{2}m {v_{max}}^2</math> |
De tal modo que cuando la masa del punto M que hemos considerado en las ondas, alcanza la '''elongación máxima''' <math>y_{max} = A</math>, es decir igual a la amplitud, toda su energía será potencial, y cuando pase por las posiciones <math>y = 0</math> toda su energía será cinética, es decir, pasará a la velocidad máxima. | De tal modo que cuando la masa del punto M que hemos considerado en las ondas, alcanza la '''elongación máxima''' <math>y_{max} = A</math>, es decir igual a la amplitud, toda su energía será potencial, y cuando pase por las posiciones <math>y = 0</math> toda su energía será cinética, es decir, pasará a la velocidad máxima. | ||
| Línea 7: | Línea 7: | ||
Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda | Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda | ||
| - | <math> v = \frac{dy}{dt} = \frac{d | + | <math> v = \frac{dy} {dt} = \frac{d (A \mbox { } sen ( \omega t- k x))}{dt} = \omega A \mbox { } cos ( \omega t - kz)</math> |
Dado que el valor máximo de un cos es 1, la velocidad máxima será <math>v = \omega A</math> | Dado que el valor máximo de un cos es 1, la velocidad máxima será <math>v = \omega A</math> | ||
| - | <math> E = \frac{1}{2}m \omega^2 A^2 = \frac{1}{2}m (2 \pi f)^2 A^2</math> | + | <math> E = \frac {1} {2} m \mbox { } \omega^2 A^2 = \frac{1}{2}m (2 \pi f)^2 A^2</math> |
De dónde obtenemos que la energía total que se transmite es: | De dónde obtenemos que la energía total que se transmite es: | ||
| - | <math> E = | + | <math> E = 2 \pi^2 m A^2 f^2 </math> o también |
| - | <math> E = \frac{1}{2}m \omega^2 A^2</math> | + | <math> E = \frac {1} {2} m \mbox{ } \omega ^ 2 A ^ 2 </math> |
| + | |||
| + | Vemos que la '''energía es proporcional al cuadrado de la amplitud y al cuadrado de la frecuencia'''. | ||
| + | |||
| + | En una cuerda en la que se propage una onda sin amortiguamiento, la amplitud se mantiene constante. Esto es debido a que la onda es unidimensional. | ||
| + | |||
| + | Sin embargo, si estudiamos la amplitud de un pulso en la superficie del agua, observamos que va disminuyendo a medida que el círculo que se forma va teniendo un radio mayor, es decir, a medida que se aleja del foco emisor. | ||
| + | |||
| + | Si nos alejamos de una fuente sonora, oiremos el sonido cada vez más apagado. La variación de presión que se produce en la fuente sonora se tiene que repartir entre todos los puntos de la superficie de las esferas concéntricas que van recibiendo las variaciones de presión del medio. Llega un momento en que nuestro oído no pèrcibe las señales sonoras que nos llegan. Un lobo si la oiría aún. | ||
| + | |||
| + | La percepción de una farola situada en un punto en el campo va disminuyendo hasta que nuestro ojo ya no es capaz de percibir los fotones que le llegan desde esa farola. El número de fotones que parten de la farola es constante, pero deben repartirse entre todos los puntos de superficies esféricas en las cuales nos encontramos. Si nos alejamos, el número de fotones percibidos por nuestro ojo va siendo cada vez menor, hasta que nuestro ojo no percibe la señal luminosa | ||
| + | . | ||
| + | Sin embargo no debemos confundir la disminución de la amplitud debida a la razón expuesta, con el amortiguamiento que se observa en ocasiones debido a que la energía mecánica se degrada en forma de calor cuando se propaga en medios elásticos. | ||
| + | |||
| + | Pero veamos la primera razón de la disminución de la amplitud A cuando la onda se propaga, pues ya hemos considerado que no hay amortiguamiento de las ondas. | ||
| + | |||
| + | La disminución de la amplitud se producirá siempre que la onda es bi o tridimensional. Como nuestra percepción también depende de la potencia del foco emisor, tendremos. | ||
| + | |||
| + | <math> P = \frac{W}{t}\ = \frac {2 \pi^2 m A^2 f^2}{t}</math> | ||
| + | |||
| + | Si la onda se propaga en la superficie del agua, esa energía se tendrá que repartir entre todos los puntos que son alcanzados por el pulso al mismo tiempo, es decir la longitud de las circunferencias que van formándose con un radio cada vez mayor. Todos los puntos de esas circunferencias están vibrando en concordancia de fase puesto que la distancia al foco emisor será la misma, es decir, el radio r de cada circunferencia.r. | ||
| + | Dado que la velocidad de propagación de las ondas en cada punto es perpendicular al frente de ondas formado | ||
| + | |||
| + | La potencia en un punto será pues: | ||
| + | |||
| + | |||
| + | <math> P = \frac {W} {2 \pi rt}</math> | ||
| + | |||
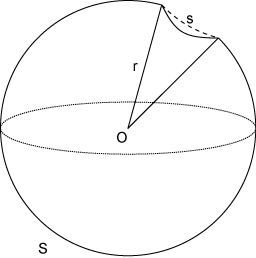
| + | En el caso del sonido, si éste se propaga en un medio homogéneo y isotrópico, la onda formada es tridimensional, la energía del foco emisor se distribuye entre todos los puntos de la superficie de la onda que, por tratarse de esferas concéntricas con el foco emisor, será <math>S = 4 \pi r^2</math>. | ||
| + | |||
| + | Para determinar la potencia en un punto del medio escribiremos: | ||
| + | |||
| + | <math> P = \frac {W} {4\pi r^2 t}</math> | ||
| + | |||
| + | Si nos encontramos en un punto que nos determina un elemento de superficie s, la energía que llega a ese elemento de superficie será: | ||
| + | |||
| + | [[Imagen:Ondaenergia.png]] | ||
| + | |||
| + | <br /> | ||
| + | <math> w= W \frac{s} {S}</math> | ||
| + | |||
| + | Llamamos '''Intensidad I de una onda a la energía que atraviesa por unidad de tiempo y por unidad de superficie perpendicular a la dirección de propagación de la onda'''. | ||
| + | |||
| + | <math> I = \frac { \frac{W}{t}} {S}</math> dado que <math> P = \frac{W}{t}</math> | ||
| + | |||
| + | Tendremos que <math>I = \frac {P} {S}</math> | ||
| + | |||
| + | Así como la '''energía se mide en julios <math>J</math> y la potencias en vatios <math>W</math>, la intensidad se mide en <math>J s^{-1} m^{-2}</math> o también en''' <math>W m^{-2}</math>. Si se trata de encontrar la potencia en un elemento de superficie <math>s</math>, tendremos: | ||
| + | |||
| + | <math> p = P \frac {s} {S}</math> | ||
| + | |||
| + | Por eso se utiliza el megáfono o se juntan las manos alrededor de la boca, pues ello permite que se pierda la menor cantidad de energía por la parte exterior de la boca de salida.. | ||
| + | |||
| + | Pero lo mismo ocurrirá con la intensidad. Si comparamos la relación que existe entre la intensidad entre dos frentes situados a las distancia <math>r_1</math> y <math>r_2</math>, encontraremos: | ||
| + | |||
| + | <math> I_1= \frac {W} {4 \pi (r_1)^2 t} </math> | ||
| + | |||
| + | <math> I_2= \frac{W}{4 \pi (r_2)^2 t} </math> | ||
| + | |||
| + | <math> \frac { I_1} { I_2} = \frac{(r_2)^2}{(r_1)^2} </math> | ||
| + | |||
| + | Vemos pues que la intensidad que llega los puntos de un medio trimensional es inversamente proporcional al cuadrado de las distancias al foco emisor. | ||
| + | |||
| + | También se puede escribir: | ||
| + | |||
| + | <math> \frac{ I_1}{ I_2}\ = \frac {(A_1)^2}{(A_2)^2} </math> | ||
| + | |||
| + | O también: | ||
| + | |||
| + | <math> \frac{ A_1}{ A_2}\ = \frac {r_2}{r_1} </math> | ||
| + | |||
| + | La amplitud de la onda es inversamente proporcional a la distancia a la fuente de las perturbaciones. | ||
| + | |||
| + | En el sonido, como ya se verá, la energía emitida por segundo por el foco emisor es su '''potencia <math>P</math>, es una magnitud física, y la intensidad, tal como se ha definido también''', tanto que len el sonido hay lo que definimos como '''intensidad fisiológica''' que es una cualidad fisiológica la cual se abordará al estudiar el sonido. | ||
| + | |||
| + | [[Categoría:Física]] | ||
Revisión actual
Se han definido las ondas como un fenómeno de transmisión de energía sin que haya transporte de materia ¿Ahora bien, cuál es la energía que se propaga? Es evidente que la que contiene el foco emisor. Si nos atenemos a alguno de los ejemplos sencillos que se han descrito, ondas sobre una cuerda, sobre la superficie del agua, en ambos casos será la energía del oscilador, siendo la energía del oscilador igual a la energía potencial elástica que será
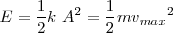
De tal modo que cuando la masa del punto M que hemos considerado en las ondas, alcanza la elongación máxima 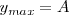 , es decir igual a la amplitud, toda su energía será potencial, y cuando pase por las posiciones
, es decir igual a la amplitud, toda su energía será potencial, y cuando pase por las posiciones 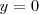 toda su energía será cinética, es decir, pasará a la velocidad máxima.
toda su energía será cinética, es decir, pasará a la velocidad máxima.
Pero si queremos determinar el valor de la velocidad en cualquier punto habremos de derivar con relación al tiempo la elongación, es decir, la ecuación de la onda
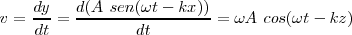
Dado que el valor máximo de un cos es 1, la velocidad máxima será 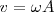
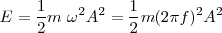
De dónde obtenemos que la energía total que se transmite es:
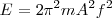 o también
o también
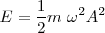
Vemos que la energía es proporcional al cuadrado de la amplitud y al cuadrado de la frecuencia.
En una cuerda en la que se propage una onda sin amortiguamiento, la amplitud se mantiene constante. Esto es debido a que la onda es unidimensional.
Sin embargo, si estudiamos la amplitud de un pulso en la superficie del agua, observamos que va disminuyendo a medida que el círculo que se forma va teniendo un radio mayor, es decir, a medida que se aleja del foco emisor.
Si nos alejamos de una fuente sonora, oiremos el sonido cada vez más apagado. La variación de presión que se produce en la fuente sonora se tiene que repartir entre todos los puntos de la superficie de las esferas concéntricas que van recibiendo las variaciones de presión del medio. Llega un momento en que nuestro oído no pèrcibe las señales sonoras que nos llegan. Un lobo si la oiría aún.
La percepción de una farola situada en un punto en el campo va disminuyendo hasta que nuestro ojo ya no es capaz de percibir los fotones que le llegan desde esa farola. El número de fotones que parten de la farola es constante, pero deben repartirse entre todos los puntos de superficies esféricas en las cuales nos encontramos. Si nos alejamos, el número de fotones percibidos por nuestro ojo va siendo cada vez menor, hasta que nuestro ojo no percibe la señal luminosa . Sin embargo no debemos confundir la disminución de la amplitud debida a la razón expuesta, con el amortiguamiento que se observa en ocasiones debido a que la energía mecánica se degrada en forma de calor cuando se propaga en medios elásticos.
Pero veamos la primera razón de la disminución de la amplitud A cuando la onda se propaga, pues ya hemos considerado que no hay amortiguamiento de las ondas.
La disminución de la amplitud se producirá siempre que la onda es bi o tridimensional. Como nuestra percepción también depende de la potencia del foco emisor, tendremos.
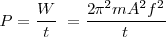
Si la onda se propaga en la superficie del agua, esa energía se tendrá que repartir entre todos los puntos que son alcanzados por el pulso al mismo tiempo, es decir la longitud de las circunferencias que van formándose con un radio cada vez mayor. Todos los puntos de esas circunferencias están vibrando en concordancia de fase puesto que la distancia al foco emisor será la misma, es decir, el radio r de cada circunferencia.r. Dado que la velocidad de propagación de las ondas en cada punto es perpendicular al frente de ondas formado
La potencia en un punto será pues:
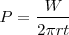
En el caso del sonido, si éste se propaga en un medio homogéneo y isotrópico, la onda formada es tridimensional, la energía del foco emisor se distribuye entre todos los puntos de la superficie de la onda que, por tratarse de esferas concéntricas con el foco emisor, será 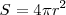 .
.
Para determinar la potencia en un punto del medio escribiremos:
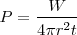
Si nos encontramos en un punto que nos determina un elemento de superficie s, la energía que llega a ese elemento de superficie será:
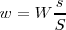
Llamamos Intensidad I de una onda a la energía que atraviesa por unidad de tiempo y por unidad de superficie perpendicular a la dirección de propagación de la onda.
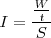 dado que
dado que 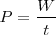
Tendremos que 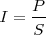
Así como la energía se mide en julios 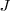 y la potencias en vatios
y la potencias en vatios 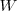 , la intensidad se mide en
, la intensidad se mide en 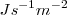 o también en
o también en 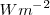 . Si se trata de encontrar la potencia en un elemento de superficie
. Si se trata de encontrar la potencia en un elemento de superficie  , tendremos:
, tendremos:
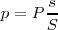
Por eso se utiliza el megáfono o se juntan las manos alrededor de la boca, pues ello permite que se pierda la menor cantidad de energía por la parte exterior de la boca de salida..
Pero lo mismo ocurrirá con la intensidad. Si comparamos la relación que existe entre la intensidad entre dos frentes situados a las distancia 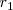 y
y 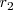 , encontraremos:
, encontraremos:
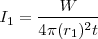
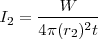
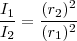
Vemos pues que la intensidad que llega los puntos de un medio trimensional es inversamente proporcional al cuadrado de las distancias al foco emisor.
También se puede escribir:
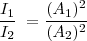
O también:
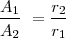
La amplitud de la onda es inversamente proporcional a la distancia a la fuente de las perturbaciones.
En el sonido, como ya se verá, la energía emitida por segundo por el foco emisor es su potencia  , es una magnitud física, y la intensidad, tal como se ha definido también, tanto que len el sonido hay lo que definimos como intensidad fisiológica que es una cualidad fisiológica la cual se abordará al estudiar el sonido.
, es una magnitud física, y la intensidad, tal como se ha definido también, tanto que len el sonido hay lo que definimos como intensidad fisiológica que es una cualidad fisiológica la cual se abordará al estudiar el sonido.