Fuerzas y Sistemas Materiales
De Wikillerato
(→Interacciones mecánicas) |
m (Revertidas las ediciones realizadas por 190.41.176.53 (Talk); a la última edición de Laura.2mdc) |
||
| (28 ediciones intermedias no se muestran.) | |||
| Línea 9: | Línea 9: | ||
| - | + | [[Imagen:Tension1.jpg]] | |
Si queremos estudiar las interacciones de un modelo separado '''aislamos''' la parte del sistema a estudiar, como se señala con las líneas roja y azul, respectivamente. En los extremos del hilo tendremos <math>\vec F = - \vec T \ y \vec \ T = - \vec P</math>. | Si queremos estudiar las interacciones de un modelo separado '''aislamos''' la parte del sistema a estudiar, como se señala con las líneas roja y azul, respectivamente. En los extremos del hilo tendremos <math>\vec F = - \vec T \ y \vec \ T = - \vec P</math>. | ||
| Línea 20: | Línea 20: | ||
| - | + | [[Imagen:Tension2.jpg]] | |
| Línea 28: | Línea 28: | ||
El cilindro ejerce una acción sobre la mesa igual a su peso <math>\vec P = m \vec g</math>, que es vertical. El tablero debe ejercer una fuerza igual de sentido contrario, '''Fuerza de Reacción, R,''' perpendicular al plano de la mesa, que se encontrará distribuida entre todos los puntos de la base del cilindro. | El cilindro ejerce una acción sobre la mesa igual a su peso <math>\vec P = m \vec g</math>, que es vertical. El tablero debe ejercer una fuerza igual de sentido contrario, '''Fuerza de Reacción, R,''' perpendicular al plano de la mesa, que se encontrará distribuida entre todos los puntos de la base del cilindro. | ||
| - | + | [[Imagen:Tension3.jpg]] | |
| Línea 38: | Línea 38: | ||
La Tierra atrae a la Luna con una '''acción''' tal que sólo, y nada menos, puede hacer variar la dirección de su movimiento, obligándola a evolucionar alrededor de la Tierra. La Luna ejerce una fuerza igual y de signo contrario sobre la Tierra, pero la masa de la tierra es muy grande para desviar su trayectoria, sin embargo, como se verá, sí que influye sobre la altura de las mareas. | La Tierra atrae a la Luna con una '''acción''' tal que sólo, y nada menos, puede hacer variar la dirección de su movimiento, obligándola a evolucionar alrededor de la Tierra. La Luna ejerce una fuerza igual y de signo contrario sobre la Tierra, pero la masa de la tierra es muy grande para desviar su trayectoria, sin embargo, como se verá, sí que influye sobre la altura de las mareas. | ||
| + | |||
| + | |||
| + | [[Imagen:Tension4.jpg]] | ||
| + | |||
| + | |||
| + | La '''acción que ejerce la Tierra sobre la Luna,''' <math>\vec F_{T,L}</math>, es igual y de sentido opuesto a la reacción de la Luna sobre la tierra, <math>\vec F_{L,T}</math> Ambas fuerzas se encuentran aplicadas sobre el centro de la Luna y de la Tierra, respectivamente, y su dirección es la de la línea que los une. | ||
| + | |||
| + | Del mismo modo podemos plantear la existencia de dos fuerzas iguales y de sentido opuesto cuando se trata de fuerzas eléctricas que son también fuerzas a distancia. | ||
| + | |||
| + | |||
| + | ===Principio de Acciones Recíprocas o Principio de Acción y Reacción=== | ||
| + | |||
| + | Es de todo punto evidente que para existir, una fuerza debe ser ejercida por algo o alguien sobre otro cuerpo. Del mismo modo, un cuerpo no puede ser empujado (o arrastrado) si no hay al menos algo que lo empuje o lo arrastre. '''''Es decir, podemos afirmar que en la naturaleza las fuerzas existen a pares de tal modo que una se opone a la otra.''''' No hay fuerzas aisladas, sólo existen interacciones entre los cuerpos, y el problema radica en saber quien empuja y quien es empujado, o quien tira y quien es arrastrado. | ||
| + | |||
| + | |||
| + | Siempre que en el sistema estudiado aparece un organismo vivo, hay una tendencia a creer que es él el que ejerce la acción. En la mina, siempre imaginamos al minero empujando la vagoneta y no al revés. Sin embargo, esta creencia desaparece cuando se trata de dos objetos inanimados. | ||
| + | |||
| + | Si en el mercado nos pesan un kilogramo de carne sobre una balanza de torsión, llegamos sin dificultad a la conclusión de que la carne ejerce una acción sobre el plato de la balanza, y que éste ejerce sobre la carne una fuerza igual y de signo opuesto. | ||
| + | Newton, enunció lo que hoy llamamos 3ª Ley de Newton o Principio de acción y reacción, '''''“A toda acción le corresponde una reacción de igual intensidad y sentido contrario”.''''' | ||
| + | |||
| + | Este enunciado parece que privilegia una de las fuerzas, la acción, sobre la otra, la de reacción, cuando ambas fuerzas ejercen el mismo papel en el estado del sistema material estudiado, y que no puede existir la una sin la otra. Por eso hoy este principio queda mejor expresado de otra forma: | ||
| + | |||
| + | '''''“Si dos sólidos S1 y S2 se encuentran en interacción mecánica, la fuerza <math>\vec F_{1,2}</math> ejercida por el sólido S1 sobre S2 , es opuesta a la fuerza <math> \ \vec F_{2,1}</math> ejercida por el sólido S2 sobre S1. Las dos fuerzas se encuentran sobre la misma línea de acción”.''''' | ||
| + | |||
| + | |||
| + | Este principio se aplica tanto a los sistemas en reposo como a los que se encuentran en movimiento. | ||
| + | |||
| + | Pero la ley de interacción crea a veces confusiones. Si un estudiante se apoya, de pie, contra un muro, la primera apreciación es que el estudiante se encuentra en equilibrio porque el muro ejerce sobre él una fuerza de reacción. Sin embargo, si va provisto de patines de ruedas y adopta la misma postura, se escurrirá hacia el suelo porque las ruedas de los patines se pondrán a rodar. Entonces ¿Quién lo sujeta? Se hace necesario pensar en el rozamiento de sus pies con el suelo que impide que se desplacen algo que de lo que no es capaz la fuerza de rozamiento de las ruedas de los patines con el suelo. | ||
| + | |||
| + | |||
| + | [[Imagen:Rozamiento_pared.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | El alumno no se caerá en tanto que las fuerzas de rozamiento <math>\vec Fr</math> de sus pies con el suelo sea mayor que la componente horizontal de la fuerza <math>\vec F_x</math> que ejercen sus pies contra el suelo. La componente <math>\vec F_y</math> se anula con la fuerza de reacción del suelo, <math>\vec R</math>. | ||
| + | |||
| + | Cuando se apoya sobre unos patines, la <math>\vec F_r</math> es mucho menos que <math>\vec F_x</math> y y las ruedas de los patines rodarán llevándolo hacia el suelo. Para que el alumno no se caiga es preciso mantener los pies en vertical de forma que <math>\vec F</math> sea lo más vertical posible y la componente <math>\vec F_y</math> - que se anule con la fuerza de reacción- sea mucho mayor <math>\vec F_x</math> , que es la que le obligaría a rodar los pies hacia delante, y ésta mucho menor que <math>\vec F_r</math> . | ||
| + | |||
| + | Cómo se ve la parte del cuerpo que juega un papel fundamental son los pies | ||
| + | |||
| + | |||
| + | [[Imagen:Rozamiento_pared_caida.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | Una duda similar se plantea cuando salta un saltador de longitud. Todo depende del golpe que da contra el suelo y como gestiona ese impulso en el aire con su juego de brazos y pies. Sin embargo el deportista se comporta igual que una pelota: cuanto más fuerte la lancemos contra el suelo más arriba votará. El deportista es devuelto hacia arriba por el suelo, al igual que la pelota, y juega con los pies y manos para conservar durante más tiempo la energía adquirida con el golpe. Hay una '''''acción''''', la del deportista y una '''''reacción''''', la del suelo. | ||
| + | |||
| + | |||
| + | === Fuerzas interiores en un sistema y fuerzas exteriores === | ||
| + | |||
| + | '''Sistema material''' | ||
| + | |||
| + | Un sólido o un conjunto de sólidos, sea este conjunto deformable o no, constituye un '''''sistema material S'''''. Todo aquello que no pertenezca al sistema se califica '''''de medio exterior E .''''' | ||
| + | |||
| + | Es necesario definir de manera bien precisa el sistema escogido antes de realizar un cualquier balance de fuerzas. | ||
| + | |||
| + | Una vez escogido el sistema, podremos clasificar las fuerzas ejercidas sobre cada punto o cada objeto del sistema limitado en dos tipos: | ||
| + | |||
| + | |||
| + | '''''Fuerzas exteriores,''''' son las que ejerce '''''E''''' sobre '''''S'''''. | ||
| + | '''''Fuerzas Interiores,''''' son las ejercidas por otro punto o por un objeto perteneciente a '''''S sobre una parte de S.''''' | ||
| + | |||
| + | |||
| + | '''''La suma de las fuerzas interiores es nula. Las fuerzas se anulan de dos en dos en base al principio de acción y reacción.''''' | ||
| + | |||
| + | Sin embargo, cuando aislamos una parte del sistema para realizar un balance de fuerzas, algunas de las fuerzas ''que son fuerzas interiores de'' '''''S,''''' ''resultan ser fuerzas exteriores a la parte del sistema considerada. '' | ||
| + | |||
| + | Sirva como ejemplo el considerado al suspender una masa de un resorte, o el del patinador. La resultante de las fuerzas aplicadas sobre <math>S_2</math> es una fuerza exterior de <math>S_1</math>. | ||
| + | |||
| + | === Relación entre masa y peso === | ||
| + | |||
| + | Hemos visto cómo podemos medir el peso de un sólido suspendiéndolo de un resorte. En el equilibrio, la fuerza elástica del resorte se hace igual al peso e impide que el sólido siga moviéndose. | ||
| + | |||
| + | Pero, ya se ha dicho, que todos los cuerpos que se encuentren alrededor de la Tierra sufren con ésta una interacción y es precisamente esa interacción la que hace que todo cuerpo abandonado a sí mismo se precipita sobre la Tierra. Pero esa '''''acción''''' ejercida por la Tierra depende de la masa de la Tierra y de la distancia a la que se el cuerpo se encuentre y podemos concluir pues, que en cada punto del entorno de la Tierra existe una magnitud que llamamos '''''intensidad de la gravedad''''' en el punto considerado. En el SI '''''g''''' se expresa siempre en <math>N . kg^1</math>, es decir podemos definirla como '''''la fuerza que sufre un cuerpo por unidad de masa. ''''' ''Esta propiedad del espacio que rodea la Tierra existe pues antes que coloquemos el cuerpo en ese punto puesto que es independiente de su masa.'' | ||
| + | |||
| + | Podemos escribir <math>\frac{P}{m} \ = g </math> de donde se puede deducir la expresión bien conocida P = m g, pero si expresamos la intensidad o módulo de los vectores P y g, escribiremos <math>P = - m g</math>. El signo negativo se debe a que el sentido tanto del peso como de la gravedad es hacia abajo, el opuesto al de las distancias referidas al centro de la Tierra. | ||
| + | |||
| + | Hemos dicho que la intensidad de la gravedad es diferente en cada punto de la superficie terrestre, varía desde <math>g = 9.78 N . kg^{-1}</math> en el polo norte hasta <math>g = 9,83 N.kg^{-1}</math>. El valor <math>g = 9,81 N . kg^{-1}</math> que se toma habitualmente es porque ese es el valor de g en París, que fue, en competencia con Cambridge, el centro de la ciencia hasta mediados del siglo XIX. | ||
| + | |||
| + | El peso de un cuerpo es diferente en la superficie de cada cuerpo astral. No es lo mismo en la Tierra que en la Luna, aunque no nos debe servir como referencia el célebre paseo que se da Amstrong – el astronauta -sobre la superficie lunar, con la bandera americana ondeando al viento – ¿Cuál, si en la Luna no hay atmósfera? – de aquel inmenso fraude que fue la película sobre el alunizaje del módulo lunar Tagle de la misión Apolo XI. Neil Amstrong y Edwin Aldrin pusieron los pies en la Luna el 20 de julio de 1969, y pudieron sentir que en la Luna pesaban menos, pero las imáginis distribuidas en el mundo habían estado filmadas con anterioridad por si la misión salía mal. No todo el limpio en la investigación científica. | ||
| + | |||
| + | El peso de un cuerpo no es igual pero la masa sí. Si suspendemos la masa de 1 kg de un dinamómetro sobre la Luna se alargará menos que lo hacía en la Tierra. Sin embargo dos masas de 1 kg dispuestas en sendos platos de una balanza se equilibran, pongamos esa balanza y esas masas en el lugar del universo que podamos imaginar. | ||
| + | |||
| + | [[Categoría:Física]] | ||
Revisión actual
Tabla de contenidos |
Interacciones mecánicas
Si revisamos algunos de los casos vistos al estudiar la naturaleza de las fuerzas, veremos como, en cada caso, existe una interacción entre el cuerpo y la acción aplicada sobre él.
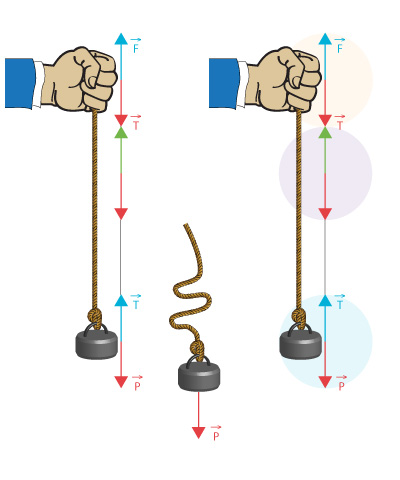
Si suspendemos una masa por el extremo de un hilo inextensible, y sujetamos con los dedos el otro extremo, aparecen sendas interacciones entre la masa y el hilo por un lado y entre el hilo y la mano por otro. A la fuerza que tira de la masa hacia abajo, su Peso, se opone el hilo con la tensión que sufre 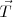 . Pero
. Pero 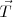 es consecuencia de que el hilo sea inextensible, y sin romperse. Se encuentra sobre cada punto del hilo – si lo cortamos, la masa cae pero el hilo pierde la forma vertical porque
es consecuencia de que el hilo sea inextensible, y sin romperse. Se encuentra sobre cada punto del hilo – si lo cortamos, la masa cae pero el hilo pierde la forma vertical porque 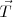 deja de existir-. También en el extremo que sujetamos con la mano, nosotros ejercemos una fuerza igual y de signo opuesto, es decir hacia arriba, a la tensión en ese punto.
deja de existir-. También en el extremo que sujetamos con la mano, nosotros ejercemos una fuerza igual y de signo opuesto, es decir hacia arriba, a la tensión en ese punto.
Si soltamos, la tensión desaparece. No hay pues tensiones negativas, la tensión existe o no existe, y por lo tanto, si existe, su signo es positivo. Sin embargo, si adoptamos como criterio de signos que la tensión con sentido hacia arriba es positiva, cuando vaya hacia abajo será negativa. En cualquier punto del hilo, salvo en los extremos, estarán presentes ambos vectores de modo que su suma sea cero, pero hablaremos de la Tensión, de una sola.
Si queremos estudiar las interacciones de un modelo separado aislamos la parte del sistema a estudiar, como se señala con las líneas roja y azul, respectivamente. En los extremos del hilo tendremos 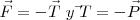 .
.
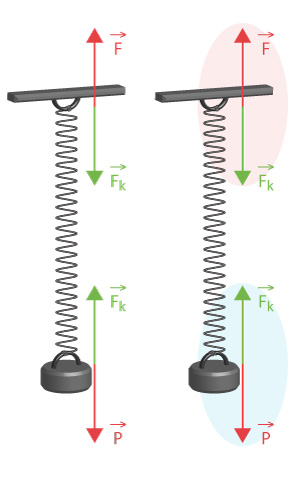
Cuando suspendemos una masa de un resorte, que se encuentre suspendido de una barra horizontal en el sistema existen interacciones entre la masa y el resorte y el resorte y la varilla.
La masa ejerce una acción sobre el resorte igual a su peso P , por su parte el resorte se opone a su alargamiento con su fuerza elástica, hasta que, al llegar al equilibrio,esa fuerza se hace igual al peso pero con sentido opuesto, es decir, hacia arriba. Por su parte el resorte, por el extremo superior, actúa sobre la varilla con una acción igual a su fuerza elástica. Si la varilla es indeformable, ésta actúa sobre el resorte con una fuerza igual y de sentido opuesto, pues de lo contrario la varilla cedería.
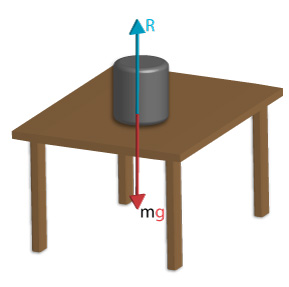
Del mismo modo cuando estudiamos el sistema formado por el cilindro y la mesa, colegimos que el cilindro es sostenido por el tablero pues de lo contrario caería al suelo.
El cilindro ejerce una acción sobre la mesa igual a su peso 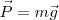 , que es vertical. El tablero debe ejercer una fuerza igual de sentido contrario, Fuerza de Reacción, R, perpendicular al plano de la mesa, que se encontrará distribuida entre todos los puntos de la base del cilindro.
, que es vertical. El tablero debe ejercer una fuerza igual de sentido contrario, Fuerza de Reacción, R, perpendicular al plano de la mesa, que se encontrará distribuida entre todos los puntos de la base del cilindro.
Hasta aquí hemos visto algunos ejemplos de las interacciones de las fuerzas de contacto, pero ¿Qué ocurre con las fuerzas a distancia? ¿Por qué un cuerpo cae hacia la Tierra y por qué la Luna evoluciona alrededor de la Tierra sin precipitarse sobre nosotros?¿Por qué la Tierra evoluciona alrededor del Sol y no continua su viaje espacial en línea recta?
La Tierra ejerce una fuerza sobre todos los cuerpos que depende de su masa respectiva, de la distancia a cada cuerpo y de la masa de la Tierra. Esa fuerza es muy grande con relación a la masa de cada cuerpo y la acción que ejerce la Tierra les obliga a precipitarse sobre el suelo. Sin embargo esa fuerza es muy pequeña para desplazar a la Tierra de su posición o desviar su trayectoria.
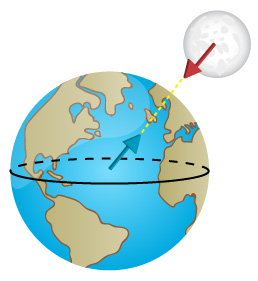
La Tierra atrae a la Luna con una acción tal que sólo, y nada menos, puede hacer variar la dirección de su movimiento, obligándola a evolucionar alrededor de la Tierra. La Luna ejerce una fuerza igual y de signo contrario sobre la Tierra, pero la masa de la tierra es muy grande para desviar su trayectoria, sin embargo, como se verá, sí que influye sobre la altura de las mareas.
La acción que ejerce la Tierra sobre la Luna, 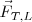 , es igual y de sentido opuesto a la reacción de la Luna sobre la tierra,
, es igual y de sentido opuesto a la reacción de la Luna sobre la tierra, 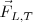 Ambas fuerzas se encuentran aplicadas sobre el centro de la Luna y de la Tierra, respectivamente, y su dirección es la de la línea que los une.
Ambas fuerzas se encuentran aplicadas sobre el centro de la Luna y de la Tierra, respectivamente, y su dirección es la de la línea que los une.
Del mismo modo podemos plantear la existencia de dos fuerzas iguales y de sentido opuesto cuando se trata de fuerzas eléctricas que son también fuerzas a distancia.
Principio de Acciones Recíprocas o Principio de Acción y Reacción
Es de todo punto evidente que para existir, una fuerza debe ser ejercida por algo o alguien sobre otro cuerpo. Del mismo modo, un cuerpo no puede ser empujado (o arrastrado) si no hay al menos algo que lo empuje o lo arrastre. Es decir, podemos afirmar que en la naturaleza las fuerzas existen a pares de tal modo que una se opone a la otra. No hay fuerzas aisladas, sólo existen interacciones entre los cuerpos, y el problema radica en saber quien empuja y quien es empujado, o quien tira y quien es arrastrado.
Siempre que en el sistema estudiado aparece un organismo vivo, hay una tendencia a creer que es él el que ejerce la acción. En la mina, siempre imaginamos al minero empujando la vagoneta y no al revés. Sin embargo, esta creencia desaparece cuando se trata de dos objetos inanimados.
Si en el mercado nos pesan un kilogramo de carne sobre una balanza de torsión, llegamos sin dificultad a la conclusión de que la carne ejerce una acción sobre el plato de la balanza, y que éste ejerce sobre la carne una fuerza igual y de signo opuesto. Newton, enunció lo que hoy llamamos 3ª Ley de Newton o Principio de acción y reacción, “A toda acción le corresponde una reacción de igual intensidad y sentido contrario”.
Este enunciado parece que privilegia una de las fuerzas, la acción, sobre la otra, la de reacción, cuando ambas fuerzas ejercen el mismo papel en el estado del sistema material estudiado, y que no puede existir la una sin la otra. Por eso hoy este principio queda mejor expresado de otra forma:
“Si dos sólidos S1 y S2 se encuentran en interacción mecánica, la fuerza 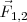 ejercida por el sólido S1 sobre S2 , es opuesta a la fuerza
ejercida por el sólido S1 sobre S2 , es opuesta a la fuerza 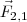 ejercida por el sólido S2 sobre S1. Las dos fuerzas se encuentran sobre la misma línea de acción”.
ejercida por el sólido S2 sobre S1. Las dos fuerzas se encuentran sobre la misma línea de acción”.
Este principio se aplica tanto a los sistemas en reposo como a los que se encuentran en movimiento.
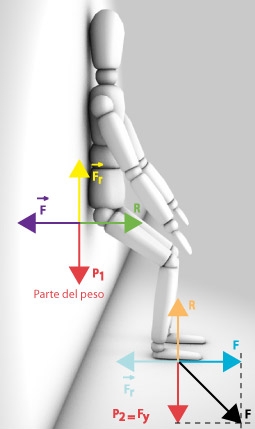
Pero la ley de interacción crea a veces confusiones. Si un estudiante se apoya, de pie, contra un muro, la primera apreciación es que el estudiante se encuentra en equilibrio porque el muro ejerce sobre él una fuerza de reacción. Sin embargo, si va provisto de patines de ruedas y adopta la misma postura, se escurrirá hacia el suelo porque las ruedas de los patines se pondrán a rodar. Entonces ¿Quién lo sujeta? Se hace necesario pensar en el rozamiento de sus pies con el suelo que impide que se desplacen algo que de lo que no es capaz la fuerza de rozamiento de las ruedas de los patines con el suelo.
El alumno no se caerá en tanto que las fuerzas de rozamiento 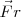 de sus pies con el suelo sea mayor que la componente horizontal de la fuerza
de sus pies con el suelo sea mayor que la componente horizontal de la fuerza 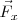 que ejercen sus pies contra el suelo. La componente
que ejercen sus pies contra el suelo. La componente 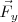 se anula con la fuerza de reacción del suelo,
se anula con la fuerza de reacción del suelo, 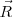 .
.
Cuando se apoya sobre unos patines, la 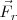 es mucho menos que
es mucho menos que 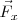 y y las ruedas de los patines rodarán llevándolo hacia el suelo. Para que el alumno no se caiga es preciso mantener los pies en vertical de forma que
y y las ruedas de los patines rodarán llevándolo hacia el suelo. Para que el alumno no se caiga es preciso mantener los pies en vertical de forma que 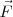 sea lo más vertical posible y la componente
sea lo más vertical posible y la componente 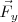 - que se anule con la fuerza de reacción- sea mucho mayor
- que se anule con la fuerza de reacción- sea mucho mayor 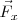 , que es la que le obligaría a rodar los pies hacia delante, y ésta mucho menor que
, que es la que le obligaría a rodar los pies hacia delante, y ésta mucho menor que 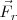 .
.
Cómo se ve la parte del cuerpo que juega un papel fundamental son los pies
Una duda similar se plantea cuando salta un saltador de longitud. Todo depende del golpe que da contra el suelo y como gestiona ese impulso en el aire con su juego de brazos y pies. Sin embargo el deportista se comporta igual que una pelota: cuanto más fuerte la lancemos contra el suelo más arriba votará. El deportista es devuelto hacia arriba por el suelo, al igual que la pelota, y juega con los pies y manos para conservar durante más tiempo la energía adquirida con el golpe. Hay una acción, la del deportista y una reacción, la del suelo.
Fuerzas interiores en un sistema y fuerzas exteriores
Sistema material
Un sólido o un conjunto de sólidos, sea este conjunto deformable o no, constituye un sistema material S. Todo aquello que no pertenezca al sistema se califica de medio exterior E .
Es necesario definir de manera bien precisa el sistema escogido antes de realizar un cualquier balance de fuerzas.
Una vez escogido el sistema, podremos clasificar las fuerzas ejercidas sobre cada punto o cada objeto del sistema limitado en dos tipos:
Fuerzas exteriores, son las que ejerce E sobre S.
Fuerzas Interiores, son las ejercidas por otro punto o por un objeto perteneciente a S sobre una parte de S.
La suma de las fuerzas interiores es nula. Las fuerzas se anulan de dos en dos en base al principio de acción y reacción.
Sin embargo, cuando aislamos una parte del sistema para realizar un balance de fuerzas, algunas de las fuerzas que son fuerzas interiores de S, resultan ser fuerzas exteriores a la parte del sistema considerada.
Sirva como ejemplo el considerado al suspender una masa de un resorte, o el del patinador. La resultante de las fuerzas aplicadas sobre 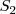 es una fuerza exterior de
es una fuerza exterior de 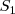 .
.
Relación entre masa y peso
Hemos visto cómo podemos medir el peso de un sólido suspendiéndolo de un resorte. En el equilibrio, la fuerza elástica del resorte se hace igual al peso e impide que el sólido siga moviéndose.
Pero, ya se ha dicho, que todos los cuerpos que se encuentren alrededor de la Tierra sufren con ésta una interacción y es precisamente esa interacción la que hace que todo cuerpo abandonado a sí mismo se precipita sobre la Tierra. Pero esa acción ejercida por la Tierra depende de la masa de la Tierra y de la distancia a la que se el cuerpo se encuentre y podemos concluir pues, que en cada punto del entorno de la Tierra existe una magnitud que llamamos intensidad de la gravedad en el punto considerado. En el SI g se expresa siempre en 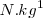 , es decir podemos definirla como la fuerza que sufre un cuerpo por unidad de masa. Esta propiedad del espacio que rodea la Tierra existe pues antes que coloquemos el cuerpo en ese punto puesto que es independiente de su masa.
, es decir podemos definirla como la fuerza que sufre un cuerpo por unidad de masa. Esta propiedad del espacio que rodea la Tierra existe pues antes que coloquemos el cuerpo en ese punto puesto que es independiente de su masa.
Podemos escribir 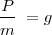 de donde se puede deducir la expresión bien conocida P = m g, pero si expresamos la intensidad o módulo de los vectores P y g, escribiremos
de donde se puede deducir la expresión bien conocida P = m g, pero si expresamos la intensidad o módulo de los vectores P y g, escribiremos 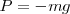 . El signo negativo se debe a que el sentido tanto del peso como de la gravedad es hacia abajo, el opuesto al de las distancias referidas al centro de la Tierra.
. El signo negativo se debe a que el sentido tanto del peso como de la gravedad es hacia abajo, el opuesto al de las distancias referidas al centro de la Tierra.
Hemos dicho que la intensidad de la gravedad es diferente en cada punto de la superficie terrestre, varía desde 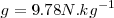 en el polo norte hasta
en el polo norte hasta 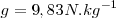 . El valor
. El valor 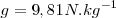 que se toma habitualmente es porque ese es el valor de g en París, que fue, en competencia con Cambridge, el centro de la ciencia hasta mediados del siglo XIX.
que se toma habitualmente es porque ese es el valor de g en París, que fue, en competencia con Cambridge, el centro de la ciencia hasta mediados del siglo XIX.
El peso de un cuerpo es diferente en la superficie de cada cuerpo astral. No es lo mismo en la Tierra que en la Luna, aunque no nos debe servir como referencia el célebre paseo que se da Amstrong – el astronauta -sobre la superficie lunar, con la bandera americana ondeando al viento – ¿Cuál, si en la Luna no hay atmósfera? – de aquel inmenso fraude que fue la película sobre el alunizaje del módulo lunar Tagle de la misión Apolo XI. Neil Amstrong y Edwin Aldrin pusieron los pies en la Luna el 20 de julio de 1969, y pudieron sentir que en la Luna pesaban menos, pero las imáginis distribuidas en el mundo habían estado filmadas con anterioridad por si la misión salía mal. No todo el limpio en la investigación científica.
El peso de un cuerpo no es igual pero la masa sí. Si suspendemos la masa de 1 kg de un dinamómetro sobre la Luna se alargará menos que lo hacía en la Tierra. Sin embargo dos masas de 1 kg dispuestas en sendos platos de una balanza se equilibran, pongamos esa balanza y esas masas en el lugar del universo que podamos imaginar.
Tweet