Ecuaciones de la recta en el espacio
De Wikillerato
(→Ecuacion en forma vectorial) |
(→Ecuación en forma continua) |
||
| (28 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
<br/> | <br/> | ||
| - | Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un | + | Al igual que ocurre en el plano, una '''recta''' en el espacio queda determinada conociendo un |
punto | punto | ||
<math> | <math> | ||
| Línea 19: | Línea 19: | ||
<br/> | <br/> | ||
| - | == | + | ==Ecuacion en forma vectorial== |
| - | + | ||
<br/> | <br/> | ||
| Línea 99: | Línea 98: | ||
<br/> | <br/> | ||
| - | Desarrollando la ecuación vectorial anterior expresada en coordenadas, tenemos: | + | Desarrollando la ecuación vectorial anterior expresada en coordenadas, tenemos lo siguiente: |
<br/> | <br/> | ||
| Línea 155: | Línea 154: | ||
<br/> | <br/> | ||
| - | Si, en las ecuaciones paramétricas, | + | Si, en las ecuaciones '''paramétricas''', |
<math> | <math> | ||
v_x | v_x | ||
| Línea 201: | Línea 200: | ||
<br/> | <br/> | ||
| - | ==Ecuación en forma cartesiana o implícita== | + | ==Ecuación en forma cartesiana o implícita (Recta como intersección de dos planos)== |
<br/> | <br/> | ||
| - | A partir de la ecuación | + | A partir de la ecuación forma continua de la recta podemos obtener las dos ecuaciones |
siguientes: | siguientes: | ||
| Línea 246: | Línea 245: | ||
y que se conocen con el nombre '''''de ecuación implícita''''' o '''''cartesiana''''' de | y que se conocen con el nombre '''''de ecuación implícita''''' o '''''cartesiana''''' de | ||
| - | la recta. | + | la recta. (Recta como intersección de dos planos) |
<br/> | <br/> | ||
Revisión actual
Tabla de contenidos |
Introducción
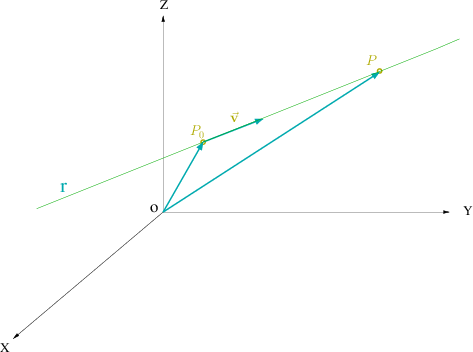
Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un
punto
 y un vector no nulo
y un vector no nulo
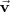 que se llama vector director o direccional de la recta.
que se llama vector director o direccional de la recta.
Estudiamos a continuacion las diferentes formas que puede adoptar la ecuacion de una recta.
Ecuacion en forma vectorial
La recta que pasa por el punto
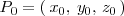 y tiene por vector director
y tiene por vector director
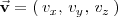 es el conjunto de puntos
es el conjunto de puntos
 del espacio que verifican la relacion vectorial
del espacio que verifican la relacion vectorial
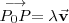 con
con
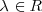
Teniendo en cuenta la suma de vectores se verifica que:
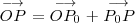
Si identificamos el punto
 con el vector que va desde el origen de coordenadas hasta el punto
con el vector que va desde el origen de coordenadas hasta el punto
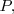
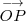 , se tiene que
, se tiene que
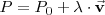
que se denomina ecuación vectorial de la recta.
Ecuación en forma paramétrica
Desarrollando la ecuación vectorial anterior expresada en coordenadas, tenemos lo siguiente:
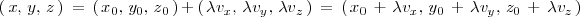
Igualando componentes resulta:
![r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & x_0 \, + \, \lambda v_x
\\
y & = & y_0 \, + \, \lambda v_y
\\
z & = & z_0 \, + \, \lambda v_z
\end{array}
</pre>
<p>\right.
r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & x_0 \, + \, \lambda v_x
\\
y & = & y_0 \, + \, \lambda v_y
\\
z & = & z_0 \, + \, \lambda v_z
\end{array}
</pre>
<p>\right.](/images/math/math-438d99d857893623546d84c8c3c24795.png)
Expresión que se denomina ecuación de la recta en forma paramétrica o ecuaciones paramétricas de la recta.
Ecuación en forma continua
Si, en las ecuaciones paramétricas,
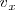 ,
,
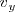 y
y
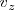 son distintos de cero, se puede despejar en cada una de ellas el parametro
son distintos de cero, se puede despejar en cada una de ellas el parametro
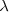
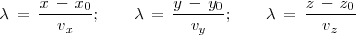
Igualando las expresiones obtenidas resulta:
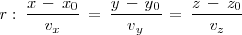
que es la ecuación de la recta en forma continua.
Ecuación en forma cartesiana o implícita (Recta como intersección de dos planos)
A partir de la ecuación forma continua de la recta podemos obtener las dos ecuaciones siguientes:
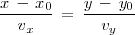
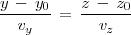
que se pueden reescribir de la forma:
![r: \,
\left\{
</p>
<pre> \begin{array}[c]{c}
a \cdot x \, + \, b \cdot y \, + \, c \cdot z \, + \, d \, = \, 0
\\
a^\prime \cdot x \, + \, b^\prime \cdot y \, + \, c^\prime \cdot z \, + \, d^\prime \, = \, 0
\end{array}
</pre>
<p>\right.
r: \,
\left\{
</p>
<pre> \begin{array}[c]{c}
a \cdot x \, + \, b \cdot y \, + \, c \cdot z \, + \, d \, = \, 0
\\
a^\prime \cdot x \, + \, b^\prime \cdot y \, + \, c^\prime \cdot z \, + \, d^\prime \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-d32e0aa2f0d79ba74e8ea9a7f4a7a04f.png)
y que se conocen con el nombre de ecuación implícita o cartesiana de la recta. (Recta como intersección de dos planos)
Ejemplo
Determinemos las ecuaciones de la recta
 que pasa por los puntos:
que pasa por los puntos:

Un vector director de
 es, por ejemplo, el vector que va desde el punto
es, por ejemplo, el vector que va desde el punto
 hasta el punto
hasta el punto
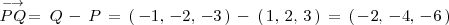
Por lo tanto, la ecuacion de la recta
 en forma vectorial es:
en forma vectorial es:
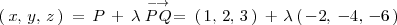
En forma paramétrica es:
![r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, - \, 2 \lambda
\\
y & = & 2 \, - \, 4 \lambda
\\
z & = & 3 \, - \, 6 \lambda
\end{array}
</pre>
<p>\right.
r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, - \, 2 \lambda
\\
y & = & 2 \, - \, 4 \lambda
\\
z & = & 3 \, - \, 6 \lambda
\end{array}
</pre>
<p>\right.](/images/math/math-b351b760a11cb2abb33afe248de235dc.png)
En forma continua es:
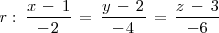
En forma implicita es:
![r: \,
\left\{
</p>
<pre> \begin{array}[c]{c}
2 \cdot x \, - \, y \, = \, 0
\\
3 \cdot x \, - \, z \, = \, 0
\end{array}
</pre>
<p>\right.
r: \,
\left\{
</p>
<pre> \begin{array}[c]{c}
2 \cdot x \, - \, y \, = \, 0
\\
3 \cdot x \, - \, z \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-6bdbf8b6d9ccc4a972a6b5f84f6ffeba.png)