Ley fundamental de la Dinámica
De Wikillerato
(→Sistema referencial galileano) |
(→Fuerza y cantidad de movimiento) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
Se llama fuerza a una acción mecánica que conlleva una variación de la cantidad de movimiento del sistema. | Se llama fuerza a una acción mecánica que conlleva una variación de la cantidad de movimiento del sistema. | ||
| - | + | y a los tontos que leen esto | |
== Relación fundamental de la dinámica == | == Relación fundamental de la dinámica == | ||
| - | Si en un instante t muy próximo a <math>t + \Delta t</math> , un móvil es sometido a la acción de una fuerza <math>f | + | Si en un instante t muy próximo a <math>t + \Delta t</math> , un móvil es sometido a la acción de una fuerza <math>\vec f</math>, la variación de la cantidad de movimiento <math>d\vec p</math> tiene la misma dirección y sentido que <math>\vec f</math>. Dado que <math>dt</math> es un escalar y siempre positivo, el vector <math>\frac{d \vec p}{dt}</math> tiene, además de la misma dirección y sentido, el mismo módulo que <math> \vec f</math>. '''''Podemos pues decir que la fuerza aplicada <math>\vec f</math> es igual a la variación temporal del vector cantidad de movimiento.''''' |
<math> \vec f = \frac {d \vec p} {dt}</math> | <math> \vec f = \frac {d \vec p} {dt}</math> | ||
| - | Si | + | Si un sólido es sometido a la acción de diversas fuerzas cuya suma vectorial es <math>\sum \vec f</math> podremos escribir igualmente |
<math> \sum \vec f \ = \frac {d \vec p} {dt}</math> | <math> \sum \vec f \ = \frac {d \vec p} {dt}</math> | ||
| - | Esta afirmación que no demostramos en este momento es, sin embargo, verificada en numerosos fenómenos. Newton la utilizó para interpretar con éxito las leyes de Kepler referidas al movimiento de los planetas del sistema solar. Esta ley tiene pues el carácter de un ''postulado conocido como la ley fundamental de la dinámica'', bien entendido de la | + | Esta afirmación que no demostramos en este momento es, sin embargo, verificada en numerosos fenómenos. Newton la utilizó para interpretar con éxito las leyes de Kepler referidas al movimiento de los planetas del sistema solar. Esta ley tiene pues el carácter de un ''postulado conocido como la ley fundamental de la dinámica'', bien entendido de la mecánica newtoniana. |
| - | '''''En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un | + | '''''En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un sólido es igual a la derivada con respecto al tiempo del vector cantidad de movimiento del ese sólido.''''' |
== Aceleración del centro de inercia. Teorema del Centro de Inercia == | == Aceleración del centro de inercia. Teorema del Centro de Inercia == | ||
| Línea 172: | Línea 172: | ||
Así, por ejemplo, si un sistema referencial terrestre es galileano, también lo es un sistema referencial ligado a un vehículo que se mueve con movimiento rectilíneo y uniforme con relación a la Tierra. Por ejemplo, los peatones que avanzan en un una pasillo móvil, los vajeros que se mueven en el ave se encuentran en sistemas referenciales galileanos. Esto significa que la relación <math>\sum \vec f = \frac {d \vec p} {dt}</math> puede ser aplicada tanto al sistema referencial terrestre como al sistema referencial ligado al pasillo o al ''ave''. Utilizando esta relación no es posible desvelar el moviento rectilíneo y uniforme del vehículo. De este modo, si el tren pasa por un tunel y están apagadas las luces, dado que el vagón del ''ave'' se encuentra insonorizado, el viajero no podría precisar si el vagón se encuentra en movimiento o está parado. | Así, por ejemplo, si un sistema referencial terrestre es galileano, también lo es un sistema referencial ligado a un vehículo que se mueve con movimiento rectilíneo y uniforme con relación a la Tierra. Por ejemplo, los peatones que avanzan en un una pasillo móvil, los vajeros que se mueven en el ave se encuentran en sistemas referenciales galileanos. Esto significa que la relación <math>\sum \vec f = \frac {d \vec p} {dt}</math> puede ser aplicada tanto al sistema referencial terrestre como al sistema referencial ligado al pasillo o al ''ave''. Utilizando esta relación no es posible desvelar el moviento rectilíneo y uniforme del vehículo. De este modo, si el tren pasa por un tunel y están apagadas las luces, dado que el vagón del ''ave'' se encuentra insonorizado, el viajero no podría precisar si el vagón se encuentra en movimiento o está parado. | ||
| - | De todo se concluye que la relación <math>\sum \vec f = \frac {d \vec p} {dt} </math> es una invariante en todos los sistemas referenciales galileanos. | + | De todo se concluye que la relación <math>\sum \vec f = \frac {d \vec p} {dt} </math> '''''es una invariante en todos los sistemas referenciales galileanos.''''' |
| + | |||
| + | [[Categoría:Física]] | ||
Revisión actual
Tabla de contenidos |
Fuerza y cantidad de movimiento
Cuando un sistema, cuya masa supondremos concentrada en su centro de inercia, es sometido a la acción de fuerzas exteriores que no se compensan entre sí , su vector velocidad varía. Si el cuerpo se encontraba en reposo se pondrá en movimiento, y si se encontraba en movimiento se modifica su vector velocidad.
Se llama fuerza a una acción mecánica que conlleva una variación de la cantidad de movimiento del sistema. y a los tontos que leen esto
Relación fundamental de la dinámica
Si en un instante t muy próximo a 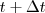 , un móvil es sometido a la acción de una fuerza
, un móvil es sometido a la acción de una fuerza 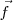 , la variación de la cantidad de movimiento
, la variación de la cantidad de movimiento 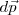 tiene la misma dirección y sentido que
tiene la misma dirección y sentido que 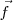 . Dado que
. Dado que 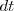 es un escalar y siempre positivo, el vector
es un escalar y siempre positivo, el vector 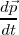 tiene, además de la misma dirección y sentido, el mismo módulo que
tiene, además de la misma dirección y sentido, el mismo módulo que 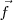 . Podemos pues decir que la fuerza aplicada
. Podemos pues decir que la fuerza aplicada 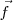 es igual a la variación temporal del vector cantidad de movimiento.
es igual a la variación temporal del vector cantidad de movimiento.
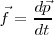
Si un sólido es sometido a la acción de diversas fuerzas cuya suma vectorial es 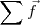 podremos escribir igualmente
podremos escribir igualmente
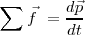
Esta afirmación que no demostramos en este momento es, sin embargo, verificada en numerosos fenómenos. Newton la utilizó para interpretar con éxito las leyes de Kepler referidas al movimiento de los planetas del sistema solar. Esta ley tiene pues el carácter de un postulado conocido como la ley fundamental de la dinámica, bien entendido de la mecánica newtoniana.
En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un sólido es igual a la derivada con respecto al tiempo del vector cantidad de movimiento del ese sólido.
Aceleración del centro de inercia. Teorema del Centro de Inercia
Si sustituímos  por su valor
por su valor 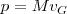 y calculamos su derivada, dado que la masa
y calculamos su derivada, dado que la masa 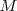 es una constante y la aceleración es la derivada de la velocidad con relación al tiempo, tenemos:
es una constante y la aceleración es la derivada de la velocidad con relación al tiempo, tenemos:
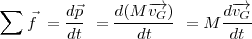
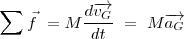
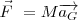
Teorema del centro de inercia: En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un sólido es igual al producto de su masa por el vector aceleración de su centro de inercia.
Atención
Al hallar la suma vectorial de las fuerzas aplicadas sobre el sólido no debemos olvidar nunca el pso P del mismo.
Para obtener el vector aceleración del centro de inercia del sólido, consideramos que toda la masa del sólido se encuentra concentrada en ese punto y aplicamos sobre el mismo el conjunto de fuerzas que se ejercen sobre el sólido. Hablamos de un cuerpo puntual
Unidades
La conocida fórmula 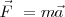 o más propiamente escrita
o más propiamente escrita
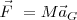 en el SI debemos expresar las magnitudes en las siguientes unidades
en el SI debemos expresar las magnitudes en las siguientes unidades  en Newtons,
en Newtons, 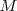 o
o 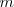 en
en 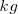 y
y  en
en 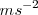 o en
o en 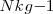 .
.
D este modo podemos definir el Newton como la intensidad de una fuerza que aplicada de un modo continuo sobre un sólido cuya masa es de 1 kg,le comunica una aceleración de 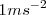
Relación causa-efecto
Efectivamente, son las fuerzas aplicadas las que provocan el movimiento del centro de masas o centro de inercia de un sólido, es decir son la causa y su efecto se presenta bajo la forma de una aceleración del centro de inercia G. Pero esta aceleración se encuentra <<modulada>> por la masa del sólido, es decir, por un efecto de la inercia.
Para una fuerza F feterminada, la aceleración a que adquiere el centro de inercia es tanto más pequeña cuanto mayor sea la masa M. Diremos que la aceleración adquirida por el sólido es tanto menor cuanto mayor sea la inercia del sólido, es decir, su masa.
Podemos pues presentarlo de la forma siguiente
Caso particular. Sólido sometido a la acción de una fuerza constante
Sabemos que 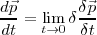 Sin embargo si
Sin embargo si 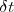 no es infinitamente pequeño sino solamente pequeño podemos esctibir con poco error
no es infinitamente pequeño sino solamente pequeño podemos esctibir con poco error
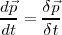 siendo
siendo
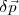 la variación de la cantidad de movimiento en el tiempo
la variación de la cantidad de movimiento en el tiempo 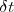 . Por lo tanto:
. Por lo tanto:
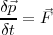
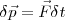
Si hacemos la hipótesis de que  mantiene el módulo, dirección y sentido entre dos instantes
mantiene el módulo, dirección y sentido entre dos instantes 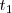 y
y 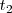 en los cuales las velocidades del centro de inercia del sólido son
en los cuales las velocidades del centro de inercia del sólido son 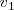 y
y 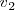 La relación vectorial puede escribirse como si los vectores fueran escalares.
La relación vectorial puede escribirse como si los vectores fueran escalares.
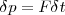
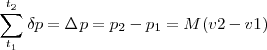
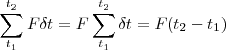
de donde se obtiene :
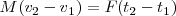
A la magnitud 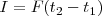 se le llema impulso lineal que es igual a la variación de la cantidad de movimiento.
se le llema impulso lineal que es igual a la variación de la cantidad de movimiento.
Elección de un sistema de referencia
Se ha introducido una restricción en el enunciado de la ley. La aplicaremos solamente en los sistemas referenciales galileanos. ¿Pero qué entendemos por tales sistemas referenciales ?
En un sistema referencial galileano un sólido en reposo, que no se encuentra sometido a fuerza exterior alguna, permanece en reposo. Si ese sólido no se encontraba en reposo el movimiento de su centro de inercia será rectilíneo y uniforme en ese sistema referencial. Estas afirmaciones constituyen el principio de inercia el cual aparece como un caso particular de la ley fundamental de la dinámica:
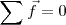
conduce a
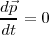 con lo cual
con lo cual 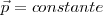
Si 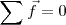 , el sólido tendrá una cantidad de movimiento constante y su centro de inercia se encuentra en reposo o con un movimiento rectilíneo y uniforme.
, el sólido tendrá una cantidad de movimiento constante y su centro de inercia se encuentra en reposo o con un movimiento rectilíneo y uniforme.
Pero nos encontramos con una dificultad experimental, si bien podemos evitar que el sólido sufra la acción de una fuerza de contacto (por ejemplo, rozamiento), es menos sencillo poder evitar que sea sometido a una acción a distancia al menos que hagamos la hipótesis de que se encuentra muy alejado de cualquier otro sólido. Esto nos obliga a escoger un sistema de referencia ligado a las estrellas, prácticamente fijas unas con relación a las otras a causa de las enormes distancias que las separan. En un tal sistema, un sólido muy alejado de cualquier otro no se encuentra sometido a acción exterior alguna y obedecerá entonces al principio de inercia.
Un sistema referencial ligado a las estrellas es un sistema referencial galileano.
Sistema referencial galileano
En astrofísica se utiliza en efecto sistemas galileanos muy prácticos : El sisteme referencial de Copérnico, con los ejes dirigidos hacia tres estrellas y cuyo origen se encuentra en el centro de inercia del sistema solar ; el sistema referencial de Kepler, con los ejes dirigidos hacia tres estrellas y cuyo origen es el centro de inercia del Sol, pero en nuestros estudios de mecánica, utilizaremos fundamentalmente dos:
Sistema referencial geocéntrico
Su origen se encuentra en le centro de la tierra y sus tres vectores unitarios se encuentran dirigidos hacia tres estrellas.
Aunque el sistema no sea rigurosamente galileano a causa del movimiento de la Tierra en el sistema solar, podemos considerarlo como tal con una gran precisión.
Sistema referencial terrestre
Un sistema referencial terrestre se encuentra ligado a la Tierra, al laboratorio por ejemplo. En un sistema geocéntrico éste gira gira alrededor del eje de los polos de la Tierra. El periodo de una revolución es un dia sideral, es decir, 86164 s y no es pues rigurosamente galileano. Sin embargo, salvo algunas excepciones, constituye un buen sistema referencial galileano pata la interpretación de experiencias y fenómenos que tienen lugar en la proximidad de la Tierra.
Propiedades de los sistemas referenciales galileanos
Admitiremos que un sistema referencial es galileano si podemos aplicar en esas referenciales la relación 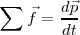 sin riesgo a que la experiencia lo desmienta.
sin riesgo a que la experiencia lo desmienta.
Se puede demostrar que si un sistema referencial es galileano , todos aquellos que con relación a él se encuentran en reposo o se mueven con movimiento rectilíneo y uniforme también lo son.
Así, por ejemplo, si un sistema referencial terrestre es galileano, también lo es un sistema referencial ligado a un vehículo que se mueve con movimiento rectilíneo y uniforme con relación a la Tierra. Por ejemplo, los peatones que avanzan en un una pasillo móvil, los vajeros que se mueven en el ave se encuentran en sistemas referenciales galileanos. Esto significa que la relación 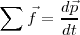 puede ser aplicada tanto al sistema referencial terrestre como al sistema referencial ligado al pasillo o al ave. Utilizando esta relación no es posible desvelar el moviento rectilíneo y uniforme del vehículo. De este modo, si el tren pasa por un tunel y están apagadas las luces, dado que el vagón del ave se encuentra insonorizado, el viajero no podría precisar si el vagón se encuentra en movimiento o está parado.
puede ser aplicada tanto al sistema referencial terrestre como al sistema referencial ligado al pasillo o al ave. Utilizando esta relación no es posible desvelar el moviento rectilíneo y uniforme del vehículo. De este modo, si el tren pasa por un tunel y están apagadas las luces, dado que el vagón del ave se encuentra insonorizado, el viajero no podría precisar si el vagón se encuentra en movimiento o está parado.
De todo se concluye que la relación 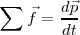 es una invariante en todos los sistemas referenciales galileanos.
es una invariante en todos los sistemas referenciales galileanos.



