Navegación
Transformaciones geométricas basadas en la proporcionalidad directa
De Wikillerato
(Deshacer vandalismo) |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | {{en desarrollo}} | ||
| + | |||
===Homología=== | ===Homología=== | ||
| Línea 5: | Línea 7: | ||
dos puntos homólogos <math>A</math> y <math>A'</math> están alineados con un punto fijo <math>O \ </math> que es el centro de la homología; dos rectas homólogas <math>r</math> y <math>r'</math> se cortan en una recta doble llamada eje de la homología; existe un coeficiente de homología, <math>\lambda = (OM A A')</math>, la razón doble en la que <math>O \ </math> es el centro, <math>A</math> y <math>A'</math> un par de homólogos y <math>M</math> el punto doble de la recta <math>OA</math>. | dos puntos homólogos <math>A</math> y <math>A'</math> están alineados con un punto fijo <math>O \ </math> que es el centro de la homología; dos rectas homólogas <math>r</math> y <math>r'</math> se cortan en una recta doble llamada eje de la homología; existe un coeficiente de homología, <math>\lambda = (OM A A')</math>, la razón doble en la que <math>O \ </math> es el centro, <math>A</math> y <math>A'</math> un par de homólogos y <math>M</math> el punto doble de la recta <math>OA</math>. | ||
| + | |||
| + | [[Imagen:22Homologia.gif]] | ||
===Homotecia=== | ===Homotecia=== | ||
| Línea 13: | Línea 17: | ||
<math>k</math> se llama razón de la homotecia. | <math>k</math> se llama razón de la homotecia. | ||
| + | |||
| + | [[Imagen:23Homotecia.gif]] | ||
===Afinidad=== | ===Afinidad=== | ||
| Línea 19: | Línea 25: | ||
Transforma los puntos del plano: <math>A, B, C....</math> en puntos del plano <math>A' ,B' ,C' ...</math>, de modo que: dos puntos homólogos <math>A</math> y <math>A'</math> definen un segmento paralelo a la dirección de afinidad <math>d \ </math>; dos rectas homólogas <math>r</math> y <math>r'</math> se cortan en una recta doble llamada <math>e</math>, eje de la afinidad; existe un coeficiente de afinidad, <math>\mu = MA'/MA</math>, la razón en la que <math>A</math> y <math>A'</math> son un par de homólogos y <math>M</math> el punto doble de la recta <math>AA'</math>. | Transforma los puntos del plano: <math>A, B, C....</math> en puntos del plano <math>A' ,B' ,C' ...</math>, de modo que: dos puntos homólogos <math>A</math> y <math>A'</math> definen un segmento paralelo a la dirección de afinidad <math>d \ </math>; dos rectas homólogas <math>r</math> y <math>r'</math> se cortan en una recta doble llamada <math>e</math>, eje de la afinidad; existe un coeficiente de afinidad, <math>\mu = MA'/MA</math>, la razón en la que <math>A</math> y <math>A'</math> son un par de homólogos y <math>M</math> el punto doble de la recta <math>AA'</math>. | ||
| + | |||
| + | [[Imagen:24Afinidad.gif]] | ||
===Simetrías=== | ===Simetrías=== | ||
Las simetrías son isomórficas e isométricas, pues mantienen la forma y el tamaño de las figuras. En el plano existen dos tipos de simetrías: la central y la axial. | Las simetrías son isomórficas e isométricas, pues mantienen la forma y el tamaño de las figuras. En el plano existen dos tipos de simetrías: la central y la axial. | ||
| - | La simetría central de un punto A respecto del centro O es el punto | + | La simetría central de un punto <math>A</math> respecto del centro <math>O \ </math> es el punto <math>A'</math>, alineado con <math>A</math> y <math>O \ </math>, de modo que <math>AO = OA'</math>. La simetría central es una homotecia con <math>k= -1</math>. |
| + | [[Imagen:25Simetrias.gif]] | ||
| - | La simetría axial de un punto A respecto del eje e es el punto | + | La simetría axial de un punto <math>A</math> respecto del eje e es el punto <math>A'</math>, siendo la recta <math>AA'</math> perpendicular al eje <math>e</math> y <math>A</math> y <math>A'</math> equidistantes del mismo. |
| - | La simetría axial es una afinidad con | + | |
| + | La simetría axial es una afinidad con <math>\mu = -1</math> | ||
| + | |||
| + | [[Imagen:26Simetrias.gif]] | ||
===Translaciones=== | ===Translaciones=== | ||
Las translaciones son isomórficas e isométricas. Son homologías con el eje y el centro en el infinito. | Las translaciones son isomórficas e isométricas. Son homologías con el eje y el centro en el infinito. | ||
| - | La translación de un punto A una magnitud m, según una dirección d y en un sentido dado es un punto | + | La translación de un punto <math>A</math> una magnitud <math>m</math>, según una dirección <math>d \ </math> y en un sentido dado es un punto <math>A'</math> tal que : <math>AA' = m;</math> <math>AA'</math> es paralelo a <math>d \ </math> e indica el sentido dado. |
| + | |||
| + | [[Imagen:27Translaciones.gif]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Homología
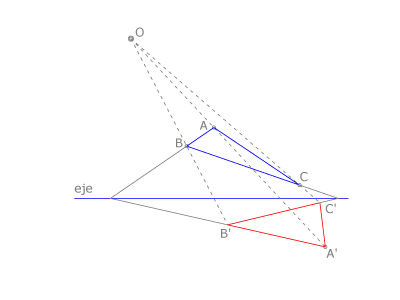
La homología es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras.
Transforma los puntos del plano: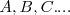 
en puntos del plano 
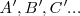, de modo que:
dos puntos homólogos 
y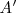 
están alineados con un punto fijo ![O \](/images/math/math-234a0c47337f83f676a1cb3a2a9cbcf0.png "O \")
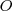que es el centro de la homología; dos rectas homólogas 
y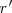 
se cortan en una recta doble llamada eje de la homología; existe un coeficiente de homología, 
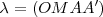, la razón doble en la que 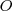es el centro, y 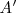un par de homólogos y 
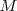el punto doble de la recta 
.
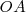Homotecia
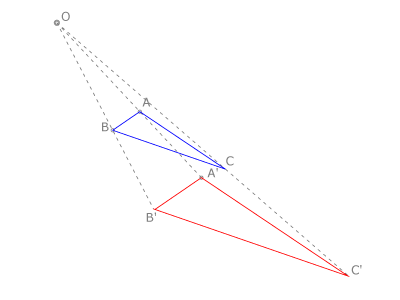
Es una homología con el eje en el infinito.
La homotecia es una transformación isomórfica y no isométrica, pues mantiene la forma de la figura que transforma, pero no su tamaño.
Transforma los puntos del plano: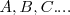
en puntos del plano 
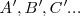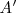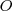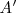, de modo que:dos puntos homólogos y están alineados con un punto fijo que es el centro de la homotecia; la razón entre las distancias de y a 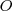es constante: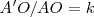 
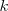se llama razón de la homotecia.
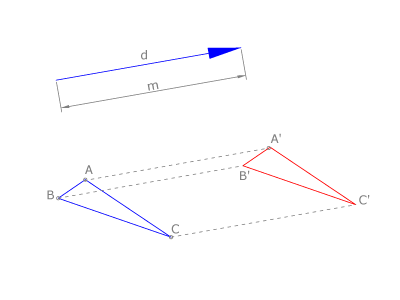
Afinidad
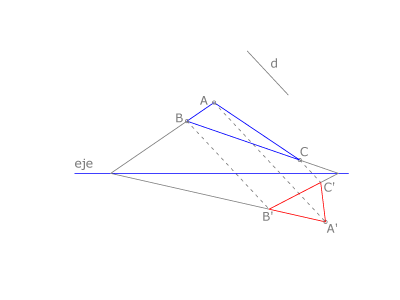
La afinidad es una homología con el centro en el infinito. Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de la figura que transforma.
Transforma los puntos del plano: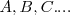 
en puntos del plano 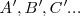, de modo que: dos puntos homólogos y 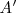definen un segmento paralelo a la dirección de afinidad ![d \](/images/math/math-0ed63a3352f81c497e8cdad53755377b.png "d \")
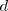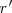; dos rectas homólogas y se cortan en una recta doble llamada 
, eje de la afinidad; existe un coeficiente de afinidad,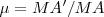 
, la razón en la que y 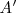son un par de homólogos y 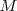el punto doble de la recta 
.
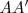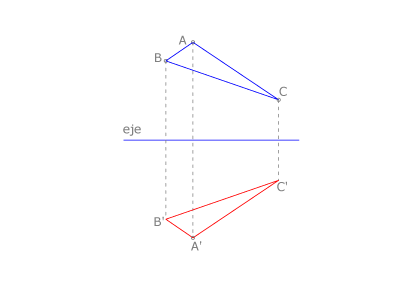
Simetrías
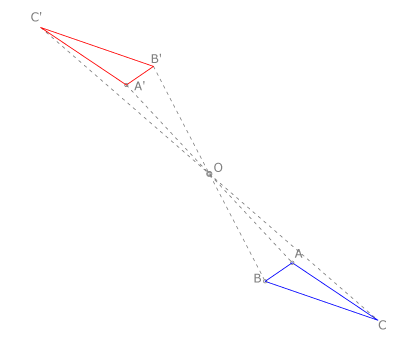
Las simetrías son isomórficas e isométricas, pues mantienen la forma y el tamaño de las figuras. En el plano existen dos tipos de simetrías: la central y la axial.
La simetría central de un punto respecto del centro 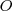es el punto 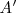, alineado con y 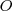, de modo que 
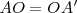. La simetría central es una homotecia con 
.
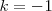La simetría axial de un punto respecto del eje e es el punto 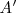, siendo la recta 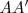perpendicular al eje y y 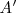equidistantes del mismo.
La simetría axial es una afinidad con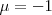 
Translaciones
Las translaciones son isomórficas e isométricas. Son homologías con el eje y el centro en el infinito.
La translación de un punto una magnitud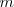 
, según una dirección 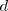y en un sentido dado es un punto 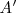tal que :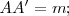 
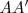es paralelo a 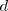e indica el sentido dado.
