Navegación
Proporcionalidad inversa
De Wikillerato
| (5 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | {{en desarrollo}} | ||
| + | |||
===Características generales=== | ===Características generales=== | ||
| - | Consideramos que una variable x puede adquirir los valores a,b,c,d,... y otra variable y los valores | + | Consideramos que una variable x puede adquirir los valores <math>a, b, c, d, ...</math> y otra variable y los valores <math>a' ,b' ,c' ,d' , ...</math> <math>x</math> e <math>y</math> son inversamente proporcionales si <math>a \cdot a' = b \cdot b' = c \cdot c' = d \cdot d' ... </math> |
===Teorema de Euclides=== | ===Teorema de Euclides=== | ||
El teorema de Euclides tiene dos enunciados que se conocen como teorema de la altura y teorema del cateto. | El teorema de Euclides tiene dos enunciados que se conocen como teorema de la altura y teorema del cateto. | ||
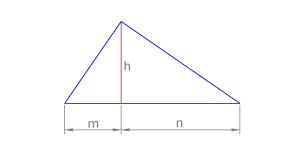
| - | Teorema de la altura:”la altura h de un triángulo rectángulo con respecto a su hipotenusa es la media proporcional de los dos segmentos, m y n, que el pie de h define en la hipotenusa: h = | + | Teorema de la altura:”la altura <math>h</math> de un triángulo rectángulo con respecto a su hipotenusa es la media proporcional de los dos segmentos, <math>m</math> y <math>n</math>, que el pie de <math>h</math> define en la hipotenusa: <math>h = \sqrt {m \cdot n}</math> |
| - | Teorema del cateto: “el cateto c de un triángulo rectángulo es la media proporcional de la hipotenusa a y | + | |
| + | [[Imagen:28TeoremadeEuclides.gif]] | ||
| + | |||
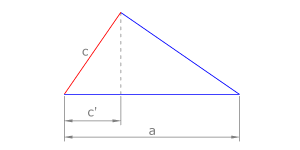
| + | Teorema del cateto: “el cateto <math>c</math> de un triángulo rectángulo es la media proporcional de la hipotenusa <math>a</math> y <math>c'</math>, proyección de <math>c</math> sobre ella: <math>c = \sqrt {c' \cdot a}</math> ” | ||
| + | |||
| + | [[Imagen:29TeoremadeEuclides.gif]] | ||
===Potencia=== | ===Potencia=== | ||
| - | Consideramos un punto P y una circunferencia c, de centro C. Trazamos rectas secantes a c que pasen por P. Estas rectas definen en c los puntos A,B,D,E,F,G. Se llama potencia del punto P respecto de la circunferencia c y se nota | + | |
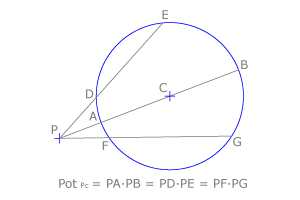
| + | Consideramos un punto <math>P</math> y una circunferencia <math>c</math>, de centro <math>C</math>. Trazamos rectas secantes a <math>c</math> que pasen por <math>P</math>. Estas rectas definen en <math>c</math> los puntos <math>A, B, D, E, F, G</math>. Se llama potencia del punto <math>P</math> respecto de la circunferencia <math>c</math> y se nota <math>Pot_{Pc}</math> al producto: <math>Pot_{Pc} = PA \cdot PB = PD \cdot PE= PF \cdot PG</math> | ||
| + | |||
| + | |||
La potencia es un caso de proporcionalidad inversa. | La potencia es un caso de proporcionalidad inversa. | ||
| + | |||
| + | [[Imagen:30Potencia.gif]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Características generales
Consideramos que una variable x puede adquirir los valores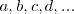 
y otra variable y los valores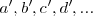 
e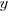 
son inversamente proporcionales si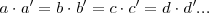 
Teorema de Euclides
El teorema de Euclides tiene dos enunciados que se conocen como teorema de la altura y teorema del cateto.
Teorema de la altura:”la altura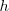 
de un triángulo rectángulo con respecto a su hipotenusa es la media proporcional de los dos segmentos, 
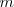y 
, que el pie de 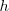define en la hipotenusa: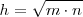 
Teorema del cateto: “el cateto 
de un triángulo rectángulo es la media proporcional de la hipotenusa 
y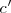 
, proyección de sobre ella: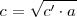 
”
Potencia
Consideramos un punto 
y una circunferencia , de centro 
. Trazamos rectas secantes a que pasen por . Estas rectas definen en los puntos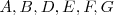 
. Se llama potencia del punto respecto de la circunferencia y se nota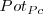 
al producto: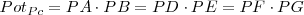 
La potencia es un caso de proporcionalidad inversa.
