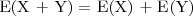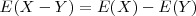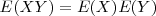Esperanza matemática
De Wikillerato
| (5 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | Sea <math>X</math> una variable aleatoria, el "Valor Esperado" o "Esperanza Matemática" de dicha variable es el número representado como <math>E[X]</math> y que formaliza la idea de valor medio de un fenómeno aleatorio. | |
| - | <math>X</math> | + | |
| - | + | ||
| - | + | ---- | |
| + | '''Caso discreto''' | ||
| + | |||
| + | En caso que <math>X</math> sea una variable aleatoria discreta con valores <math>x_{1}, x_{2}, ..., x_{n}</math> y sus probabilidades estén representadas por la función discreta de probabilidad <math>p(x_{1}), p(x_{2}), ..., p(x_{n})</math>, la esperanza se calcula como: | ||
| + | |||
| + | |||
| + | <math>E[X] = x_{1} p( x_{1} ) + x_{2} p( x_{2} ) + ... + x_{n} p( x_{n} ) = \sum_{i=1}^{n} x_{i} p(x_{i}) </math> | ||
| + | |||
| + | |||
| + | ---- | ||
| + | '''Caso continuo''' | ||
| + | |||
| + | En caso en que <math>X</math> sea una variable aleatoria continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad <math>f(x)</math>: | ||
| + | |||
| + | |||
| + | <math>E[X] = \int_{\infty}^{-\infty} x f(x) dx</math> | ||
| + | |||
== Propiedades de la Esperanza:== | == Propiedades de la Esperanza:== | ||
| - | |||
| - | |||
| - | |||
| - | E(X + Y) = E(X) + E(Y) | + | Para poder operar con la esperanza debemos conocer sus propiedades. Sean <math>X</math> e <math>Y</math> dos variables aleatorias, y <math>c</math> una constante, se pueden aplicar las siguientes operaciones: |
| + | |||
| + | * <math>E[c] = c</math> | ||
| + | |||
| + | * <math>E[cX] = cE[X]</math> | ||
| + | |||
| + | * <math>$E(X + Y) = E(X) + E(Y)$</math> | ||
| + | |||
| + | * <math> E(X - Y) = E(X) - E(Y)</math> | ||
| + | |||
| + | * <math> E(XY) = E(X) E(Y)</math> | ||
| + | |||
| + | |||
| + | == Ejemplo:== | ||
| - | + | Representemos con <math>X</math> la variable aleatoria que representa una tirada con un dado de 6 caras. Los posibles valores de <math>X</math> son <math>1, 2, 3, 4, 5, </math> y <math>6</math> todos ellos con la misma probalibilidad <math>\frac{1}{6}</math>, la esperanza de <math>X</math> es: | |
| - | E | + | <math>E[X] = 1\cdot\frac{1}{6} + 2\cdot\frac{1}{6} + 3\cdot\frac{1}{6} + 4\cdot\frac{1}{6} + 5\cdot\frac{1}{6} + 6\cdot\frac{1}{6} = 3.5</math> |
| - | + | [[Categoría:Matemáticas]] | |
Revisión actual
Sea 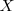 una variable aleatoria, el "Valor Esperado" o "Esperanza Matemática" de dicha variable es el número representado como
una variable aleatoria, el "Valor Esperado" o "Esperanza Matemática" de dicha variable es el número representado como ![E[X] E[X]](/images/math/math-44d1a318082b09db3efb8767c25e8043.png) y que formaliza la idea de valor medio de un fenómeno aleatorio.
y que formaliza la idea de valor medio de un fenómeno aleatorio.
Caso discreto
En caso que 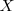 sea una variable aleatoria discreta con valores
sea una variable aleatoria discreta con valores 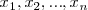 y sus probabilidades estén representadas por la función discreta de probabilidad
y sus probabilidades estén representadas por la función discreta de probabilidad 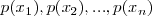 , la esperanza se calcula como:
, la esperanza se calcula como:
![E[X] = x_{1} p( x_{1} ) + x_{2} p( x_{2} ) + ... + x_{n} p( x_{n} ) = \sum_{i=1}^{n} x_{i} p(x_{i}) E[X] = x_{1} p( x_{1} ) + x_{2} p( x_{2} ) + ... + x_{n} p( x_{n} ) = \sum_{i=1}^{n} x_{i} p(x_{i})](/images/math/math-64fae95964ef1eedc7d1082c2698e2e7.png)
Caso continuo
En caso en que 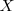 sea una variable aleatoria continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad
sea una variable aleatoria continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad 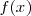 :
:
![E[X] = \int_{\infty}^{-\infty} x f(x) dx E[X] = \int_{\infty}^{-\infty} x f(x) dx](/images/math/math-0a57975c9369e480470e96ae154b4ffc.png)
Propiedades de la Esperanza:
Para poder operar con la esperanza debemos conocer sus propiedades. Sean 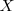 e
e 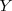 dos variables aleatorias, y
dos variables aleatorias, y  una constante, se pueden aplicar las siguientes operaciones:
una constante, se pueden aplicar las siguientes operaciones:
Ejemplo:
Representemos con 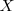 la variable aleatoria que representa una tirada con un dado de 6 caras. Los posibles valores de
la variable aleatoria que representa una tirada con un dado de 6 caras. Los posibles valores de 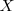 son
son 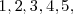 y
y 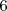 todos ellos con la misma probalibilidad
todos ellos con la misma probalibilidad  , la esperanza de
, la esperanza de 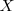 es:
es:
![E[X] = 1\cdot\frac{1}{6} + 2\cdot\frac{1}{6} + 3\cdot\frac{1}{6} + 4\cdot\frac{1}{6} + 5\cdot\frac{1}{6} + 6\cdot\frac{1}{6} = 3.5 E[X] = 1\cdot\frac{1}{6} + 2\cdot\frac{1}{6} + 3\cdot\frac{1}{6} + 4\cdot\frac{1}{6} + 5\cdot\frac{1}{6} + 6\cdot\frac{1}{6} = 3.5](/images/math/math-3f6a6b109ad65e509adaeb7d972240cd.png)


![E[c] = c E[c] = c](/images/math/math-85b6119359747b2b702ddeec9aa97eed.png)
![E[cX] = cE[X] E[cX] = cE[X]](/images/math/math-b7f81e3a2a99ee4815b0c6ffa99bbf25.png)