Navegación
Transformación basada en la proporcionalidad inversa
De Wikillerato
(Diferencias entre revisiones)
(→Inversión) |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 1: | Línea 1: | ||
| + | {{en desarrollo}} | ||
| + | |||
===Inversión=== | ===Inversión=== | ||
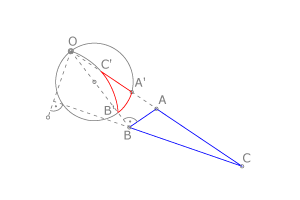
Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras. | Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras. | ||
Transforma los puntos del plano: <math>A, B, C....</math> en puntos del plano <math>A' ,B' ,C'...</math>, de modo que: | Transforma los puntos del plano: <math>A, B, C....</math> en puntos del plano <math>A' ,B' ,C'...</math>, de modo que: | ||
| - | dos puntos inversos <math>A</math> y <math>A'</math> están alineados con un punto fijo <math>O \ </math> que es el centro de inversión; <math>OA \cdot OA' = k =</math> potencia de inversión. | + | dos puntos inversos <math>A</math> y <math>A'</math> están alineados con un punto fijo <math>O \ </math> que es el centro de [[Inversión (Dibujo)|inversión]]; <math>OA \cdot OA' = k =</math> potencia de inversión. |
[[Imagen:31TransformacionProporcionalidadInversa.gif]] | [[Imagen:31TransformacionProporcionalidadInversa.gif]] | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión actual
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Inversión
Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras.
Transforma los puntos del plano: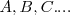 
en puntos del plano 
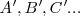, de modo que:
dos puntos inversos 
y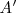 
están alineados con un punto fijo ![O \](/images/math/math-234a0c47337f83f676a1cb3a2a9cbcf0.png "O \")
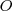que es el centro de inversión; 
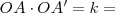potencia de inversión.
