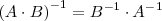De Wikillerato
(Diferencias entre revisiones)
|
|
| Línea 85: |
Línea 85: |
| | | | |
| | | | |
| - | Para calcular la matriz inversa de una matriz regular podemos utilizar dos procedimientos:
| |
| - |
| |
| - | <br/>
| |
| | | | |
| | ===Mediante la definicion=== | | ===Mediante la definicion=== |
| Línea 103: |
Línea 100: |
| | \begin{array}[c]{cc} | | \begin{array}[c]{cc} |
| | 1 & 2 | | 1 & 2 |
| - | \\
| |
| - | 3 & 7
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | hacemos
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A^{-1} =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a & b</math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | como
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | I = A \cdot A^{-1} \Rightarrow
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 2
| |
| - | \\
| |
| - | 3 & 7
| |
| - | \end{array}
| |
| - | \right)
| |
| - | \cdot
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a & b
| |
| - | \\
| |
| - | c & d
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 0
| |
| - | \\
| |
| - | 0 & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Operando:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a + 2c & b + 2d
| |
| - | \\
| |
| - | 3a + 7c & 3b + 7d
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 0
| |
| - | \\
| |
| - | 0 & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | \Leftrightarrow
| |
| - | \left\{
| |
| - | \begin{array}[c]{ccc}
| |
| - | a + 2c & = & 1
| |
| - | \\
| |
| - | 3a + 7c & = & 0
| |
| - | \\
| |
| - | b + 2d & = & 0
| |
| - | \\
| |
| - | 3b + 7d & = & 1
| |
| - | \\
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \Rightarrow \left\{
| |
| - | \begin{array}[c]{ccc}
| |
| - | a & = & 7
| |
| - | \\
| |
| - | b & = & -2
| |
| - | \\
| |
| - | c & = & -3
| |
| - | \\
| |
| - | d & = & 1
| |
| - | \\
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ===Método de Gauss-Jordan===
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | La inversa de una matriz regular
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - | se calcular transformando la matriz
| |
| - | <math>
| |
| - | \left(
| |
| - | \, A \, \left| \, I \, \right.
| |
| - | \right)
| |
| - | </math>
| |
| - | mediante operaciones
| |
| - | elementales por filas en la matriz
| |
| - | <math>
| |
| - | \left(
| |
| - | \, I \, \left| \, A^{-1} \, \right.
| |
| - | \right)
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Operaciones elementales por filas en una matriz====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las operaciones elementales por filas en una matriz son las siguientes:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 1. Intercambiar las filas
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | j,
| |
| - | </math>
| |
| - | que designaremos por
| |
| - | <math>
| |
| - | F_i \longrightarrow F_j
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 2. Multiplicar la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | por el numero
| |
| - | <math>
| |
| - | k \neq 0
| |
| - | </math>
| |
| - | y sustituirla por el resultado; lo designamos por
| |
| - | <math>
| |
| - | F_i \to k \cdot F_i
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 3. Sumar la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | con la fila
| |
| - | <math>
| |
| - | j
| |
| - | </math>
| |
| - | y sustituirla por el resultado; lo designamos por
| |
| - | <math>
| |
| - | F_i \to \ F_i + F_j
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 4. Sumar las filas
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | j,
| |
| - | </math>
| |
| - | , multiplicadas por sendos números, y llevar el resultado a la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | o
| |
| - | <math>
| |
| - | j
| |
| - | </math>
| |
| - | . Lo designamos por
| |
| - | <math>
| |
| - | F_i
| |
| - | </math>
| |
| - | o
| |
| - | <math>
| |
| - | F_j \to k \cdot F_i + t \cdot F_j
| |
| - | </math>
| |
| | | | |
| | ==Ejercicios resueltos== | | ==Ejercicios resueltos== |
Revisión de 22:41 3 nov 2008
Definición
La matriz inversa de una matriz cuadrada
 de orden
de orden
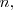 es la matriz,
es la matriz,
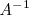 , de orden
, de orden
 que verifica:
que verifica:
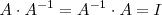
donde
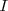 es la matriz identidad de orden
es la matriz identidad de orden
 .
.
Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices
singulares.
Las propiedades más importantes relativas a la matriz inversa:
1. Si existe,
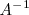 es única.
es única.
2.
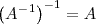
3.
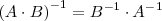
Cálculo de la matriz inversa
Mediante la definicion
Ejemplo
[Unparseable or potentially dangerous latex formula. Error 3 ]
 de orden
de orden
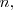 es la matriz,
es la matriz,
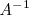 , de orden
, de orden
 que verifica:
que verifica:
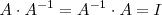
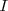 es la matriz identidad de orden
es la matriz identidad de orden
 .
.
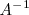 es única.
es única.