Postulados de Bohr
De Wikillerato
| Línea 56: | Línea 56: | ||
Las órbitas estacionarias admisibles son aquellas en las que el '''momento angular orbital''' <math>L</math> del electrón está cuantizado, pudiendo este asumir solamente valores múltiplos enteros de <math>\frac {h} {2\pi }</math>, donde <math>h</math> es la constante de Planck y <math>n</math> es un número integral (<math>n=1,2,3...</math>), llamado ''numero cuántico principal''. Así, | Las órbitas estacionarias admisibles son aquellas en las que el '''momento angular orbital''' <math>L</math> del electrón está cuantizado, pudiendo este asumir solamente valores múltiplos enteros de <math>\frac {h} {2\pi }</math>, donde <math>h</math> es la constante de Planck y <math>n</math> es un número integral (<math>n=1,2,3...</math>), llamado ''numero cuántico principal''. Así, | ||
| - | <math>L=n\frac{h}{2\pi}</math> | + | <math>L=n\frac{h}{2\pi}</math> <math>[4]</math> |
Este postulado Bohr introduce de nuevo la idea de cuantización en una nueva área de la física clásica al presuponer la idea de cuantización del momento angular orbital de un electrón que se mueve bajo la acción de una fuerza culombinana. | Este postulado Bohr introduce de nuevo la idea de cuantización en una nueva área de la física clásica al presuponer la idea de cuantización del momento angular orbital de un electrón que se mueve bajo la acción de una fuerza culombinana. | ||
<h4>Órbitas y espectro energético del átomo de Bohr</h4> | <h4>Órbitas y espectro energético del átomo de Bohr</h4> | ||
| + | |||
| + | Utilizando estos postulado Bohr fue capaz de calcular el tamaño de las órbitas estacionarias y de la energía de esas órbitas, veamos como: | ||
| + | |||
| + | Teniendo en cuenta como habíamos visto la electrodinámica clásica, si la carga nuclear es <math>+Ze</math> y la carga del electrón -e la fuerza centrípeta necesaría para mover el electrón en un órbita circular es proporcionada por la ley de Coulomb | ||
| + | |||
| + | <math>\frac{kZe^2}{r}</math> | ||
| + | |||
| + | <math>F=\frac{kZe^2}{r^2}=\frac{mv^2}{r} </math> despejando de esta ecuación para la velocidad orbital del electrón <math<v></math> tenemos que: | ||
| + | |||
| + | <math>v=(\frac{kZe^2}{mr})1/2}</math> <math>[5]</math> | ||
| + | |||
| + | La condición de cuantificación del momento angular orbital L de Bohr (tercer postulado) para el elctrón es: | ||
| + | |||
| + | <math>L=mvr=\frac{nh}{2\pi}=n\hbar</math> <math>n=1,2,3....</math> <math>[6]</math> | ||
| + | |||
| + | la constante <math>\hbar</math>, llamada h barrada o constante de Planck reducida :<math> \hbar=\frac{h}{2\pi}</math>, es frecuente más conveniente utilizarla en vez de <math>h</math> en los cálculos. Al igual que la frecuencia angular <math>\omega=2 \pi\nu</math> es frecuentemente más conveniente que <math>\nu</math> estando expresada en radianes por segundo (rad/s) en lugar de ciclos por segundo (Hz). Una frecuencia expresada en radianes por segundo es referida como una frecuencia <math>\omega</math> angular por lo que la '''ecuación de Planck''' puede también expresarse como: <math>E=\hbar\omega</math> <math>[7]>/math> | ||
| + | |||
| + | La combinación de las ecuaciones <math>[ 5]</math> y <math>[6]</math> permite escribir: | ||
| + | |||
| + | <math>r=\frac{n\hbar}{{mv}</math>=<math>\frac{n\hbar}{m}</math><math>(\frac{rm}{kZe^2})^{1/2}</math> <math>[8]</math> | ||
| + | |||
| + | Elevando al cuadrado los dos lados de la ecuación <math>[8</math>] tenemos: | ||
| + | |||
| + | <math>r^2=\frac{n^2\hbar^2}{m^2} </math><math>(\frac{rm}{kZe^2})</math> <math>[9]<math> | ||
| + | |||
| + | Cancelando las cantidades comunes a ambos lados nos queda: | ||
| + | |||
| + | <math>r(n)=\frac{n^2\hbar^2}{mZe^2}=\frac{n^2aº}{Z}</math> <math>[10]<math> | ||
| + | |||
| + | donde <math>r(n)</math> es el radio de la órbita electrónica que depende de <math>n</math> el número cuántico principal, y donde: | ||
| + | |||
| + | <math>aº=\frac{\hbar^2}{mke^2}=0.529 Å=0.0529 nanómetros (nm)>/math> | ||
| + | |||
| + | es llamado '''radio de Bohr'''. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<h4>Fallos del modelo atómico de Bohr</h4> | <h4>Fallos del modelo atómico de Bohr</h4> | ||
Revisión de 11:56 27 nov 2008
El físico danes Niels H. D. Bohr (1885-1962) propuso un modelo en 1913 publicado en la revista Philosophical Magazine para el átomo de hidrógeno en el que combinaba el trabajo de Planck, Einstein y Rutherford y que tubo un éxito muy destacado en predecir el ciertas características del espectro de hidrógeno observadas experimentalmente.
Antecedentes históricos a la propuesta de Bohr
El modelo atómico planetario propuesto en 1911 por el físico neozelandés Ernest Rutherford (1871-1937) en base a los experimentos de borbamdeando de finas láminas de átomos de oro con partículas 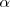 (núcleos de átomos de helio) que los científicos alemanes Hans W. Geiger (1882-1945) y sir Ernest Marsden (1889-1970) habían realizaron en bajo su dirección (entonces eran sus alumnos), suponía la existencia en el átomo de un núcleo de pequeño tamaño (~[Unparseable or potentially dangerous latex formula. Error 3 ]) y volumen en relación con el resto del átomo completo ([Unparseable or potentially dangerous latex formula. Error 3 ]) donde se concentra la mayoría de la masa atómica, estando cargado positivamente y con los electrones de carga negativa orbitando (girando) alrededor del mismo unidos por la atracción electrostática del núcleo, al igual que los planetas que orbitan alrededor del Sol.
(núcleos de átomos de helio) que los científicos alemanes Hans W. Geiger (1882-1945) y sir Ernest Marsden (1889-1970) habían realizaron en bajo su dirección (entonces eran sus alumnos), suponía la existencia en el átomo de un núcleo de pequeño tamaño (~[Unparseable or potentially dangerous latex formula. Error 3 ]) y volumen en relación con el resto del átomo completo ([Unparseable or potentially dangerous latex formula. Error 3 ]) donde se concentra la mayoría de la masa atómica, estando cargado positivamente y con los electrones de carga negativa orbitando (girando) alrededor del mismo unidos por la atracción electrostática del núcleo, al igual que los planetas que orbitan alrededor del Sol.
La mecánica clásica permitía un modelo de órbitas circulares y elípticas para el electrón en este modelo planetario. Por ejemplo, el átomo más sencillo de todos, el átomo de hidrógeno, constaría de un electrón y un núcleo positivo (con un protón) la carga del núcleo 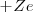 es la misma que la del electrón (
es la misma que la del electrón (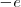 ) pero de signo contrario, por lo que el átomo es eléctricamente neutro. Este modelo planetario es estable mecánicamente, debido a que el potencial de Coulomb:
) pero de signo contrario, por lo que el átomo es eléctricamente neutro. Este modelo planetario es estable mecánicamente, debido a que el potencial de Coulomb:
[Unparseable or potentially dangerous latex formula. Error 3 ] ![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png)
proporciona la fuerza centrípeta:
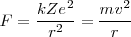
![[2] [2]](/images/math/math-ec736101c15bd1d1133c7e3d7015ddd9.png)
necesaria para que el electrón se mueva en un circulo de radio  a una velocidad
a una velocidad  , siendo
, siendo 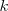 la constante de Coulomb. Pero es eléctricamente inestable debido a que el electrón está siempre acelerando hacia el centro del círculo. Las leyes de la electrodinámica clásica (ley de Larmor) predicen que una carga acelerando radia luz con una frecuencia igual al periodo del movimiento, en este caso la frecuencia de revolución
la constante de Coulomb. Pero es eléctricamente inestable debido a que el electrón está siempre acelerando hacia el centro del círculo. Las leyes de la electrodinámica clásica (ley de Larmor) predicen que una carga acelerando radia luz con una frecuencia igual al periodo del movimiento, en este caso la frecuencia de revolución  .
.
Así clasicamente tenemos que:
[Unparseable or potentially dangerous latex formula. Error 3 ]=[Unparseable or potentially dangerous latex formula. Error 3 ]~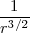
![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png)
La energía total del electrón es la suma de ls energías cinética y potencial:
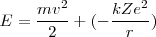
![[4] [4]](/images/math/math-b89757a59b41b6506218bd6647cd5ee7.png)
A partir de la ecuación ![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png) se tiene que
se tiene que 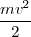 =
=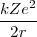 (un resultado que se mantiene para el movimiento circular [[1]] en un campo de fuerzas iversamente proporcional al cuadrado de la distancia), así que la energía total puede ser descrita como:
(un resultado que se mantiene para el movimiento circular [[1]] en un campo de fuerzas iversamente proporcional al cuadrado de la distancia), así que la energía total puede ser descrita como:
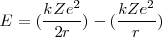 =
= 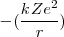 ~
~ 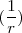
![[5] [5]](/images/math/math-311713d7e899562efc3b7c08c8a01ccb.png)
Así, la física clásica predice que debido a que la energía es perdida por radiación el tamaño de la órbita del electrón alrededor del núcleo (dado por  ) se irá reduciendo cada vez más haciéndose cada vez más pequeña, incrementándose de igual manera la tasa en la cual la energía del electrón es perdida, el proceso que terminaría cuando el electrón alcanzara el núcleo, colapsando con el mismo. Este tiempo puede ser calculado por la mecánica y electrodinámica clásica y resultaría ser menos de un microsegundo. Así, el modelo planetario clásico para el átomo predice que este debería radiar un espectro continuo (ya que la frecuencia de revolución cambia continuamente cuando el electrón cae en espiral hacia el núcleo) y que se produciría un colapso cuando el electrón se precipitara contra el núcleo, un resultado que afortunadamente no ocurre. Es decir según este modelo el átomo es una entidad inestable, llamada a desaparecer con el tiempo. Experimentalmente se comprueba todo lo contrario que a no ser que el átomo sea excitado, el átomo no radia, no emite radiación electromagnética y que cuando es excitado el átomo radia una línea espectral discreta y no un espectro de radiación continua.
) se irá reduciendo cada vez más haciéndose cada vez más pequeña, incrementándose de igual manera la tasa en la cual la energía del electrón es perdida, el proceso que terminaría cuando el electrón alcanzara el núcleo, colapsando con el mismo. Este tiempo puede ser calculado por la mecánica y electrodinámica clásica y resultaría ser menos de un microsegundo. Así, el modelo planetario clásico para el átomo predice que este debería radiar un espectro continuo (ya que la frecuencia de revolución cambia continuamente cuando el electrón cae en espiral hacia el núcleo) y que se produciría un colapso cuando el electrón se precipitara contra el núcleo, un resultado que afortunadamente no ocurre. Es decir según este modelo el átomo es una entidad inestable, llamada a desaparecer con el tiempo. Experimentalmente se comprueba todo lo contrario que a no ser que el átomo sea excitado, el átomo no radia, no emite radiación electromagnética y que cuando es excitado el átomo radia una línea espectral discreta y no un espectro de radiación continua.
Para “solucionar” estas dificultades inabordables desde un punto de vista clásico, Bohr introdujo ad hoc en su modelo de 1913 una serie de postulados no clásicos de naturaleza cuántica, introduciendo con ello la cuantificación (cuantización) iniciada por Planck y Einstein en el “corazón” de la estructura del átomo.
Postulados del modelo atómico de Bohr
Primer postulado:
Los electrones se mueven en ciertas órbitas permitidas alrededor del núcleo sin emitir radiación. Así Bohr asumió que el átomo de hidrógeno puede existir solo en ciertos estados discretos, los cuales son denominados estados estacionarios del átomo. En el átomo no hay emisión de radiación electromagnética mientras el electrón no cambia de órbita.
Con este postulado Bohr evitaba el problema de la inestabiliad orbital eléctrica del electrón que predice la electrodinámica clásica y por tanto del átomo, al postular que la radiación de energía por parte de las partículas cargadas es válida a escala macroscópica pero no es aplicable al mundo microscópico del átomo, pero si esto es así surge el problema de de explicar la transición entre los estados estacionarios y la emisión de radiación por el átomo para ello Borh introdujo otro postulado :
Segundo postulado:
El átomo radia cuando el electrón hace una transición (“salto”) desde un estado estacionario a otro, es decir toda emisión o absorción de radiación entre un sistema atómico esta generada por la transición entre dos estados estacionarios. La radiación emitida (o absorbida) durante la transición corresponde a un cuanto de energía (fotón) cuya frecuencia  esta relacionada con las energías de las órbitas estacionarias por la ecuación de Planck:
esta relacionada con las energías de las órbitas estacionarias por la ecuación de Planck: 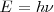
y está determinada por la relación :
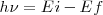
![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png)
donde 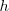 es la constante de Planck (
es la constante de Planck (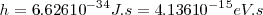 ), con
), con 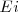 y
y 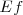 son las energías de los estados estacionarios iniciales y finales de la transición electrónica. La ecuación
son las energías de los estados estacionarios iniciales y finales de la transición electrónica. La ecuación ![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png) es referida como la condición de frecuencia de Bohr.
es referida como la condición de frecuencia de Bohr.
Este postulado está basado en el concepto de fotón introducido por Einstein [[2]], junto con la conservación de la energía; si la luz está compuesta de fotones de energía , la emisión por parte del átomo de un fotón debe suponer una pérdida de energía igual a la energía del fotón emitido (o si es la absorción de un fotón a la ganancia de energía), por lo tanto es un postulado equivalente aquel de la conservación de la energía con la emisión del fotón, es crucial, debido a que con el Bohr se desvía “de la senda de la teoría clásica”, que requiere que la frecuencia de radiación sea igual a la frecuencia del movimiento de la partícula cargada. Así, mientras el equilibrio dinámico mecánico del sistema en los estados estacionarios está regido por las leyes ordinarias de la mecánica, sin embargo, dichas leyes no son aplicables cuando se trata de transiciones entre estados estacionarios.
Tercer postulado:
Las órbitas estacionarias admisibles son aquellas en las que el momento angular orbital 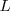 del electrón está cuantizado, pudiendo este asumir solamente valores múltiplos enteros de
del electrón está cuantizado, pudiendo este asumir solamente valores múltiplos enteros de 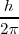 , donde
, donde 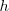 es la constante de Planck y
es la constante de Planck y  es un número integral (
es un número integral (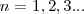 ), llamado numero cuántico principal. Así,
), llamado numero cuántico principal. Así,
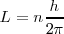
![[4] [4]](/images/math/math-b89757a59b41b6506218bd6647cd5ee7.png)
Este postulado Bohr introduce de nuevo la idea de cuantización en una nueva área de la física clásica al presuponer la idea de cuantización del momento angular orbital de un electrón que se mueve bajo la acción de una fuerza culombinana.
Órbitas y espectro energético del átomo de Bohr
Utilizando estos postulado Bohr fue capaz de calcular el tamaño de las órbitas estacionarias y de la energía de esas órbitas, veamos como:
Teniendo en cuenta como habíamos visto la electrodinámica clásica, si la carga nuclear es 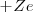 y la carga del electrón -e la fuerza centrípeta necesaría para mover el electrón en un órbita circular es proporcionada por la ley de Coulomb
y la carga del electrón -e la fuerza centrípeta necesaría para mover el electrón en un órbita circular es proporcionada por la ley de Coulomb
[Unparseable or potentially dangerous latex formula. Error 3 ]
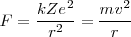 despejando de esta ecuación para la velocidad orbital del electrón <math<v></math> tenemos que:
despejando de esta ecuación para la velocidad orbital del electrón <math<v></math> tenemos que:
[Unparseable or potentially dangerous latex formula. Error 3 ] ![[5] [5]](/images/math/math-311713d7e899562efc3b7c08c8a01ccb.png)
La condición de cuantificación del momento angular orbital L de Bohr (tercer postulado) para el elctrón es:
[Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ] ![[6] [6]](/images/math/math-efa651c624c49f90c998fb329daf1ea9.png)
la constante 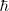 , llamada h barrada o constante de Planck reducida :
, llamada h barrada o constante de Planck reducida :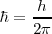 , es frecuente más conveniente utilizarla en vez de
, es frecuente más conveniente utilizarla en vez de 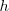 en los cálculos. Al igual que la frecuencia angular
en los cálculos. Al igual que la frecuencia angular 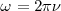 es frecuentemente más conveniente que
es frecuentemente más conveniente que  estando expresada en radianes por segundo (rad/s) en lugar de ciclos por segundo (Hz). Una frecuencia expresada en radianes por segundo es referida como una frecuencia
estando expresada en radianes por segundo (rad/s) en lugar de ciclos por segundo (Hz). Una frecuencia expresada en radianes por segundo es referida como una frecuencia 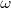 angular por lo que la ecuación de Planck puede también expresarse como:
angular por lo que la ecuación de Planck puede también expresarse como: 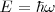 [Unparseable or potentially dangerous latex formula. Error 3 ] y
[Unparseable or potentially dangerous latex formula. Error 3 ] y ![[6] [6]](/images/math/math-efa651c624c49f90c998fb329daf1ea9.png) permite escribir:
permite escribir:
[Unparseable or potentially dangerous latex formula. Error 3 ]=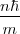
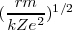
![[8] [8]](/images/math/math-041bd3d5f7775a49b25036b205a084f9.png)
Elevando al cuadrado los dos lados de la ecuación [Unparseable or potentially dangerous latex formula. Error 3 ]] tenemos:
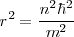
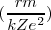 [Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ] es el radio de la órbita electrónica que depende de
[Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ] es el radio de la órbita electrónica que depende de  el número cuántico principal, y donde:
el número cuántico principal, y donde:
[Unparseable or potentially dangerous latex formula. Error 1 ]) los cálculos cuánticos deben estar de acuerdo con los cálculos clásicos o en otras palabras si se realizan modificaciones de la física clásica para describir el mundo submicroscópico cuando los resultadosde estos sean extendidos al mundo macroscópico, los resultados deben estar de acuerdo con las leyes clásicas de la física que han sido verificadas en la escala ordinaria del mundo de cada día.
Aunque los detalles del modelo atómico de Bohr han sido han sido suplantados por la moderna mecánica cuántica, su condición de frecuencia y el principio de correspondencia permanecen todavía como un rasgo esencial de la nueva teoría cuántica.
Referencias
Niels Bohr. La teoría atómica y la descripción de la Naturaleza.Alianza Editorial.1988. Un libro esencial para comprender el pensamiento de uno de los fundadores y más influyentes científicos de la física moderna.
Paul.A.Tipler & Ralph A. Lewellyn. Modern Physics.W.H. Freeman Company. New Tork Third Edition.1999. Un clásico de los libros de texto de física moderna
Enlaces externos
Artículo original de Bohr de 1913 publicado en la revista Philosophical Magazine en inglés:[[3]]
Hyperphysics: Bohr Model [[4]]
Tweet


