Propiedades de la integral definida
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | + | La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones: | |
| - | + | ||
| - | + | <br/> | |
| - | + | <center> | |
| - | + | <math> | |
| - | + | \int_a^b | |
| - | + | \left( | |
| - | + | \, \mathrm{f} \left( \, x \, \right) \, + \, | |
| - | + | \mathrm{g} \left( \, x \, \right) | |
| - | + | \right) | |
| - | + | \cdot \mathrm{d}x | |
| + | \, = \, | ||
| + | \int_a^b \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x \, + \, | ||
| + | \int_a^b \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| - | + | <br/> | |
| - | [[ | + | La integral indefinida del producto de un número real <math> k </math> por una función es igual al producto de <math> k </math> por la integral indefinida de la función: |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \int_a^b k \cdot \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x \, = \, | ||
| + | k \cdot \int_a^b \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para demostrar las ultimas dos igualdades basta con derivar los dos terminos en | ||
| + | ambas igualdades. | ||
| + | |||
| + | \x En una integral definida el limite superior de integraci\'on puede ser menor | ||
| + | que el limite inferior de integraci\'on y | ||
| + | <center> | ||
| + | <math> | ||
| + | \int_a^b \cdot \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x \, = \, | ||
| + | - \cdot \int_b^a \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | [[Category: Matemáticas]] | ||
Revisión de 10:21 12 dic 2010
La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones:
[Unparseable or potentially dangerous latex formula. Error 3 ]
La integral indefinida del producto de un número realpor una función es igual al producto de
por la integral indefinida de la función:
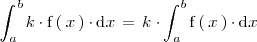
Para demostrar las ultimas dos igualdades basta con derivar los dos terminos en ambas igualdades.
\x En una integral definida el limite superior de integraci\'on puede ser menor que el limite inferior de integraci\'on y
[Unparseable or potentially dangerous latex formula. Error 3 ]



